1.3集合的基本运算课件 北师大必修1
文档属性
| 名称 | 1.3集合的基本运算课件 北师大必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 94.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-18 16:23:17 | ||
图片预览






文档简介
课件16张PPT。1.1.3 集合的基本运算一、并集可以发现:集合C是由属于集合A或属于集合B的元素组成的 考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
(1)A={1,3,5} B={2,4,6} C={1,2,3,4,5,6}
(2)A={x|x是有理数} B= {x|x是无理数}
C= {x|x是实数} 思考:实数有加法运算,类比实数的加法运算,集合是否也可以“相加”呢?1. 并集:由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集记作:A∪B 读作:“A并B”2. 并集的表示:
自然语言:由所有属于集合A或属于集合B的元素组成的集合,成为集合A与B的并集
符号语言: A∪B ={x | x∈A或x∈B}
图形语言:例1. 设A={4,5,6,8} , B={3,5,7,8}, 求A∪B 解:A∪B ={3,4,5,6,7,8} 注:求两个集合的并集时,它们的公共元素在并集中只能出现一次例2. 设集合A={x|-1 (1) A∪A=A (2) A∪?=A3. 并集的性质 (1) A∪A=A (2) A∪?=A
(3) A∪B=B∪A (4)
(5)若x∈A∪B, 则x∈A或x∈B
(6) A∪B=B二、交集 考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
(1)A={2,4,6,8,10} B={3,5,8,12} C={8}
(2)A={x|x是166中学的女同学}
B= {x|x是166中学高一年级同学}
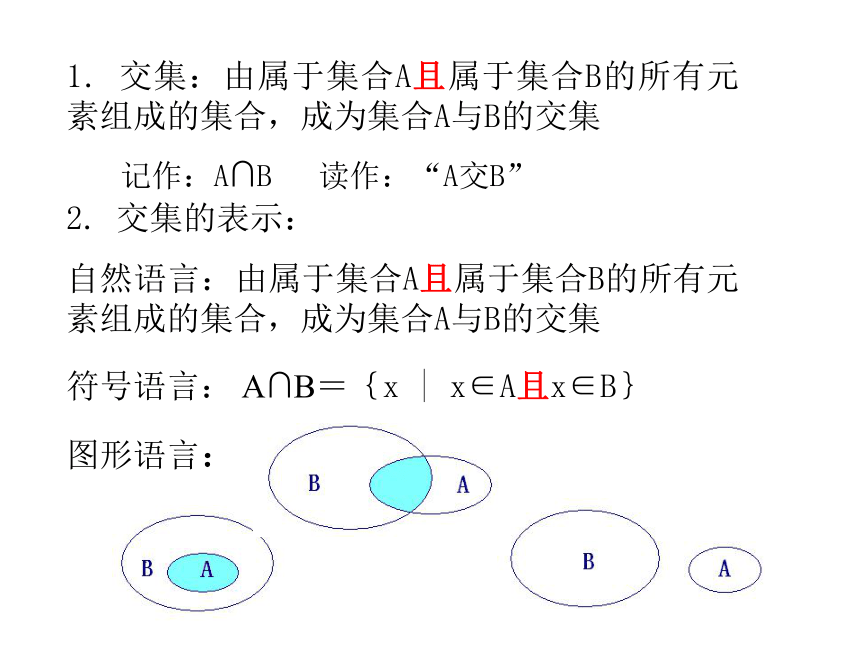
C= {x|x是166中学高一年级女同学} 可以发现:集合C是由那些既属于集合A又属于集合B的所有元素组成的1. 交集:由属于集合A且属于集合B的所有元素组成的集合,成为集合A与B的交集记作:A∩B 读作:“A交B”2. 交集的表示:
自然语言:由属于集合A且属于集合B的所有元素组成的集合,成为集合A与B的交集
符号语言: A∩B={x | x∈A且x∈B}
图形语言:例3. 166中学开运动会,设
A={x|x是166中高一年级参加百米赛跑的同学},
B={x|x是166中高一年级参加跳高比赛的同学},
求A∩B 解:A∩B ={x|x是166中高一年级既参加百米赛跑又参加跳高比赛的同学}解:平面内直线l1 、l2可能有三种位置关系:即相交于一点,平行或重合例4. 设平面内直线l1 上点的集合为L1 ,直线l2上点的集合为L2, 试用集合的运算表示l1、 l2的位置关系(1) 直线l1 、l2相交于一点P可以表示为:
L1 ∩ L2 = P(2)直线l1 、l2平行可以表示为:
L1 ∩ L2 = ?(3)直线l1 、l2重合可以表示为:
L1 ∩ L2 = L1 =L2问题:下列关系式成立吗?
(1) A∩A=A (2) A∩?=A3. 交集的性质 (1) A∩A=A (2) A∩?=?
(3) A∩B=B∩A (4)
(5)若x∈A∩B, 则x∈A且x∈B
(6) A∩B=A三、补集 在研究问题时,我们经常需要研究对象的范围,在不同范围研究同一问题,可能有不同的结果 问题: 在下面范围内解方程(x-2)(x2-3)=0
(1) 有理数范围 (2)实数范围 1. 全集:如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U2. 补集:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作CUA3. 补集的表示:
自然语言:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集
符号语言: CUA ={x | x∈U且x A}
图形语言:例5. 设U={x|x是小于9的正整数} ,
A={1,2,3} B={3,4,5,6} ,求CUA,CUB解:∵ U={1,2,3,4,5,6,7,8}
∴ CUA ={4,5,6,7,8}
CUB ={1,2,7,8} 例6. 设全集U={x|x是三角形} ,
A={x|x是锐角三角形} B={x|x是钝角三角形} , 求A∩B,CU(A∪B)解: A∩B=?
∵A∪B ={x|x是锐角三角形或钝角三角形}
∴CU(A∪B) ={x|x是直角三角形} 4.补集的性质
(1) ( CUA )∪A = U
(2) ( CUA )∩A = ?作业书P12: A组 6,7,8,9,10题
B组 1,2,3,4题
(1)A={1,3,5} B={2,4,6} C={1,2,3,4,5,6}
(2)A={x|x是有理数} B= {x|x是无理数}
C= {x|x是实数} 思考:实数有加法运算,类比实数的加法运算,集合是否也可以“相加”呢?1. 并集:由所有属于集合A或属于集合B的元素组成的集合,称为集合A与B的并集记作:A∪B 读作:“A并B”2. 并集的表示:
自然语言:由所有属于集合A或属于集合B的元素组成的集合,成为集合A与B的并集
符号语言: A∪B ={x | x∈A或x∈B}
图形语言:例1. 设A={4,5,6,8} , B={3,5,7,8}, 求A∪B 解:A∪B ={3,4,5,6,7,8} 注:求两个集合的并集时,它们的公共元素在并集中只能出现一次例2. 设集合A={x|-1
(3) A∪B=B∪A (4)
(5)若x∈A∪B, 则x∈A或x∈B
(6) A∪B=B二、交集 考察下列各个集合,你能说出集合C与集合A、B之间的关系吗?
(1)A={2,4,6,8,10} B={3,5,8,12} C={8}
(2)A={x|x是166中学的女同学}
B= {x|x是166中学高一年级同学}
C= {x|x是166中学高一年级女同学} 可以发现:集合C是由那些既属于集合A又属于集合B的所有元素组成的1. 交集:由属于集合A且属于集合B的所有元素组成的集合,成为集合A与B的交集记作:A∩B 读作:“A交B”2. 交集的表示:
自然语言:由属于集合A且属于集合B的所有元素组成的集合,成为集合A与B的交集
符号语言: A∩B={x | x∈A且x∈B}
图形语言:例3. 166中学开运动会,设
A={x|x是166中高一年级参加百米赛跑的同学},
B={x|x是166中高一年级参加跳高比赛的同学},
求A∩B 解:A∩B ={x|x是166中高一年级既参加百米赛跑又参加跳高比赛的同学}解:平面内直线l1 、l2可能有三种位置关系:即相交于一点,平行或重合例4. 设平面内直线l1 上点的集合为L1 ,直线l2上点的集合为L2, 试用集合的运算表示l1、 l2的位置关系(1) 直线l1 、l2相交于一点P可以表示为:
L1 ∩ L2 = P(2)直线l1 、l2平行可以表示为:
L1 ∩ L2 = ?(3)直线l1 、l2重合可以表示为:
L1 ∩ L2 = L1 =L2问题:下列关系式成立吗?
(1) A∩A=A (2) A∩?=A3. 交集的性质 (1) A∩A=A (2) A∩?=?
(3) A∩B=B∩A (4)
(5)若x∈A∩B, 则x∈A且x∈B
(6) A∩B=A三、补集 在研究问题时,我们经常需要研究对象的范围,在不同范围研究同一问题,可能有不同的结果 问题: 在下面范围内解方程(x-2)(x2-3)=0
(1) 有理数范围 (2)实数范围 1. 全集:如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U2. 补集:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作CUA3. 补集的表示:
自然语言:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集
符号语言: CUA ={x | x∈U且x A}
图形语言:例5. 设U={x|x是小于9的正整数} ,
A={1,2,3} B={3,4,5,6} ,求CUA,CUB解:∵ U={1,2,3,4,5,6,7,8}
∴ CUA ={4,5,6,7,8}
CUB ={1,2,7,8} 例6. 设全集U={x|x是三角形} ,
A={x|x是锐角三角形} B={x|x是钝角三角形} , 求A∩B,CU(A∪B)解: A∩B=?
∵A∪B ={x|x是锐角三角形或钝角三角形}
∴CU(A∪B) ={x|x是直角三角形} 4.补集的性质
(1) ( CUA )∪A = U
(2) ( CUA )∩A = ?作业书P12: A组 6,7,8,9,10题
B组 1,2,3,4题
