9.2.3总体集中趋势的估计课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册(共26张PPT)
文档属性
| 名称 | 9.2.3总体集中趋势的估计课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 17:36:46 | ||
图片预览






文档简介
(共26张PPT)
9.2.3 总体集中趋势的估计
众数、中位数、平均数
2、中位数:将一组数据按从大到小依次排列,把处在中间位置上的一个数据(或中间两个数据的平均数)叫做这组数据的中位数;
1、众数:在一组数据中,出现的次数最多的数据叫做这组数据的众数;
二:概念再现
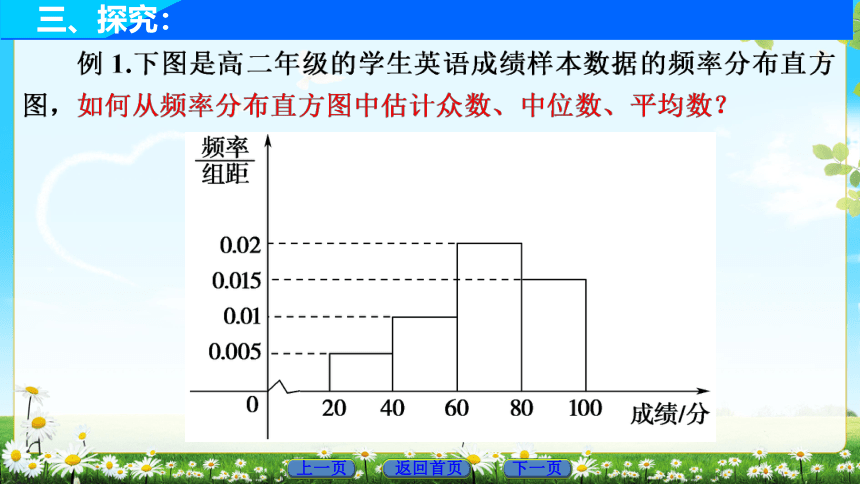
三、探究:
思考一:你认为众数应该在哪个小矩形内?
众数:
70
取最高矩形中点的横坐标作为众数
由频率分布直方图求众数:
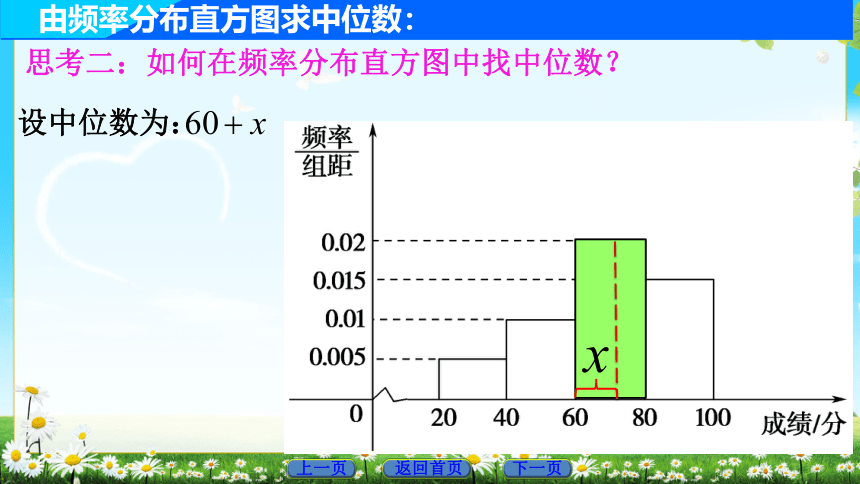
由频率分布直方图求中位数:
思考二:如何在频率分布直方图中找中位数?
设中位数为:
四、例题
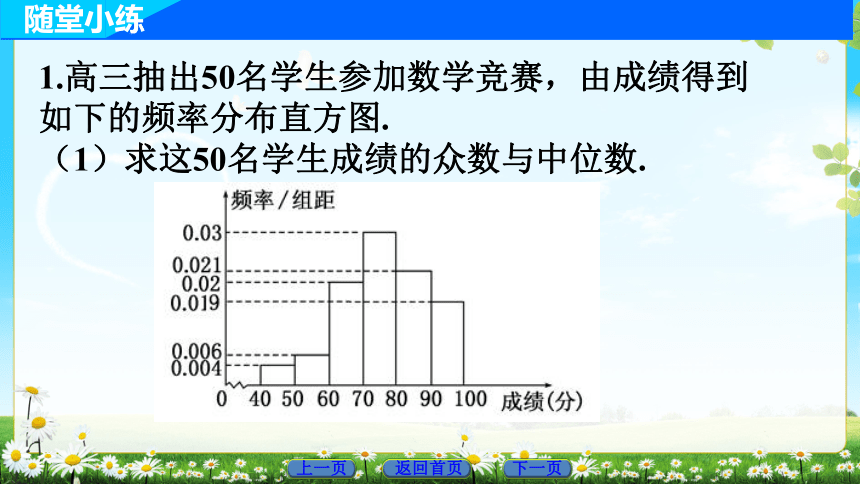
随堂小练
1.高三抽出50名学生参加数学竞赛,由成绩得到如下的频率分布直方图.
(1)求这50名学生成绩的众数与中位数.
本次100名学生周测的成绩如图,假设每组分数用该组的中间值来估计, 如何求本次周测的平均数
成绩分组 频数 频率
[40,60) 20 0.2
[60,80) 50 0.5
[80,100] 30 0.3
合计 100 1.00
平均数=每组组中值×频率之和
如何在频率分布直方图估计平均数?
由频率分布直方图求平均数:
思考三:如何在频率分布直方图估计平均数?
平均数 = 每个小矩形的面积乘以小矩形底边中点的横坐标之和
四、例题
(2)求高一参赛学生的平均成绩.
五、练习
六、小结
1.众数:最高矩形的中点的横坐标;
2.中位数:左右两侧直方图的面积相等;
3.平均数:每个小矩形底边横坐标的中点乘以小矩形的面积的乘积之和.
频率=0.5处
二、通过频率分布直方图求众数、中位数、平均数
思考4:在下图的三种分布形态中,平均数和中位数的大小存在什么关系?
平均数≈中位数
平均数大于中位数
平均数小于中位数
单峰
平均数总是在“长尾巴”那边。
右边“拖尾”
左边“拖尾”
对称
(2022·全国·高一专题练均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关,在下图两种分布形态中,分别对应平均数和中位数之一,则可能的对应关系是( )A. a为中位数,b为平均数,c为平均数,d为中位数B. a为平均数,b为中位数,c为平均数,d为中位数C. a为中位数,b为平均数,c为中位数,d为平均数D. a为平均数,b为中位数,c为中位数,d为平均数
A
四.【练】
当堂训练一
某校从参加高一年级期末考试的学生中抽出60名,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图中的信息,回答下列问题:
例3
(1)估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数);
步步高P114
众数是频率分布直方图中最高小矩
形底边中点的横坐标,所以众数为
m=75.0.
前3个小矩形面积和为0.01×10
+0.015×10+0.015×10=0.4<0.5,
前4个小矩形面积和为0.4+0.03×10=0.7>0.5,
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
依题意,60及60以上的分数在第三、
四、五、六组,频率和为(0.015+0.03
+0.025+0.005)×10=0.75,
所以估计这次考试的物理成绩的及格率
是75%.
利用组中值估算抽样学生的平均分为45×f1+55×f2+65×f3+75×f4+85×f5+95×f6=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
所以估计这次考试的物理成绩的平均分是71分.
我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.估计居民月均用水量的中位数.
跟踪训练3
由(0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.
因为前5组的频率之和为(0.08+0.16+0.30+0.42+0.50)×0.5=0.73>0.5,
而前4组的频率之和为(0.08+0.16+0.30
+0.42)×0.5=0.48<0.5.
设中位数为x吨,
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
思考1:从上述思考题和例题中,你能总结出平均数、中位数、众数各自的特点吗?
平均数 中位数 众数
在频率分布直方图中的含义 每个小矩形面积乘以小矩形底边中点的横坐标之和 把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标 最高矩形的中点的横坐标
特点 与每一个数据有关,任何一个数的改变都会引起它的改变 只利用了样本数据中间位置的一个或两个值,并未利用其他数据 只利用了出现次数最多的那一个值的信息
对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;
对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数。
思考2:根据平均数、中位数、众数各自的特点,我们应如何选择适合的统计量来表示数据的集中趋势?
思考3:你能总结用样本的众数、中位数和平均数来估计总体的数字特征各自的优缺点吗?
受极端数据的影响较大.
代表了样本数据更多的信息.
只能表达样本数据中的少量信息.
容易计算,不受少数几个极端值的影响.
平均数
众数和
中位数
缺点
优点
谢谢大家!
9.2.3 总体集中趋势的估计
众数、中位数、平均数
2、中位数:将一组数据按从大到小依次排列,把处在中间位置上的一个数据(或中间两个数据的平均数)叫做这组数据的中位数;
1、众数:在一组数据中,出现的次数最多的数据叫做这组数据的众数;
二:概念再现
三、探究:
思考一:你认为众数应该在哪个小矩形内?
众数:
70
取最高矩形中点的横坐标作为众数
由频率分布直方图求众数:
由频率分布直方图求中位数:
思考二:如何在频率分布直方图中找中位数?
设中位数为:
四、例题
随堂小练
1.高三抽出50名学生参加数学竞赛,由成绩得到如下的频率分布直方图.
(1)求这50名学生成绩的众数与中位数.
本次100名学生周测的成绩如图,假设每组分数用该组的中间值来估计, 如何求本次周测的平均数
成绩分组 频数 频率
[40,60) 20 0.2
[60,80) 50 0.5
[80,100] 30 0.3
合计 100 1.00
平均数=每组组中值×频率之和
如何在频率分布直方图估计平均数?
由频率分布直方图求平均数:
思考三:如何在频率分布直方图估计平均数?
平均数 = 每个小矩形的面积乘以小矩形底边中点的横坐标之和
四、例题
(2)求高一参赛学生的平均成绩.
五、练习
六、小结
1.众数:最高矩形的中点的横坐标;
2.中位数:左右两侧直方图的面积相等;
3.平均数:每个小矩形底边横坐标的中点乘以小矩形的面积的乘积之和.
频率=0.5处
二、通过频率分布直方图求众数、中位数、平均数
思考4:在下图的三种分布形态中,平均数和中位数的大小存在什么关系?
平均数≈中位数
平均数大于中位数
平均数小于中位数
单峰
平均数总是在“长尾巴”那边。
右边“拖尾”
左边“拖尾”
对称
(2022·全国·高一专题练均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关,在下图两种分布形态中,分别对应平均数和中位数之一,则可能的对应关系是( )A. a为中位数,b为平均数,c为平均数,d为中位数B. a为平均数,b为中位数,c为平均数,d为中位数C. a为中位数,b为平均数,c为中位数,d为平均数D. a为平均数,b为中位数,c为中位数,d为平均数
A
四.【练】
当堂训练一
某校从参加高一年级期末考试的学生中抽出60名,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图中的信息,回答下列问题:
例3
(1)估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数);
步步高P114
众数是频率分布直方图中最高小矩
形底边中点的横坐标,所以众数为
m=75.0.
前3个小矩形面积和为0.01×10
+0.015×10+0.015×10=0.4<0.5,
前4个小矩形面积和为0.4+0.03×10=0.7>0.5,
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
依题意,60及60以上的分数在第三、
四、五、六组,频率和为(0.015+0.03
+0.025+0.005)×10=0.75,
所以估计这次考试的物理成绩的及格率
是75%.
利用组中值估算抽样学生的平均分为45×f1+55×f2+65×f3+75×f4+85×f5+95×f6=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
所以估计这次考试的物理成绩的平均分是71分.
我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查.通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.估计居民月均用水量的中位数.
跟踪训练3
由(0.08+0.16+a+0.42+0.50+a+0.12+0.08+0.04)×0.5=1,解得a=0.30.
因为前5组的频率之和为(0.08+0.16+0.30+0.42+0.50)×0.5=0.73>0.5,
而前4组的频率之和为(0.08+0.16+0.30
+0.42)×0.5=0.48<0.5.
设中位数为x吨,
由0.50×(x-2)=0.5-0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
思考1:从上述思考题和例题中,你能总结出平均数、中位数、众数各自的特点吗?
平均数 中位数 众数
在频率分布直方图中的含义 每个小矩形面积乘以小矩形底边中点的横坐标之和 把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标 最高矩形的中点的横坐标
特点 与每一个数据有关,任何一个数的改变都会引起它的改变 只利用了样本数据中间位置的一个或两个值,并未利用其他数据 只利用了出现次数最多的那一个值的信息
对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;
对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数。
思考2:根据平均数、中位数、众数各自的特点,我们应如何选择适合的统计量来表示数据的集中趋势?
思考3:你能总结用样本的众数、中位数和平均数来估计总体的数字特征各自的优缺点吗?
受极端数据的影响较大.
代表了样本数据更多的信息.
只能表达样本数据中的少量信息.
容易计算,不受少数几个极端值的影响.
平均数
众数和
中位数
缺点
优点
谢谢大家!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
