等式性质[上学期]

课件25张PPT。数学是科学的皇后
——高斯四中 王敏敏一元一次方程及其解法想一想: 1.什么叫方程？ 含有未知数的等式叫方程。
？ 等式的性质（一） 2. 方程的解与解方程
使方程中等号左右两边相等的 的值，就是方程的解。
解方程就是求方程的解的过程。未知数 回眸一看猜猜你的年龄 把你的年龄乘以2减去5的得数告诉我，我就能猜出你的年龄。 设你的年龄为X，得：
2X-5=某个数小明今年12岁，他爸爸36岁，问在过几年，他爸爸年龄是他年龄的2倍？ 设再过X年他爸爸年龄是他年龄的2倍，得：
36+X=2（12+X）这种方程都：只含有一个未知数（元），并且未知数的次数都是1，这样的方程叫一元一次方程 等式的性质（一）　　　　新知探究等式的性质？　　　　　　　看一看:1+2　 =　3　　
a+b　=　b+a
　S　 =　ab
4+x　 =　7
你发现： 这4个式子的共同点是
它们表示了 关系。含有“=”号相等 像这种用等号“=”来表示相等关系的式子，叫做等式。一般的等式我们可以用 表示。
在等式中，等号左、右两边的式子，分别叫做这个等式的左边、右边。a=b 等式的性质（一）下列式子是否为等式？
① ab=ba ② s=vt
③ a＞0 ④ xy+4
⑤ 2a ⑥ y=5
⑦ 4x+3y=8解：是等式的有：

不是等式的有：
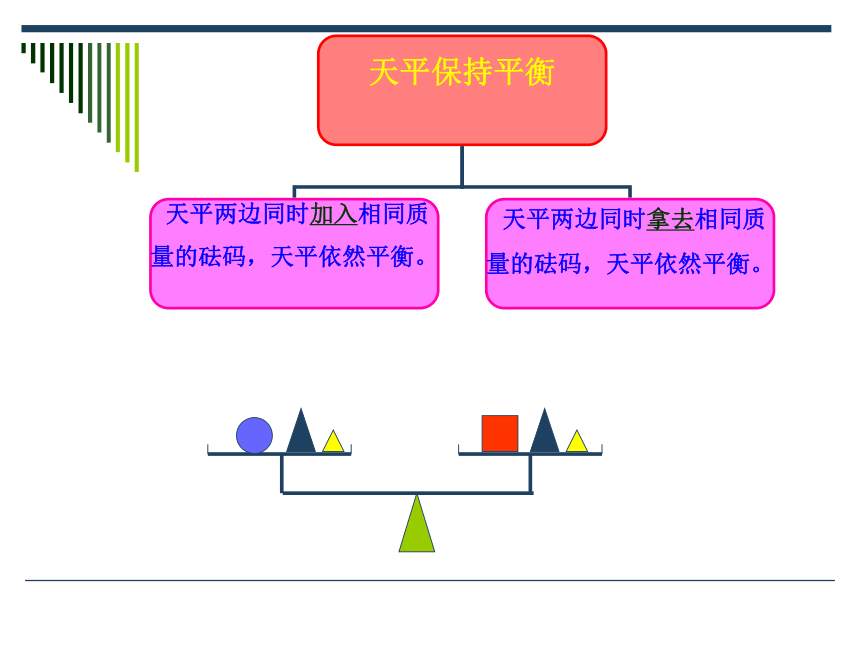
① ② ⑥ ⑦③ ④ ⑤口答：天平保持平衡
天平两边同时加入相同质
量的砝码，天平依然平衡。
天平两边同时拿去相同质
量的砝码，天平依然平衡。
天平保持平衡

天平两边同时扩大到原来相
同的倍数，天平依然平衡。

天平两边同时缩小到原来的
几分之几，天平依然平衡。
试一试：你能用式子的形式表示等式的性质吗？性质1用式子的形式可以表示为：
如果 a = b，那么 a ± c =
性质2用式子的形式可以表示为：
如果 a = b，那么 a c =
如果 a = b，且c≠0，那么 b ± c
b c
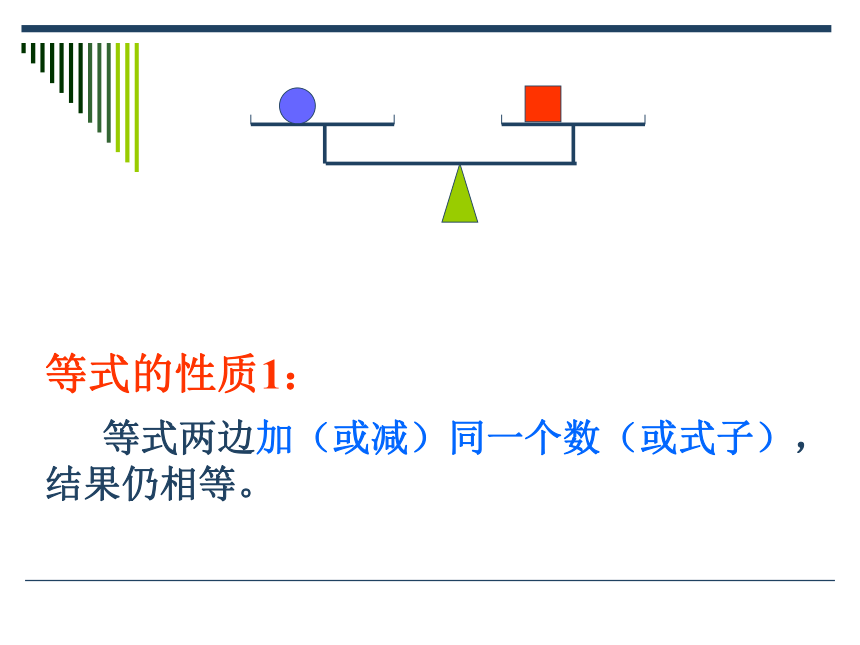
等式两边加（或减）同一个数（或式子），结果仍相等。
等式两边乘同一个数（或式子），或除以同一个非0的数（或式子）结果仍相等。已知：X=Y 字母a可取任何值（成立）（成立）（以上两题等式性质1）（成立）（成立）（成立）（3、4、5题等式性质2）（不一定成立）当a=5时等式两边都没有意义动脑筋例1.解下列方程：（1）x+7=26 （2）3=x－5解： （1）方程两边同时减7，得
x+7-7=26-7 （等式性质1）
于是 x=19
（2）方程两边同时加5，得
3+5=x-5+5 （等式性质1）
于是 8=x
习惯上，我们写为x=8.
试一试： 例2.利用等式的性质解下列方程：

（1）-5x=20 （2） 3x-5=22
解： （1）方程两边同时除以-5，得
-5x÷（-5）=20÷（-5）（等式性质2）
于是 x =-4

也可以写成试一试： 例2.利用等式的性质解下列方程：
（1）-5x=20 （2） 3x-5=22
解： （2）3x-5+5=22+5 （等式性质1）
3x=27 （等式性质2）
x=9
问一问：怎样验证你得到答案对不对呢？例2.利用等式的性质解下列方程：
（1）-5x=20 （2） 3x-5=22
解： （2）3x-5+5=22+5 （等式性质1）
3x=27 （等式性质2）
x=9
检验：将x=9 代入原方程，
左边=3×9-5=27-5=22
右边=22
左边=右边
所以x=9是原方程的解将数值分别代入方程的左边、右边，计算后，如果左边=右边，那么此数值是原方程的解，反之，不是。做一做：1.以下等式变形，正确的打“√”,错误的打“×”
由x = y，得到 x＋5 ＝ y＋5
由 2 a +1 = b+1，得到 2 a = b
③ 由 m = n，得到 a m = a n
④ 由a m = a n ，得到 m = n
√×√√ 2.下列各式的变形正确的是（ ）
A.由 ，得到 x = 2
B.由 ，得到 x = 1
C.由－2 a = －3，得到 a =
D.由 x－1 = 4，得到 x = 5Dx = 0x = 9a =等式的性质1等式的性质2等式的性质2－y+2 +2=③ 若 －x = y，根据___________，得到 x =____ 。4.利用等式的性质解下列方程并检验：
(1)x-5=6 (2)0.3x=45
(3)2- x=3 (4)5x+4=0归纳总结：2、解一元一次方程的实质就是利用
等式的性质求出未知数的值。
　　将方程化为“x=?” 的形式。1、等式的两条性质；
① 如果 a = b，那么 a ± c = b ± c
② 如果 a = b，那么 a c = b c
如果 a = b，那么 （c≠ 0） 猜一猜：如图，
是2006年四月份的日历，现用一正方形在日历中任意框出四个数 ，
请用一个等式表示a、b、c、d之间的关系：a b
c d
作业：
教材 P85 1题
交送作业：P88 1 （2）（4）
2（2）（4） 祝同学们学习进步！goodbye