山东省泰安市宁阳县(五四学制)2022-2023学年七年级下学期期末数学试题(无答案)
文档属性
| 名称 | 山东省泰安市宁阳县(五四学制)2022-2023学年七年级下学期期末数学试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 599.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 00:00:00 | ||
图片预览

文档简介
七年级数学试题
满分150分 时间120分钟
一、选择题(本题共12个小题,每小题4分,共48分)
1.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽3个、腊肉粽2个、白米粽4个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个.选到甜粽的概率是( )
A. B. C. D.
2.下列命题是假命题的是( )
A.有一个角是的等腰三角形是等边三角形
B.有两边长一角对应相等的两个三角形全等
C.平面内垂直于同一直线的两条直线平行
D.全等三角形的面积相等
3.将一把直尺和一块含和角的三角板按如图所示的位置放置,如果,那么的大小为( )
A. B. C. D.
4.若,则下列不等式不一定成立的是( )
A. B. C. D.
5.以方程组的解为坐标的点在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,在平面直角坐标系中,直线和相交于点,则不等式的解集为( )
A. B. C. D.
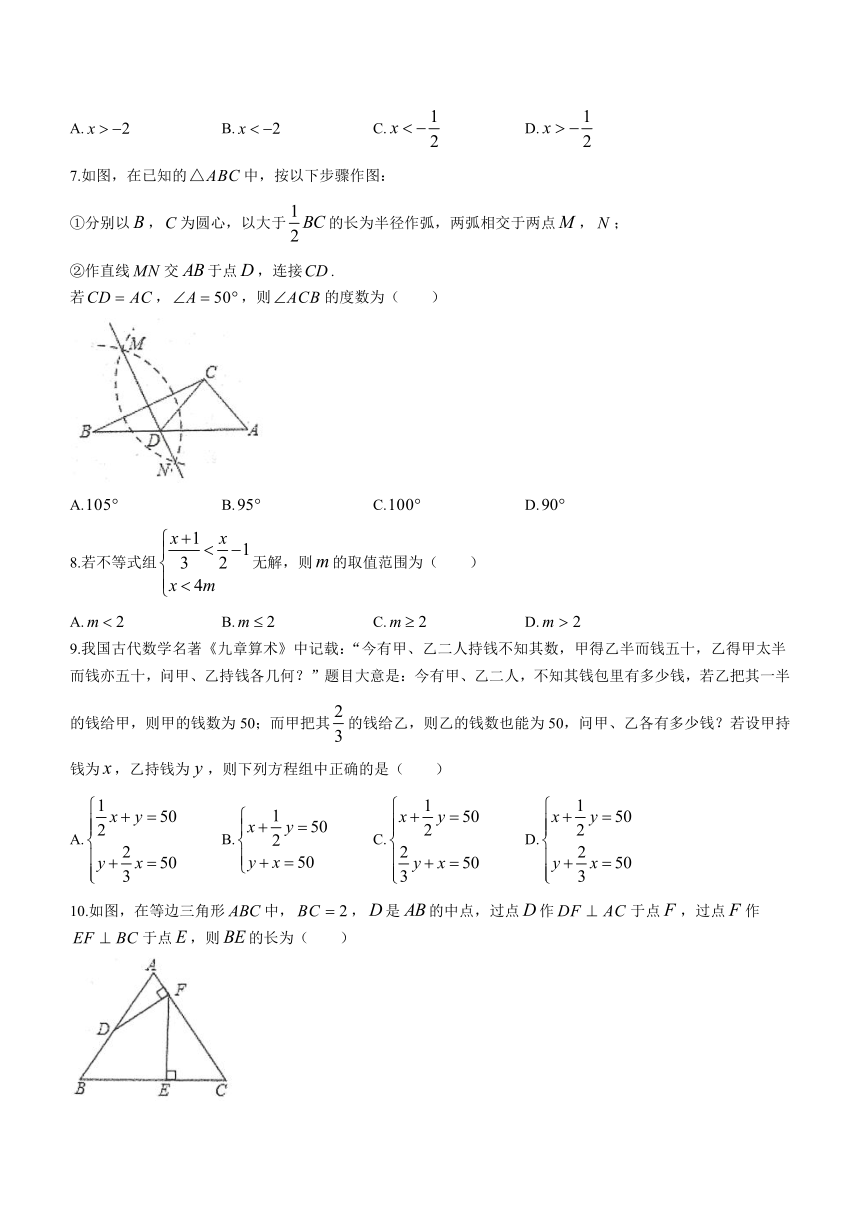
7.如图,在已知的中,按以下步骤作图:
①分别以,为圆心,以大于的长为半径作弧,两弧相交于两点,;
②作直线交于点,连接.
若,,则的度数为( )
A. B. C. D.
8.若不等式组无解,则的取值范围为( )
A. B. C. D.
9.我国古代数学名著《九章算术》中记载:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十,问甲、乙持钱各几何?”题目大意是:今有甲、乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为,乙持钱为,则下列方程组中正确的是( )
A. B. C. D.
10.如图,在等边三角形中,,是的中点,过点作于点,过点作于点,则的长为( )
A.1 B. C. D.
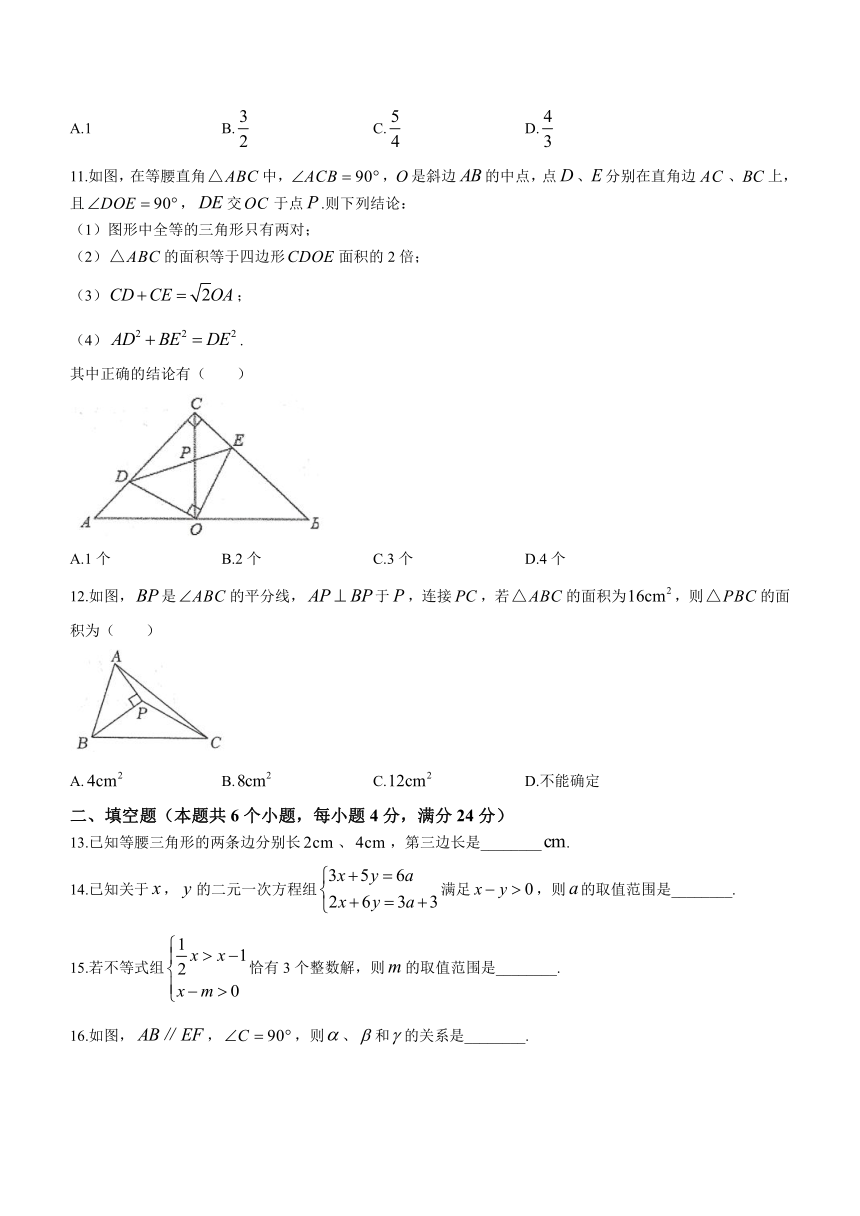
11.如图,在等腰直角中,,是斜边的中点,点、分别在直角边、上,且,交于点.则下列结论:
(1)图形中全等的三角形只有两对;
(2)的面积等于四边形面积的2倍;
(3);
(4).
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图,是的平分线,于,连接,若的面积为,则的面积为( )
A. B. C. D.不能确定
二、填空题(本题共6个小题,每小题4分,满分24分)
13.已知等腰三角形的两条边分别长、,第三边长是________.
14.已知关于,的二元一次方程组满足,则的取值范围是________.
15.若不等式组恰有3个整数解,则的取值范围是________.
16.如图,,,则、和的关系是________.
17.如图,中,,平分交于点,交的延长线于点,交于点.若,,.则的长为________.
18.将从1开始的自然数按以下规律排列,例如位于第3行、第4列的数是12,则位于第6行、第5列的数是________.
三、解答题(共7小题,共78分)
19.计算题(15分)
(1)解不等式:
(2)解方程组:
(3)解不等式组:
20.(7分)一个不透明的口袋中放着若干个红球和黑球,这两种球除颜色外没有其他任何区别,袋中的球已经搅匀,闭眼从口袋中摸出一个球,记下颜色后放回搅匀,经过大量重复试验发现摸到黑球的频率逐渐稳定在0.4附近.
(1)估计摸到红球的概率是________;
(2)如果袋中有黑球12个,求袋中有几个球;
(3)在(2)的条件下,又放入个黑球,再经过大量重复试验发现摸到黑球的频率逐渐稳定在0.7附近,求的值.
21.(9分)综合与探究:
如图,在平面直角坐标系中,一次函数的图象分别交、轴于点、,点在轴上,平分.
(1)求点、的坐标;
(2)求线段的长;
22.(11分)如图,在中,,为的中点,,分别为,上的点,且.
(1)求证:.
(2)若,,求的度数.
23.(12分)“文化衫”,无形之间会凝聚一个团队的力量,更好的体现活动的愿望和个性.为使活动更具意义,某活动举办方决定购买甲、乙两种品牌的文化衫,已知购买3件甲品牌文化衫和2件乙品牌文化衫需190元;购买5件甲品牌文化衫和1件乙品牌文化衫需235元.
(1)求甲、乙两种品牌文化衫的单价;
(2)根据需要,举办方决定购买两种品牌的文化衫共1000件,已知甲品牌文化衫的件数的不少于乙品牌文化衫件数的2倍.那么举办方至少购买甲品牌的文化衫多少件?
24.(12分)如图,线段与交于点,点为上一点,连接、、,已知,.
(1)请添加一个条件________使,并说明理由.
(2)在(1)的条件下请探究与的数量关系,并说明理由.
25.(12分)已知和都是等腰直角三角形(),.
(1)如图1:连,,求证:;
(2)若将绕点顺时针旋转,如图2,当点恰好在边上时,求证:;
满分150分 时间120分钟
一、选择题(本题共12个小题,每小题4分,共48分)
1.端午佳节,小明妈妈准备了豆沙粽2个、红枣粽3个、腊肉粽2个、白米粽4个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个.选到甜粽的概率是( )
A. B. C. D.
2.下列命题是假命题的是( )
A.有一个角是的等腰三角形是等边三角形
B.有两边长一角对应相等的两个三角形全等
C.平面内垂直于同一直线的两条直线平行
D.全等三角形的面积相等
3.将一把直尺和一块含和角的三角板按如图所示的位置放置,如果,那么的大小为( )
A. B. C. D.
4.若,则下列不等式不一定成立的是( )
A. B. C. D.
5.以方程组的解为坐标的点在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,在平面直角坐标系中,直线和相交于点,则不等式的解集为( )
A. B. C. D.
7.如图,在已知的中,按以下步骤作图:
①分别以,为圆心,以大于的长为半径作弧,两弧相交于两点,;
②作直线交于点,连接.
若,,则的度数为( )
A. B. C. D.
8.若不等式组无解,则的取值范围为( )
A. B. C. D.
9.我国古代数学名著《九章算术》中记载:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十,问甲、乙持钱各几何?”题目大意是:今有甲、乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为,乙持钱为,则下列方程组中正确的是( )
A. B. C. D.
10.如图,在等边三角形中,,是的中点,过点作于点,过点作于点,则的长为( )
A.1 B. C. D.
11.如图,在等腰直角中,,是斜边的中点,点、分别在直角边、上,且,交于点.则下列结论:
(1)图形中全等的三角形只有两对;
(2)的面积等于四边形面积的2倍;
(3);
(4).
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图,是的平分线,于,连接,若的面积为,则的面积为( )
A. B. C. D.不能确定
二、填空题(本题共6个小题,每小题4分,满分24分)
13.已知等腰三角形的两条边分别长、,第三边长是________.
14.已知关于,的二元一次方程组满足,则的取值范围是________.
15.若不等式组恰有3个整数解,则的取值范围是________.
16.如图,,,则、和的关系是________.
17.如图,中,,平分交于点,交的延长线于点,交于点.若,,.则的长为________.
18.将从1开始的自然数按以下规律排列,例如位于第3行、第4列的数是12,则位于第6行、第5列的数是________.
三、解答题(共7小题,共78分)
19.计算题(15分)
(1)解不等式:
(2)解方程组:
(3)解不等式组:
20.(7分)一个不透明的口袋中放着若干个红球和黑球,这两种球除颜色外没有其他任何区别,袋中的球已经搅匀,闭眼从口袋中摸出一个球,记下颜色后放回搅匀,经过大量重复试验发现摸到黑球的频率逐渐稳定在0.4附近.
(1)估计摸到红球的概率是________;
(2)如果袋中有黑球12个,求袋中有几个球;
(3)在(2)的条件下,又放入个黑球,再经过大量重复试验发现摸到黑球的频率逐渐稳定在0.7附近,求的值.
21.(9分)综合与探究:
如图,在平面直角坐标系中,一次函数的图象分别交、轴于点、,点在轴上,平分.
(1)求点、的坐标;
(2)求线段的长;
22.(11分)如图,在中,,为的中点,,分别为,上的点,且.
(1)求证:.
(2)若,,求的度数.
23.(12分)“文化衫”,无形之间会凝聚一个团队的力量,更好的体现活动的愿望和个性.为使活动更具意义,某活动举办方决定购买甲、乙两种品牌的文化衫,已知购买3件甲品牌文化衫和2件乙品牌文化衫需190元;购买5件甲品牌文化衫和1件乙品牌文化衫需235元.
(1)求甲、乙两种品牌文化衫的单价;
(2)根据需要,举办方决定购买两种品牌的文化衫共1000件,已知甲品牌文化衫的件数的不少于乙品牌文化衫件数的2倍.那么举办方至少购买甲品牌的文化衫多少件?
24.(12分)如图,线段与交于点,点为上一点,连接、、,已知,.
(1)请添加一个条件________使,并说明理由.
(2)在(1)的条件下请探究与的数量关系,并说明理由.
25.(12分)已知和都是等腰直角三角形(),.
(1)如图1:连,,求证:;
(2)若将绕点顺时针旋转,如图2,当点恰好在边上时,求证:;
同课章节目录
