数学人教A版(2019)选择性必修第二册5.2.1基本初等函数的导数 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.2.1基本初等函数的导数 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 19:15:25 | ||
图片预览





文档简介
(共15张PPT)
5.2.1基本初等函数的导数
教学目标
一.能根据导数的定义推导出常用函数的导数
二.掌握基本初等函数导数公式,能利用公式进行计算
重、难点
一.基本初等函数的导数公式
二.基本初等函数导数公式的应用
导函数的概念
复习回顾
根据导数的定义,求函数y=f (x)的导数,就是求出当Δx →0时, 无限趋近的那个定值.
探究新知
1.函数 y=f (x)=c 的导数
x
y
O
y=c
∵
探究新知
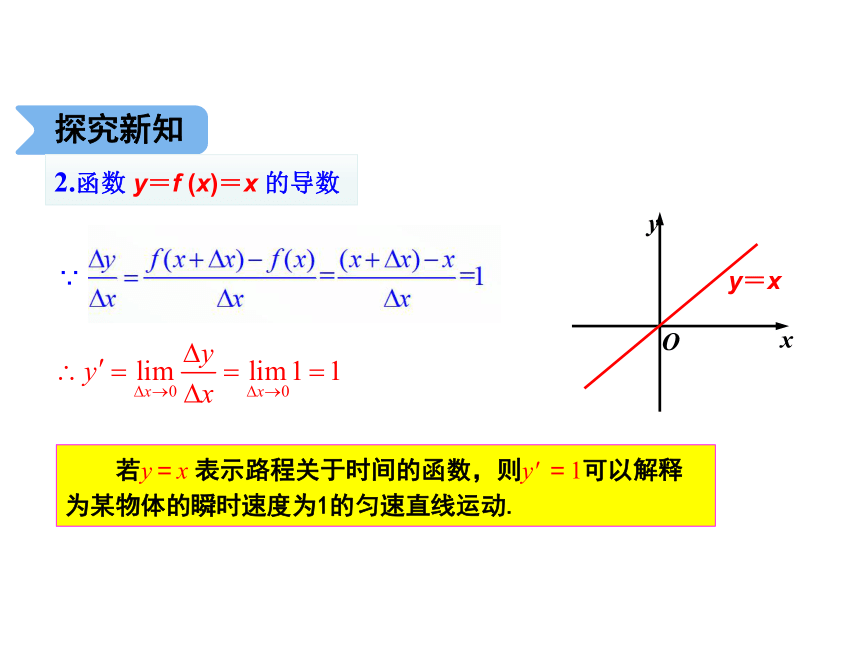
2.函数 y=f (x)=x 的导数
x
y
O
y=x
若y=x 表示路程关于时间的函数,则y′ =1可以解释为某物体的瞬时速度为1的匀速直线运动.
∵
探究新知
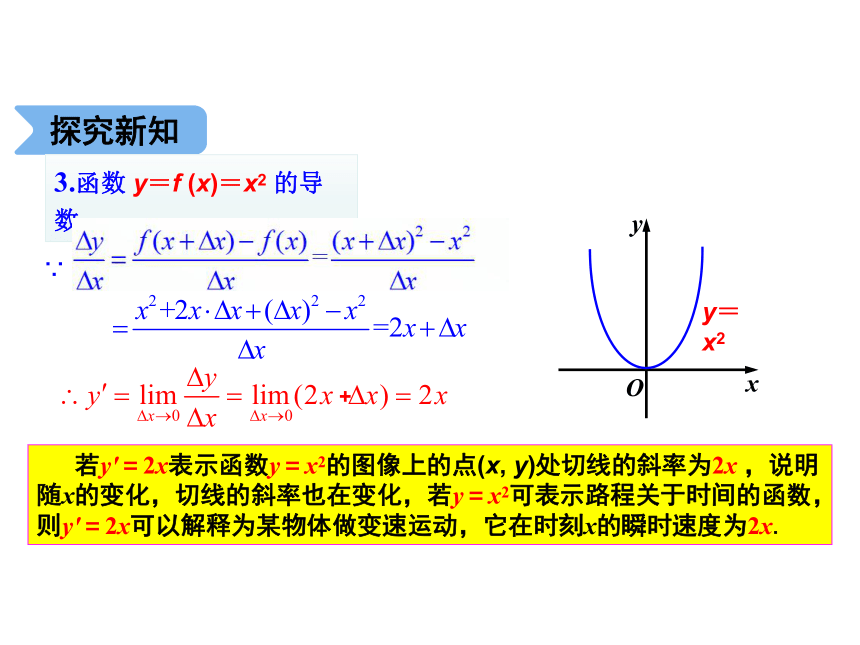
3.函数 y=f (x)=x2 的导数
x
y
O
y=x2
若y′=2x表示函数y=x2的图像上的点(x, y)处切线的斜率为2x ,说明随x的变化,切线的斜率也在变化,若y=x2可表示路程关于时间的函数,则y′=2x可以解释为某物体做变速运动,它在时刻x的瞬时速度为2x.
∵
+
探究新知
4.函数 y=f (x)=x3 的导数
x
y
O
y=x3
若y′=3x2表示函数y=x3的图像上的点(x, y)处切线的斜率为3x2,这说明随x的变化,切线的斜率也在变化,且恒为非负数.
∵
探究新知
5.函数 y=f (x)= 的导数
x
1
—
∵
探究新知
6.函数 y=f (x)= 的导数
∵
基本初等函数的导数公式
(a∈R,且a≠0);
解:
例1 求下列函数的导数
典例分析
典例分析
1.求下列函数的导数:
课堂练习
课堂小结
基本初等函数的导数公式
(a∈R,且a≠0);
课后作业
课本75页练习第3、4题
5.2.1基本初等函数的导数
教学目标
一.能根据导数的定义推导出常用函数的导数
二.掌握基本初等函数导数公式,能利用公式进行计算
重、难点
一.基本初等函数的导数公式
二.基本初等函数导数公式的应用
导函数的概念
复习回顾
根据导数的定义,求函数y=f (x)的导数,就是求出当Δx →0时, 无限趋近的那个定值.
探究新知
1.函数 y=f (x)=c 的导数
x
y
O
y=c
∵
探究新知
2.函数 y=f (x)=x 的导数
x
y
O
y=x
若y=x 表示路程关于时间的函数,则y′ =1可以解释为某物体的瞬时速度为1的匀速直线运动.
∵
探究新知
3.函数 y=f (x)=x2 的导数
x
y
O
y=x2
若y′=2x表示函数y=x2的图像上的点(x, y)处切线的斜率为2x ,说明随x的变化,切线的斜率也在变化,若y=x2可表示路程关于时间的函数,则y′=2x可以解释为某物体做变速运动,它在时刻x的瞬时速度为2x.
∵
+
探究新知
4.函数 y=f (x)=x3 的导数
x
y
O
y=x3
若y′=3x2表示函数y=x3的图像上的点(x, y)处切线的斜率为3x2,这说明随x的变化,切线的斜率也在变化,且恒为非负数.
∵
探究新知
5.函数 y=f (x)= 的导数
x
1
—
∵
探究新知
6.函数 y=f (x)= 的导数
∵
基本初等函数的导数公式
(a∈R,且a≠0);
解:
例1 求下列函数的导数
典例分析
典例分析
1.求下列函数的导数:
课堂练习
课堂小结
基本初等函数的导数公式
(a∈R,且a≠0);
课后作业
课本75页练习第3、4题
