数学八年级上青岛版2.6等腰三角形课件
文档属性
| 名称 | 数学八年级上青岛版2.6等腰三角形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 722.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-17 10:44:37 | ||
图片预览

文档简介
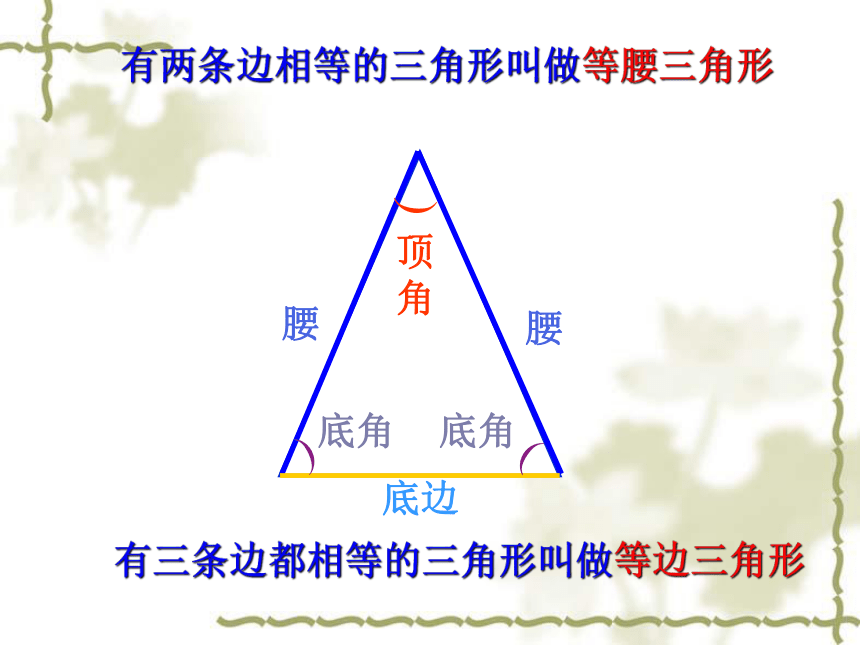
课件17张PPT。§2.6等腰三角形(1)有两条边相等的三角形叫做等腰三角形顶角底边(有三条边都相等的三角形叫做等边三角形实验与探究(1)已知等腰三角形的底边与一腰,你能用尺规作出
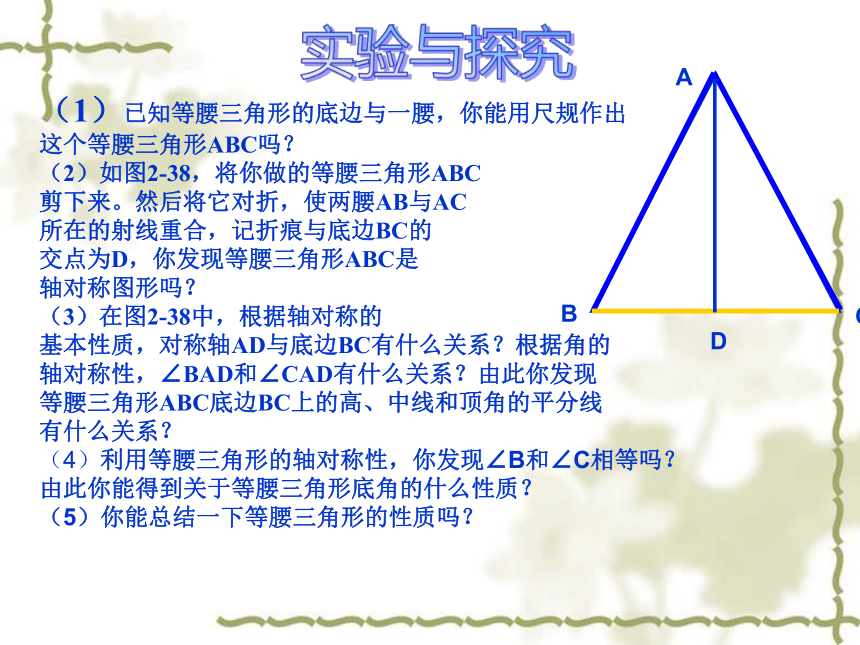
这个等腰三角形ABC吗?
(2)如图2-38,将你做的等腰三角形ABC
剪下来。然后将它对折,使两腰AB与AC
所在的射线重合,记折痕与底边BC的
交点为D,你发现等腰三角形ABC是
轴对称图形吗?
(3)在图2-38中,根据轴对称的
基本性质,对称轴AD与底边BC有什么关系?根据角的
轴对称性,∠BAD和∠CAD有什么关系?由此你发现
等腰三角形ABC底边BC上的高、中线和顶角的平分线
有什么关系?
(4)利用等腰三角形的轴对称性,你发现∠B和∠C相等吗?
由此你能得到关于等腰三角形底角的什么性质?
(5)你能总结一下等腰三角形的性质吗?
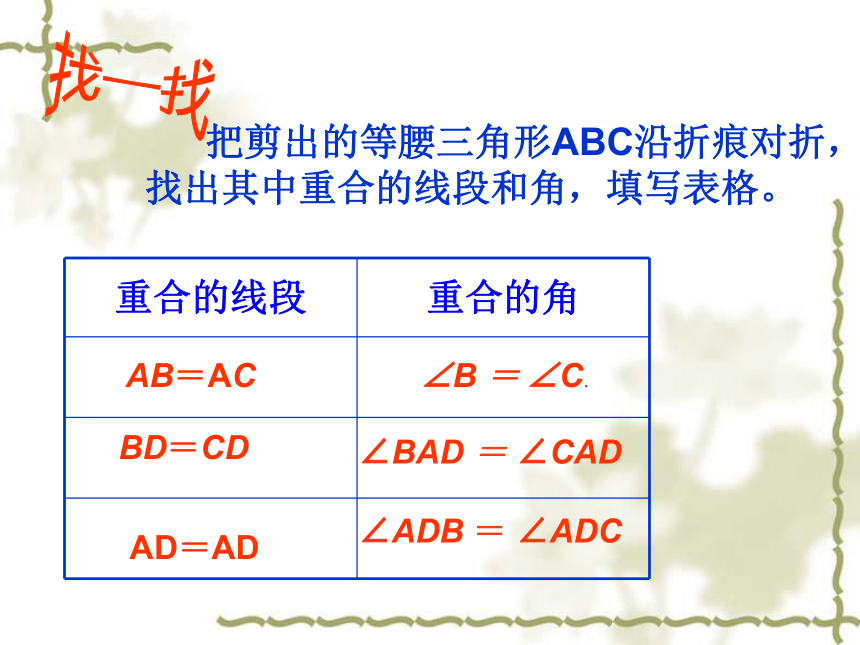
把剪出的等腰三角形ABC沿折痕对折, 找出其中重合的线段和角,填写表格。找一找 AB=AC BD=CD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC AD=AD猜想与论证等腰三角形的两个底角相等。
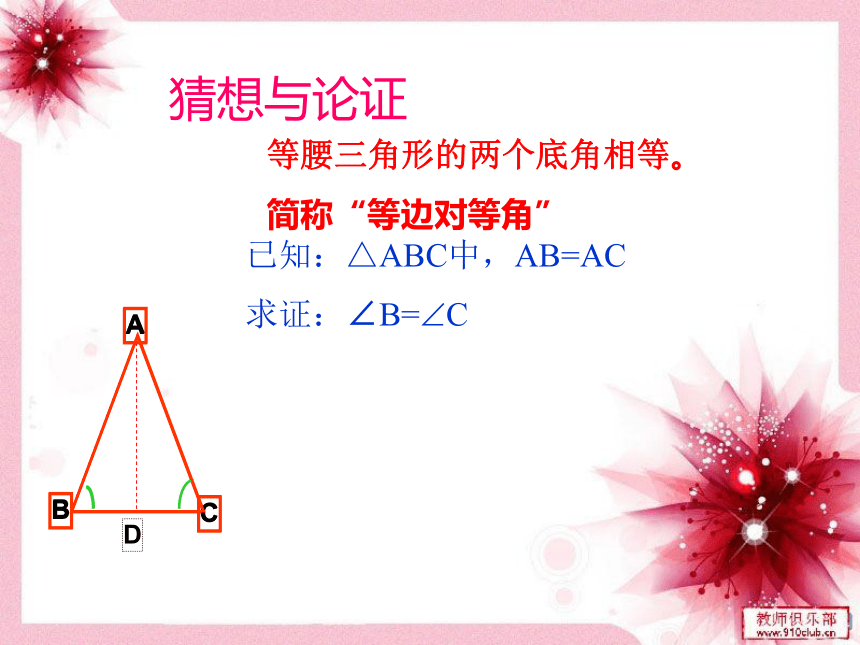
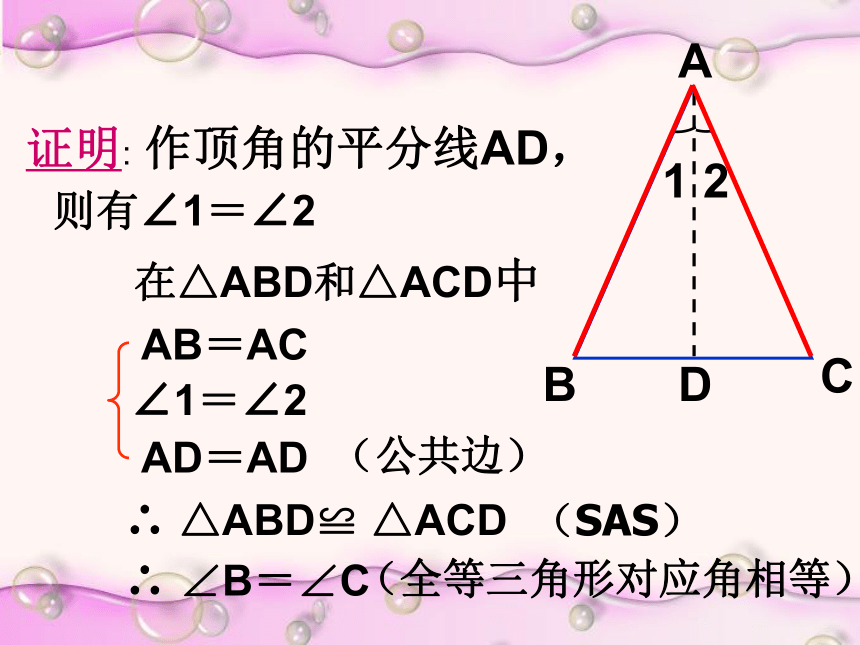
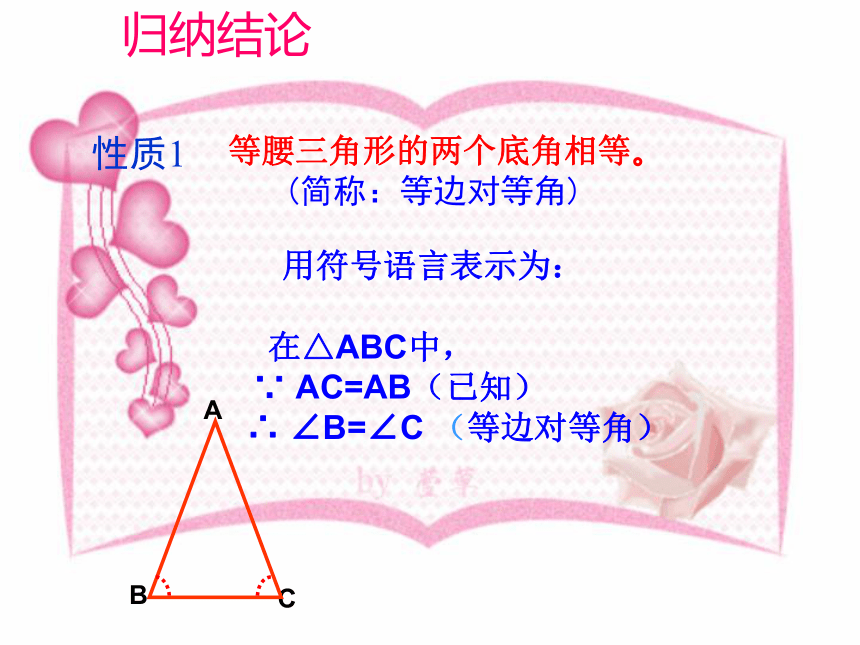
简称“等边对等角”已知:△ABC中,AB=AC求证:∠B=?C则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 归纳结论等腰三角形的两个底角相等。性质1(简称:等边对等角)用符号语言表示为: 在△ABC中,
∵ AC=AB(已知)
∴ ∠B=∠C (等边对等角)想一想: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
A B D C AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC= 90°1 2在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ ,____= 。
2、∵AD是角平分线,
∴ ⊥ , = 。
3、∵AD是中线,
∴ ⊥ , ∠ = ∠ 。112BDDCADBC12ADBC BD DC用符号语言表示为:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。
也称“三线合一”。性质2等腰三角形的性质等腰三角形是轴对称图形。等腰三角形的对称轴是底边的垂直平分线。等腰三角形的顶角平分线、底边上的高、底边上的中线重合(也称三线合一)。等腰三角形的两个底角相等。
(简称“等边对等角”)例2达标检测1、下列图形中,不是轴对称图形的是( )
A. 等腰三角形 B. 线段 C. 钝角 D. 直角三角形
2、等腰三角形的底角是顶角的2倍,则底角度数为( )
A. 36° B. 32° C. 64° D. 72°
3、等腰三角形的对称轴是___________ 。
4、如果等腰三角形的一个底角是50o,它的顶角是多少度?
5、顶角是直角的等腰三角形叫做等腰直角三角形。等腰直角三角形的两个底角分别是多少度?
6、如图,在以点A为圆心的两个同心圆中,
一条直线与这两个同心圆分别相交于B,E,D,C
四个点。请找出图中相等的线段和相等的角,
并说明理由挑战自我 如图2-42,在Rt△ABC中,∠C=90o,把直角边BC沿过点B的某条直线折叠,使点C落到斜边AB上的一点D处,当∠A为多少度时,点D恰为AB的中点?说明你的结论。等腰三角形1、等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。2、等腰三角形的顶角平分线,底边上的高、底边上的中线重合(三线合一)课堂小结3、等腰三角形的两个底角相等。课堂练习练习一
1、下列图形中,不是轴对称图形的是( )
A. 等腰三角形 B. 线段
C. 钝角 D. 直角三角形
2、等腰三角形的底角是顶角的2倍,则底角度数为( )
A. 36° B. 32° C. 64° D. 72°
3、等腰三角形的对称轴是___________ 。DD底边的垂直平分线4、分别找出如图所示中各个图形的对称轴。练习二、
1、等腰三角形底边上的高与一腰所成的角等于( )
A. 顶角 B. 顶角的一半
C. 顶角的两倍 D. 底角的一半
2、等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是( )
A. 9cm B. 12cm
C. 9cm或12cm D. 在9cm与12cm之间课堂练习3、如图,等腰△ABC中,AD⊥BC于D,已知DC=2cm,AB=3cm,则△ABC的周长为___________。4、已知:等腰三角形的一个角是80°,则它的另外两个角是 。ABCDBB10cm50°、50°或80°、20°作业习题1、5 惜时如金
这个等腰三角形ABC吗?
(2)如图2-38,将你做的等腰三角形ABC
剪下来。然后将它对折,使两腰AB与AC
所在的射线重合,记折痕与底边BC的
交点为D,你发现等腰三角形ABC是
轴对称图形吗?
(3)在图2-38中,根据轴对称的
基本性质,对称轴AD与底边BC有什么关系?根据角的
轴对称性,∠BAD和∠CAD有什么关系?由此你发现
等腰三角形ABC底边BC上的高、中线和顶角的平分线
有什么关系?
(4)利用等腰三角形的轴对称性,你发现∠B和∠C相等吗?
由此你能得到关于等腰三角形底角的什么性质?
(5)你能总结一下等腰三角形的性质吗?
把剪出的等腰三角形ABC沿折痕对折, 找出其中重合的线段和角,填写表格。找一找 AB=AC BD=CD ∠B = ∠C.∠BAD = ∠CAD∠ADB = ∠ADC AD=AD猜想与论证等腰三角形的两个底角相等。
简称“等边对等角”已知:△ABC中,AB=AC求证:∠B=?C则有∠1=∠2D12在△ABD和△ACD中证明: 作顶角的平分线AD,AB=AC ∠1=∠2 AD=AD (公共边) ∴ △ABD≌ △ACD (SAS) ∴ ∠B=∠C (全等三角形对应角相等) 归纳结论等腰三角形的两个底角相等。性质1(简称:等边对等角)用符号语言表示为: 在△ABC中,
∵ AC=AB(已知)
∴ ∠B=∠C (等边对等角)想一想: 刚才的证明除了能得到∠B=∠C 你还能发现什么?
A B D C AB=AC BD=CD AD=AD ∠B = ∠C.∠BAD = ∠CAD ∠ADB =∠ADC= 90°1 2在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ ,____= 。
2、∵AD是角平分线,
∴ ⊥ , = 。
3、∵AD是中线,
∴ ⊥ , ∠ = ∠ 。112BDDCADBC12ADBC BD DC用符号语言表示为:等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。
也称“三线合一”。性质2等腰三角形的性质等腰三角形是轴对称图形。等腰三角形的对称轴是底边的垂直平分线。等腰三角形的顶角平分线、底边上的高、底边上的中线重合(也称三线合一)。等腰三角形的两个底角相等。
(简称“等边对等角”)例2达标检测1、下列图形中,不是轴对称图形的是( )
A. 等腰三角形 B. 线段 C. 钝角 D. 直角三角形
2、等腰三角形的底角是顶角的2倍,则底角度数为( )
A. 36° B. 32° C. 64° D. 72°
3、等腰三角形的对称轴是___________ 。
4、如果等腰三角形的一个底角是50o,它的顶角是多少度?
5、顶角是直角的等腰三角形叫做等腰直角三角形。等腰直角三角形的两个底角分别是多少度?
6、如图,在以点A为圆心的两个同心圆中,
一条直线与这两个同心圆分别相交于B,E,D,C
四个点。请找出图中相等的线段和相等的角,
并说明理由挑战自我 如图2-42,在Rt△ABC中,∠C=90o,把直角边BC沿过点B的某条直线折叠,使点C落到斜边AB上的一点D处,当∠A为多少度时,点D恰为AB的中点?说明你的结论。等腰三角形1、等腰三角形是轴对称图形,等腰三角形的对称轴是底边的垂直平分线。2、等腰三角形的顶角平分线,底边上的高、底边上的中线重合(三线合一)课堂小结3、等腰三角形的两个底角相等。课堂练习练习一
1、下列图形中,不是轴对称图形的是( )
A. 等腰三角形 B. 线段
C. 钝角 D. 直角三角形
2、等腰三角形的底角是顶角的2倍,则底角度数为( )
A. 36° B. 32° C. 64° D. 72°
3、等腰三角形的对称轴是___________ 。DD底边的垂直平分线4、分别找出如图所示中各个图形的对称轴。练习二、
1、等腰三角形底边上的高与一腰所成的角等于( )
A. 顶角 B. 顶角的一半
C. 顶角的两倍 D. 底角的一半
2、等腰三角形两边的长分别为2cm和5cm,则这个三角形的周长是( )
A. 9cm B. 12cm
C. 9cm或12cm D. 在9cm与12cm之间课堂练习3、如图,等腰△ABC中,AD⊥BC于D,已知DC=2cm,AB=3cm,则△ABC的周长为___________。4、已知:等腰三角形的一个角是80°,则它的另外两个角是 。ABCDBB10cm50°、50°或80°、20°作业习题1、5 惜时如金
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
