12.2.1三角形全等的判定(1)SSS ——课件
文档属性
| 名称 | 12.2.1三角形全等的判定(1)SSS ——课件 |  | |
| 格式 | zip | ||
| 文件大小 | 164.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-17 16:54:52 | ||
图片预览




文档简介
(共20张PPT)
12.2三角形全等的判定(1)SSS
学习目标:
掌握并识记三角形全等的判定定理——SSS,并能正确运用SSS定理证明三角形全等。
认真看课本(P35——P37练习之前),
1.思考“探究1”和“探究2”中的问题,通过画图来回答。
2.注意“黄色书签”的提示(并会正确运用)和思考“云图”中的问题。
3.注意P36例1的解题格式和步骤,思考运用SSS定理需要哪些条件,如何正确书写两个三角形全等的步骤。
如有疑问,立即举手问老师。
6分钟后,比谁能正确的运用SSS定理做对检测题。
自学指导:
A
B
C
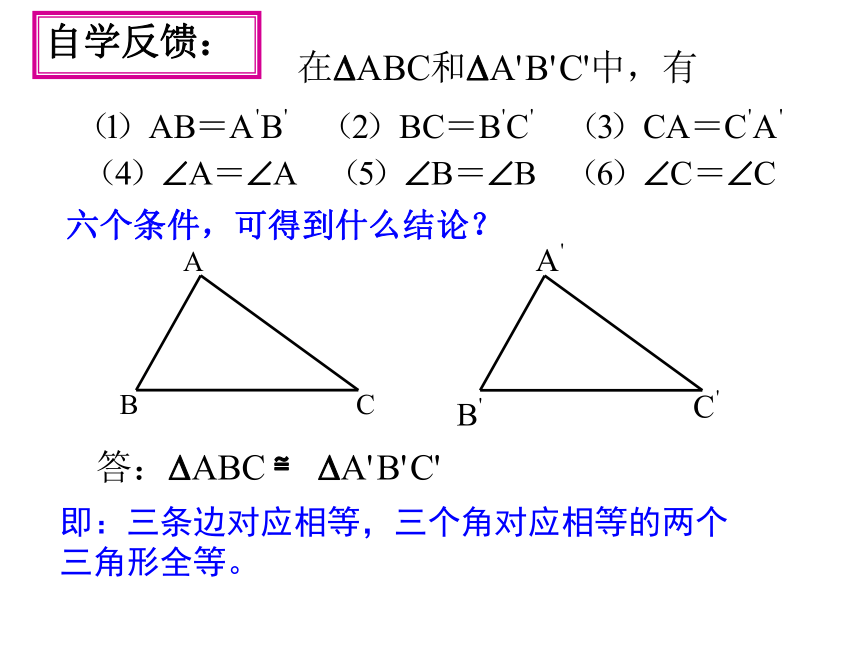
即:三条边对应相等,三个角对应相等的两个三角形全等。
六个条件,可得到什么结论?
≌
自学反馈:
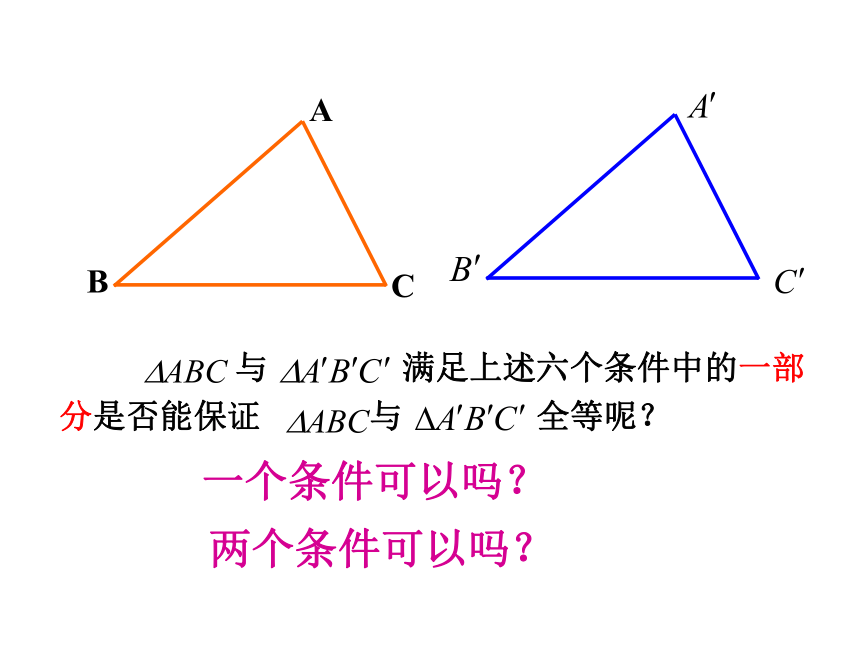
与 满足上述六个条件中的一部分是否能保证 与 全等呢?
A
B
C
一个条件可以吗?
两个条件可以吗?
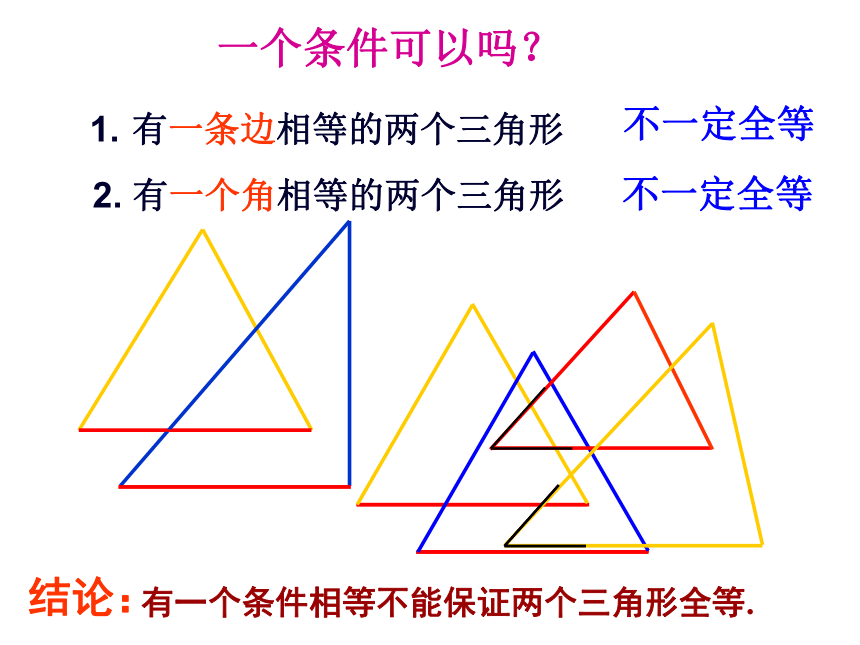
一个条件可以吗?
有一条边相等的两个三角形
不一定全等
2. 有一个角相等的两个三角形
不一定全等
结论:
有一个条件相等不能保证两个三角形全等.
6cm
300
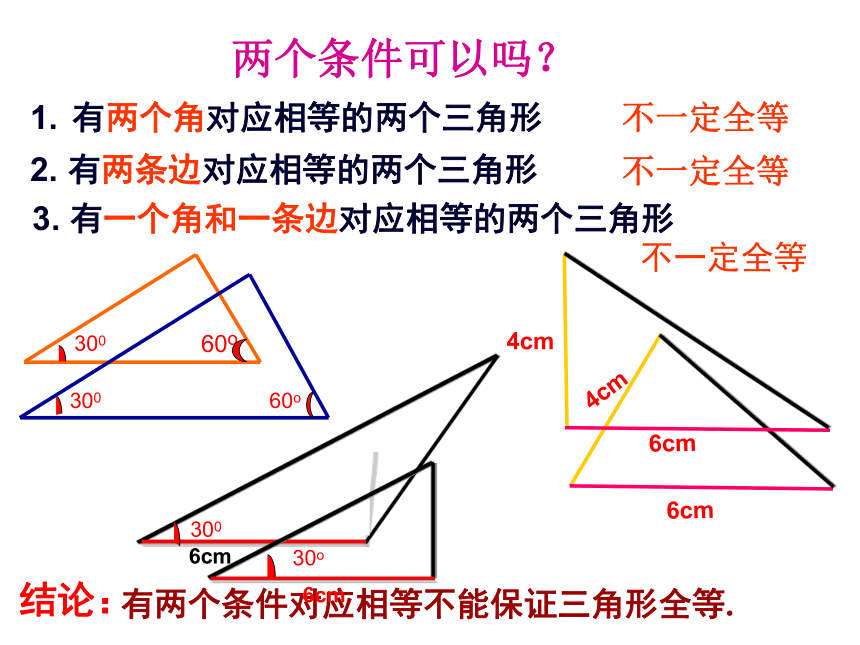
有两个条件对应相等不能保证三角形全等.
60o
300
不一定全等
有两个角对应相等的两个三角形
两个条件可以吗?
3. 有一个角和一条边对应相等的两个三角形
2. 有两条边对应相等的两个三角形
4cm
6cm
不一定全等
300
60o
4cm
6cm
不一定全等
30o
6cm
结论:
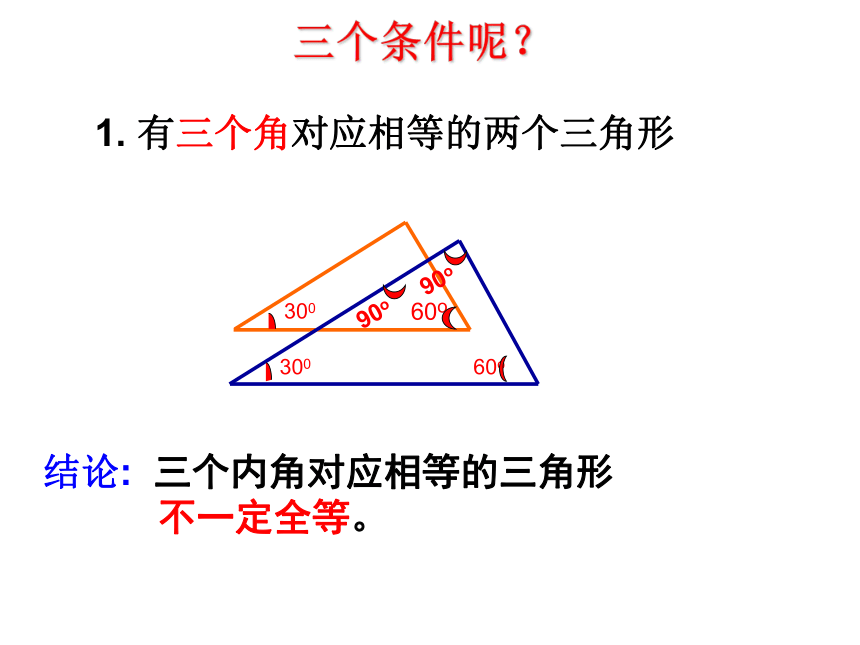
三个条件呢?
三个角;
2. 三条边;
3. 两边一角;
4. 两角一边。
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
结论: 三个内角对应相等的三角形
不一定全等。
有三个角对应相等的两个三角形
60o
300
300
60o
90o
90o
三个条件呢?
三边相等的两个三角形会全等吗?
画法:
你能得出什么结论?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
用上面的结论可以判定两个三角形全等.
判断两个三角形全等的推理过程,叫做证明三角形全等.
A
B
C
A
B
C
三边对应相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢
≌
结论
∴ ∠A = ∠___
∠B = ∠___
∠C = ∠___
①准备条件:
证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
归纳:
P37:练习 1、2
要求:1.仿照例题格式、步骤。
2.字迹工整。
检测题:
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
课堂小结:
必做题:P43:习题12.2 :1
选做题:P44: 9
当堂训练:
如图,在四边形ABCD中, AB=CD,
AD=CB, 求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△CDB(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A=∠C (全等三角形的对应角相等)
你能说明AB∥CD,AD∥BC吗?
补充练习:
补充练习:
补充练习:
补充练习:
12.2三角形全等的判定(1)SSS
学习目标:
掌握并识记三角形全等的判定定理——SSS,并能正确运用SSS定理证明三角形全等。
认真看课本(P35——P37练习之前),
1.思考“探究1”和“探究2”中的问题,通过画图来回答。
2.注意“黄色书签”的提示(并会正确运用)和思考“云图”中的问题。
3.注意P36例1的解题格式和步骤,思考运用SSS定理需要哪些条件,如何正确书写两个三角形全等的步骤。
如有疑问,立即举手问老师。
6分钟后,比谁能正确的运用SSS定理做对检测题。
自学指导:
A
B
C
即:三条边对应相等,三个角对应相等的两个三角形全等。
六个条件,可得到什么结论?
≌
自学反馈:
与 满足上述六个条件中的一部分是否能保证 与 全等呢?
A
B
C
一个条件可以吗?
两个条件可以吗?
一个条件可以吗?
有一条边相等的两个三角形
不一定全等
2. 有一个角相等的两个三角形
不一定全等
结论:
有一个条件相等不能保证两个三角形全等.
6cm
300
有两个条件对应相等不能保证三角形全等.
60o
300
不一定全等
有两个角对应相等的两个三角形
两个条件可以吗?
3. 有一个角和一条边对应相等的两个三角形
2. 有两条边对应相等的两个三角形
4cm
6cm
不一定全等
300
60o
4cm
6cm
不一定全等
30o
6cm
结论:
三个条件呢?
三个角;
2. 三条边;
3. 两边一角;
4. 两角一边。
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
结论: 三个内角对应相等的三角形
不一定全等。
有三个角对应相等的两个三角形
60o
300
300
60o
90o
90o
三个条件呢?
三边相等的两个三角形会全等吗?
画法:
你能得出什么结论?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
用上面的结论可以判定两个三角形全等.
判断两个三角形全等的推理过程,叫做证明三角形全等.
A
B
C
A
B
C
三边对应相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢
≌
结论
∴ ∠A = ∠___
∠B = ∠___
∠C = ∠___
①准备条件:
证全等时要用的间接条件要先证好;
②三角形全等书写三步骤:
写出在哪两个三角形中
摆出三个条件用大括号括起来
写出全等结论
证明的书写步骤:
归纳:
P37:练习 1、2
要求:1.仿照例题格式、步骤。
2.字迹工整。
检测题:
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
课堂小结:
必做题:P43:习题12.2 :1
选做题:P44: 9
当堂训练:
如图,在四边形ABCD中, AB=CD,
AD=CB, 求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△CDB(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A=∠C (全等三角形的对应角相等)
你能说明AB∥CD,AD∥BC吗?
补充练习:
补充练习:
补充练习:
补充练习:
