山东省泰安市宁阳县(五四学制)2022-2023学年八年级下学期期末数学试题(无答案)
文档属性
| 名称 | 山东省泰安市宁阳县(五四学制)2022-2023学年八年级下学期期末数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 825.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-05 10:36:33 | ||
图片预览

文档简介
2022-2023学年度第二学期期末质量检测
八年级数学试题
满分150分 时间120分钟
一、选择题(每小题4分,共48分)
1.要使式子有意义,则的取值范围是( )
A. B. C.且 D.且
2.如图,在平面直角坐标系中,菱形的顶点,,顶点在轴正半轴上,则点的坐标为( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.若关于的一元二次方程的一个根为,则的值为( )
A.0 B.1 C.或0 D.0或1
5.如图,在三角形纸片中,,,,沿虚线剪下的涂色部分的三角形与相似的是( )
A. B. C. D.
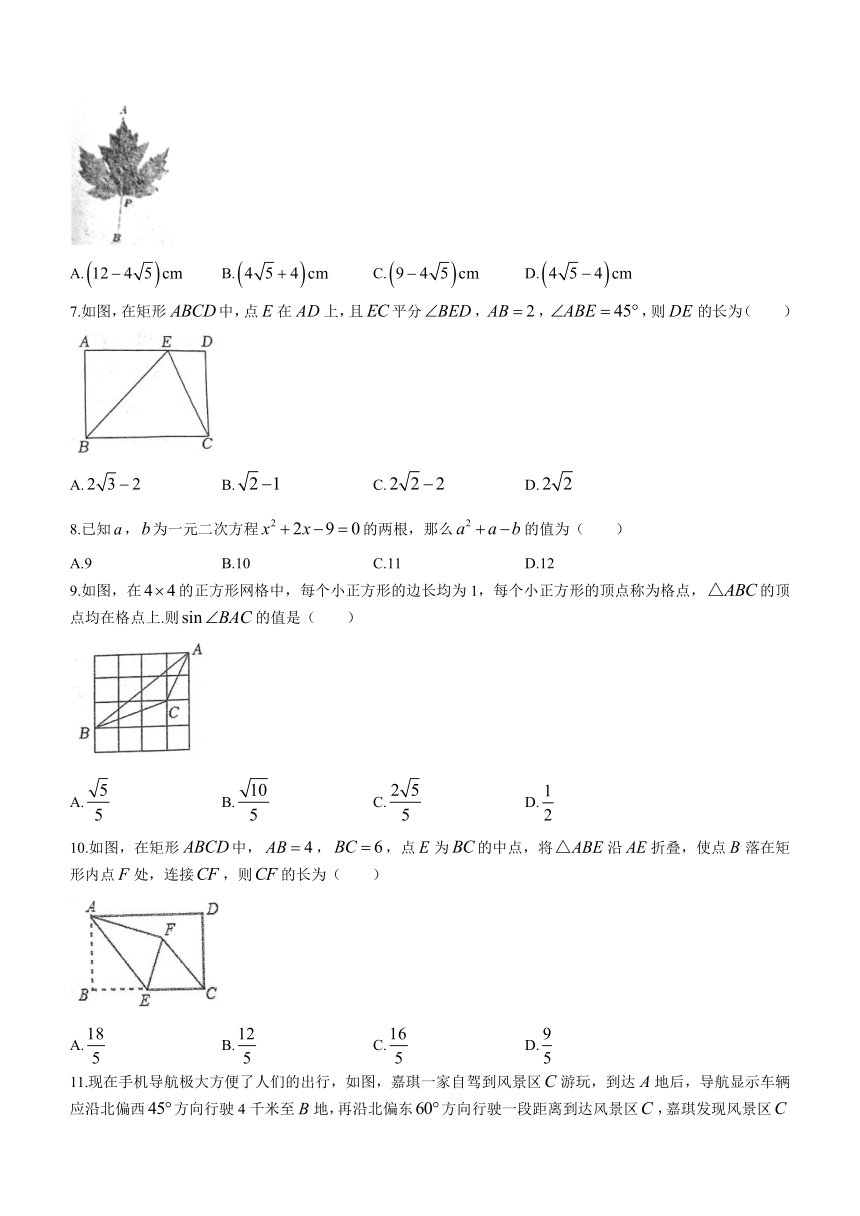
6.大自然巧夺天工,一片树叶也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是( )
A. B. C. D.
7.如图,在矩形中,点在上,且平分,,,则的长为( )
A. B. C. D.
8.已知,为一元二次方程的两根,那么的值为( )
A.9 B.10 C.11 D.12
9.如图,在的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,的顶点均在格点上.则的值是( )
A. B. C. D.
10.如图,在矩形中,,,点为的中点,将沿折叠,使点落在矩形内点处,连接,则的长为( )
A. B. C. D.
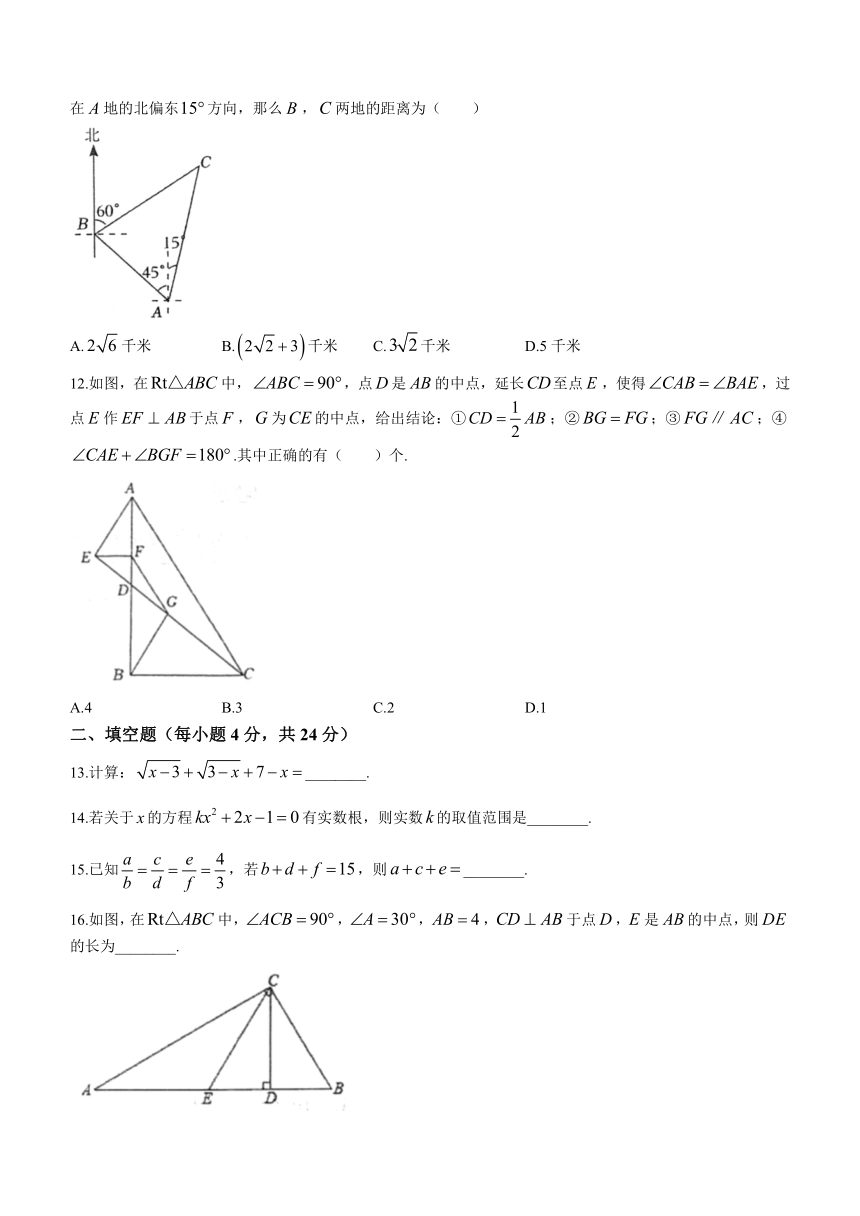
11.现在手机导航极大方便了人们的出行,如图,嘉琪一家自驾到风景区游玩,到达地后,导航显示车辆应沿北偏西方向行驶4千米至地,再沿北偏东方向行驶一段距离到达风景区,嘉琪发现风景区在地的北偏东方向,那么,两地的距离为( )
A.千米 B.千米 C.千米 D.5千米
12.如图,在中,,点是的中点,延长至点,使得,过点作于点,为的中点,给出结论:①;②;③;④.其中正确的有( )个.
A.4 B.3 C.2 D.1
二、填空题(每小题4分,共24分)
13.计算:________.
14.若关于的方程有实数根,则实数的取值范围是________.
15.已知,若,则________.
16.如图,在中,,,,于点,是的中点,则的长为________.
17.如图,菱形的对角线相交于点,,,点为边上一点,且不与点、重合.过作于,于,连接,则的最小值等于________.
18.如图,,,,,在边上取点,使得与相似,则线段的长为________.
三、解答题
19.(12分)计算下列各题:
(1); (2).
(3)
20.(8分)用适当的方法解下列方程:
(1); (2);
21.(10分)王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树的高度,他在点处测得大树顶端的仰角为,再从点出发沿斜坡走米到达斜坡上点,在点处测得树顶端的仰角为,若斜坡的坡比为(点、、在同一水平线上).
(1)求王刚同学从点到点的过程中上升的高度;
(2)求大树的高度(结果保留根号).
22.(10分)某种商品的标价为200元/件,由于换季的影响,销量不佳,店家经过两次降价后的价格为128元/件,并且两资助降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为80元/件,若以128元/件售出,平均每天能售出20件,另外每天需支付其他各种费用100元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,如果每天盈利1475元,每件应降价多少元?
23.(12分)如图,菱形的对角线与交于点,于点,交于点,于点.
(1)判断四边形的形状,并写出证明过程.
(2)若,,求的长.
24.(12分)如图,在中,,于,作于,是中点,连交于点.
(1)求证:;
(2)若,,求的值.
25.(14分)已知点是线段的中点,点是直线上的任意一点,分别过点和点作直线的垂线,垂足分别为点和点,我们定义垂足与中点之间的距离为“足中距”.
(1)【猜想验证】如图1,当点与点重合时,请你猜想、验证后直接写出“足中距”和的数量关系是________.
(2)【探究证明】如图2,当点是线段上的任意一点时,“足中距”和的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)【拓展延伸】如图3,①当点是线段延长线上的任意一点时,“足中距”和的数量关系是否依次成立,若成立,请给出证明;若不成立,请说明理由;
②若,求证:.
八年级数学试题
满分150分 时间120分钟
一、选择题(每小题4分,共48分)
1.要使式子有意义,则的取值范围是( )
A. B. C.且 D.且
2.如图,在平面直角坐标系中,菱形的顶点,,顶点在轴正半轴上,则点的坐标为( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.若关于的一元二次方程的一个根为,则的值为( )
A.0 B.1 C.或0 D.0或1
5.如图,在三角形纸片中,,,,沿虚线剪下的涂色部分的三角形与相似的是( )
A. B. C. D.
6.大自然巧夺天工,一片树叶也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么的长度是( )
A. B. C. D.
7.如图,在矩形中,点在上,且平分,,,则的长为( )
A. B. C. D.
8.已知,为一元二次方程的两根,那么的值为( )
A.9 B.10 C.11 D.12
9.如图,在的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点称为格点,的顶点均在格点上.则的值是( )
A. B. C. D.
10.如图,在矩形中,,,点为的中点,将沿折叠,使点落在矩形内点处,连接,则的长为( )
A. B. C. D.
11.现在手机导航极大方便了人们的出行,如图,嘉琪一家自驾到风景区游玩,到达地后,导航显示车辆应沿北偏西方向行驶4千米至地,再沿北偏东方向行驶一段距离到达风景区,嘉琪发现风景区在地的北偏东方向,那么,两地的距离为( )
A.千米 B.千米 C.千米 D.5千米
12.如图,在中,,点是的中点,延长至点,使得,过点作于点,为的中点,给出结论:①;②;③;④.其中正确的有( )个.
A.4 B.3 C.2 D.1
二、填空题(每小题4分,共24分)
13.计算:________.
14.若关于的方程有实数根,则实数的取值范围是________.
15.已知,若,则________.
16.如图,在中,,,,于点,是的中点,则的长为________.
17.如图,菱形的对角线相交于点,,,点为边上一点,且不与点、重合.过作于,于,连接,则的最小值等于________.
18.如图,,,,,在边上取点,使得与相似,则线段的长为________.
三、解答题
19.(12分)计算下列各题:
(1); (2).
(3)
20.(8分)用适当的方法解下列方程:
(1); (2);
21.(10分)王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树的高度,他在点处测得大树顶端的仰角为,再从点出发沿斜坡走米到达斜坡上点,在点处测得树顶端的仰角为,若斜坡的坡比为(点、、在同一水平线上).
(1)求王刚同学从点到点的过程中上升的高度;
(2)求大树的高度(结果保留根号).
22.(10分)某种商品的标价为200元/件,由于换季的影响,销量不佳,店家经过两次降价后的价格为128元/件,并且两资助降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为80元/件,若以128元/件售出,平均每天能售出20件,另外每天需支付其他各种费用100元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售出5件,如果每天盈利1475元,每件应降价多少元?
23.(12分)如图,菱形的对角线与交于点,于点,交于点,于点.
(1)判断四边形的形状,并写出证明过程.
(2)若,,求的长.
24.(12分)如图,在中,,于,作于,是中点,连交于点.
(1)求证:;
(2)若,,求的值.
25.(14分)已知点是线段的中点,点是直线上的任意一点,分别过点和点作直线的垂线,垂足分别为点和点,我们定义垂足与中点之间的距离为“足中距”.
(1)【猜想验证】如图1,当点与点重合时,请你猜想、验证后直接写出“足中距”和的数量关系是________.
(2)【探究证明】如图2,当点是线段上的任意一点时,“足中距”和的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)【拓展延伸】如图3,①当点是线段延长线上的任意一点时,“足中距”和的数量关系是否依次成立,若成立,请给出证明;若不成立,请说明理由;
②若,求证:.
同课章节目录
