数学人教A版(2019)必修第二册9.2.3总体集中趋势的估计 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册9.2.3总体集中趋势的估计 课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
9.2.3 总体集中趋势的估计
人教版高中数学必修第二册(A版)
一.情景导入
求职者小范
这个公司员工收入到底怎样?
赵经理
第二天,小范哼着小歌上班了.
我们好几个人
工资都是5000元
技术员D
技术员C
我的工资是6000元,在公司算中等收入
我这里报酬不错, 月平均工资是9000元,你在这里好好干!
场景1--小范求职
①
②
③
④
一.情景导入
小范在公司工作了一周后
经理,你忽悠了我,我已问过其他技术员,没有一个技术员的工资超过9000元.
平均工资确实是每月9000元,你看看公司的工资报表.
场景2--小范的疑惑
①
②
一.情景导入
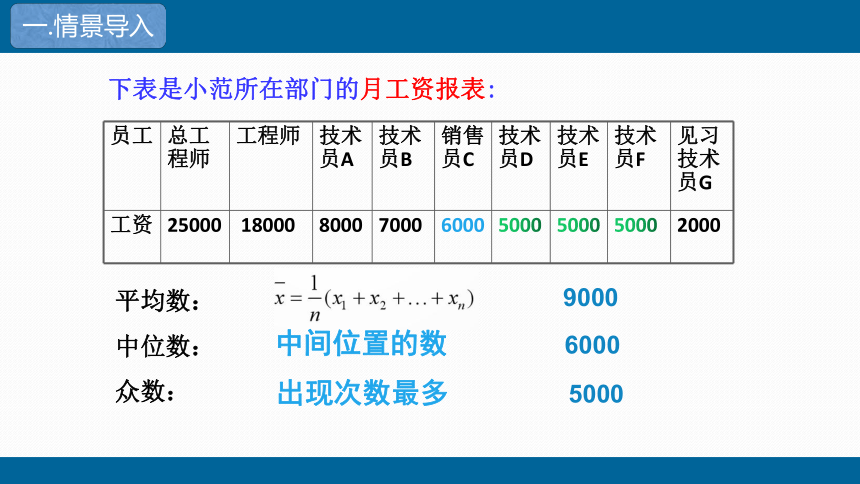
下表是小范所在部门的月工资报表:
员工 总工程师 工程师 技术员A 技术员B 销售员C 技术员D 技术员E 技术员F 见习技术员G
工资 25000 18000 8000 7000 6000 5000 5000 5000 2000
平均数:
中位数:
众数:
9000
6000
5000
中间位置的数
出现次数最多
我的工资是6000元,在公司算中等收入
我们好几个人工资都是5000元
技术员D
技术员C
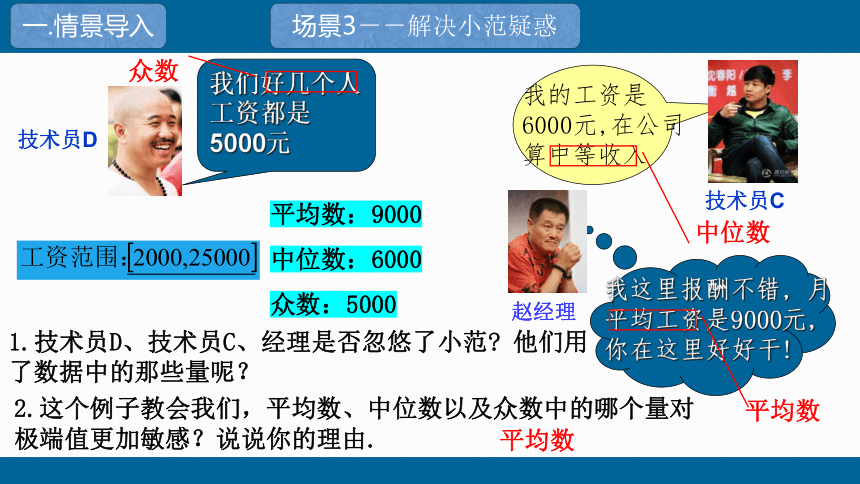
1.技术员D、技术员C、经理是否忽悠了小范 他们用了数据中的那些量呢?
众数
中位数
一.情景导入
2.这个例子教会我们,平均数、中位数以及众数中的哪个量对极端值更加敏感?说说你的理由.
我这里报酬不错, 月平均工资是9000元,你在这里好好干!
平均数
平均数:9000
中位数:6000
众数:5000
赵经理
场景3--解决小范疑惑
平均数
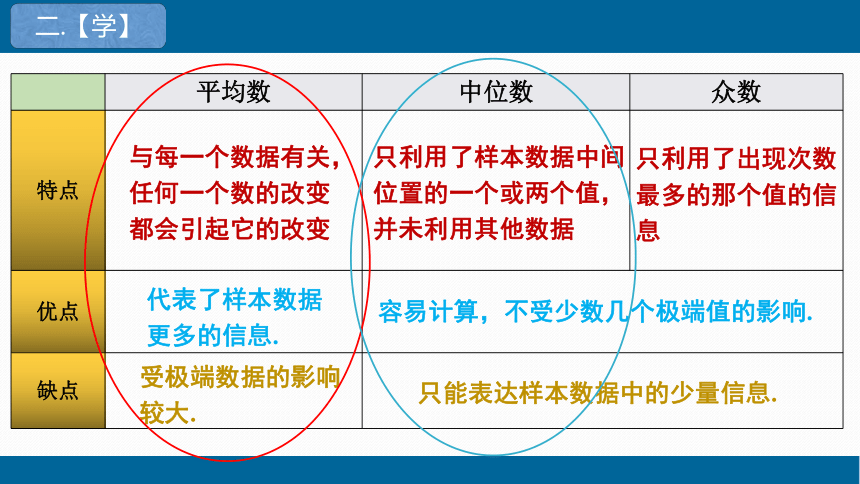
平均数 中位数 众数
特点
优点 缺点 与每一个数据有关,任何一个数的改变都会引起它的改变
只利用了样本数据中间位置的一个或两个值,并未利用其他数据
只利用了出现次数最多的那个值的信息
受极端数据的影响较大.
代表了样本数据更多的信息.
只能表达样本数据中的少量信息.
容易计算,不受少数几个极端值的影响.
二.【学】
二.【学】
本次100名学生周测的成绩如图,假设每组分数用该组的中间值来估计,如何求本次周测的平均数
成绩分组 频率
[40,60) 0.2
[60,80) 0.5
[80,100] 0.3
合计 1.00
追问:如果不知道样本容量,还能求出平均数吗
频率
样本总量
频数
平均数=每组组中值×频率之和
任务一
成绩分组组中值 频率
x1 f1
x2 f2
x3 f3
... ...
xn-1 fn-1
xn fn
合计 1.00
类比刚才的运算过程,你可以推算出下表的平均数计算公式吗?
二.【学】
任务二
问题1 小范拿到公司本月月均销售额的频率分布直方图(假设组内数据均匀分布),公司预定目标为人均销售额8.5万元,请问本月是否达成目标?
频率/组距
月销售额/万元
任务三.平均数的估计
二.【学】
问题一:类比任务二的推导公式,用文字语言描述频率分布直方图中平均数的计算?
问题二:通过计算数据,判断是否达标?
平均数:每个小矩形的面积乘以小矩形底边中点的横坐标之和.
频率/组距
月销售额/万元
8.9
任务三.平均数的估计
二.【学】
8.9>8.5 已达标
问题2 该样本中的众数是多少?
频率/组距
月销售额/万元
任务四.众数的估计
众数:最高矩形的中点的横坐标.
二.【学】
问题3 由于达成预定目标,公司决定给销售额更高的半数员工发放奖金,请问:月销售额达到多少万元即可获得奖金
频率/组距
月销售额/万元
任务五.中位数的估计
中位数:把频率分布直方图划分左右面积相等的分界线与x轴交点的横坐标
二.【学】
中位数
即求50%分位数
三.【究】
小组合作探究
探究:小范所在公司的工资分布情况的频率分布直方图大概符合下列哪一种情况?
问题一:三种情况的平均数和中位数分别是多少?
问题二:总结平均数和中位数有什么分布规律?
(1)
(2)
(3)
问题三:由此可知,小范所在公司的工资分布情况属于哪一种?
三.【究】
小组合作探究
(1)
(2)
(3)
平均数和中位数都是8
平均数是7.6 中位数约为7.3
平均数是8.4 中位数约为8.6
(1)直方图形状对称:
(2)直方图右边“拖尾”:
(3)直方图左边“拖尾”:
平均数和中位数应该大体上差不多;
平均数大于中位数;
平均数小于中位数.
与中位数相比,平均数总在直方图的“长尾巴”那边
(2022·全国·高一专题练均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关,在下图两种分布形态中,分别对应平均数和中位数之一,则可能的对应关系是( )A. a为中位数,b为平均数,c为平均数,d为中位数B. a为平均数,b为中位数,c为平均数,d为中位数C. a为中位数,b为平均数,c为中位数,d为平均数D. a为平均数,b为中位数,c为中位数,d为平均数
A
四.【练】
当堂训练一
(2023·全国模拟)为支持“中小型企业”的发展,某市决定对部分企业的税收进行适当减免,现调查了当地100家中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,则下面结论正确的是( )
A.ɑ的值为0.0016
B.样本的中位数是400万元
C.估计当地中小型企业年收入的平均数是400万元
D.样本在区间[500,700]内的频数为18
例1
D
四.【练】
当堂训练二
解析:D
对于A 由题意知0.001×100+0.002×100+0.002 6×100×2+100a+0.000 4×100=1,解得a=0.001 4,故A错误;
对于B 0.001×100+0.002×100=0.3<0.5,0.3+0.002 6×100=0.56>0.5,可知中位数位于[300,400]内,故B错误;
对于C 样本的平均数150×0.1+250×0.2+350×0.26+450×0.26+550×0.14+650×0.04=376<400,故C错误;
对于D 样本在[500,700]内的频率为(0.001 4+0.000 4)×100=0.18,故频数为0.18×100=18,故D正确.
某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100)后,画出如图所示的频率分布直方图.估计这次考试的及格率(60分及以上为及格)为________;平均分为________
四.【练】
当堂训练三
75%
71
课堂小结
课后作业:
作业一(必做):练习1,2题
作业二(选做):思考统计学在生活中的应用
总体集中趋势的估计
温故而知新,让我们回顾下,今天学习了哪些新知识?
平均数:每个小矩形的面积乘以小矩形底边中点的横坐标之和。
中位数:左边和右边的直方图的面积各为0.5,
即中位数左右的面积相等.
众数:最高矩形的中点的横坐标.
拓展思维
统计学的应用(诺曼底登陆)
用
于
生
活
源
于
生
活
数学
数学
1.某校从参加高一年级期末考试的学生中抽出60名,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图中的信息,回答下列问题:
(1)估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
五.【测】
众数是频率分布直方图中最高小矩
形底边中点的横坐标,所以众数为
m=75.0.
前3个小矩形面积和为0.01×10
+0.015×10+0.015×10=0.4<0.5,
前4个小矩形面积和为0.4+0.03×10=0.7>0.5,
依题意,60及60以上的分数在第三、
四、五、六组,频率和为(0.015+0.03
+0.025+0.005)×10=0.75,
所以估计这次考试的物理成绩的及格率是75%.
利用组中值估算抽样学生的平均分为45×f1+55×f2+65×f3+75×f4+85×f5+95×f6=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
所以估计这次考试的物理成绩的平均分是71分.
(2023·山东青岛二模)某学校调查了高三1000名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,以下结论不正确的是( )
A.估计这1000名学生中每周的自习时间不少于25小时的人数是300
B.估计这1000名学生每周的自习时间的众数是23.85
C.估计这1000名学生每周的自习时间的中位数是23.75
D.估计这1000名学生每周的自习时间的平均数是23.875
B
四.【练】
当堂训练二
解析:B
对于A (0.08+0.04)×2.5=0.3,0.3×1 000=300,故选项A正确.
对于B (22.5+25)÷2=23.75,故选项B错误;
对于C 设中位数为x,则有0.02×2.5+0.1×2.5+(x-22.5)×0.16=0.5,解得x=23.75,故选项C正确;
对于D 0.02×2.5×18.75+0.1×2.5×21.250.16×2.5×23.75+0.08×2.5×26.25+0.04×2.5×28.75=23.875,故选项D正确.
9.2.3 总体集中趋势的估计
人教版高中数学必修第二册(A版)
一.情景导入
求职者小范
这个公司员工收入到底怎样?
赵经理
第二天,小范哼着小歌上班了.
我们好几个人
工资都是5000元
技术员D
技术员C
我的工资是6000元,在公司算中等收入
我这里报酬不错, 月平均工资是9000元,你在这里好好干!
场景1--小范求职
①
②
③
④
一.情景导入
小范在公司工作了一周后
经理,你忽悠了我,我已问过其他技术员,没有一个技术员的工资超过9000元.
平均工资确实是每月9000元,你看看公司的工资报表.
场景2--小范的疑惑
①
②
一.情景导入
下表是小范所在部门的月工资报表:
员工 总工程师 工程师 技术员A 技术员B 销售员C 技术员D 技术员E 技术员F 见习技术员G
工资 25000 18000 8000 7000 6000 5000 5000 5000 2000
平均数:
中位数:
众数:
9000
6000
5000
中间位置的数
出现次数最多
我的工资是6000元,在公司算中等收入
我们好几个人工资都是5000元
技术员D
技术员C
1.技术员D、技术员C、经理是否忽悠了小范 他们用了数据中的那些量呢?
众数
中位数
一.情景导入
2.这个例子教会我们,平均数、中位数以及众数中的哪个量对极端值更加敏感?说说你的理由.
我这里报酬不错, 月平均工资是9000元,你在这里好好干!
平均数
平均数:9000
中位数:6000
众数:5000
赵经理
场景3--解决小范疑惑
平均数
平均数 中位数 众数
特点
优点 缺点 与每一个数据有关,任何一个数的改变都会引起它的改变
只利用了样本数据中间位置的一个或两个值,并未利用其他数据
只利用了出现次数最多的那个值的信息
受极端数据的影响较大.
代表了样本数据更多的信息.
只能表达样本数据中的少量信息.
容易计算,不受少数几个极端值的影响.
二.【学】
二.【学】
本次100名学生周测的成绩如图,假设每组分数用该组的中间值来估计,如何求本次周测的平均数
成绩分组 频率
[40,60) 0.2
[60,80) 0.5
[80,100] 0.3
合计 1.00
追问:如果不知道样本容量,还能求出平均数吗
频率
样本总量
频数
平均数=每组组中值×频率之和
任务一
成绩分组组中值 频率
x1 f1
x2 f2
x3 f3
... ...
xn-1 fn-1
xn fn
合计 1.00
类比刚才的运算过程,你可以推算出下表的平均数计算公式吗?
二.【学】
任务二
问题1 小范拿到公司本月月均销售额的频率分布直方图(假设组内数据均匀分布),公司预定目标为人均销售额8.5万元,请问本月是否达成目标?
频率/组距
月销售额/万元
任务三.平均数的估计
二.【学】
问题一:类比任务二的推导公式,用文字语言描述频率分布直方图中平均数的计算?
问题二:通过计算数据,判断是否达标?
平均数:每个小矩形的面积乘以小矩形底边中点的横坐标之和.
频率/组距
月销售额/万元
8.9
任务三.平均数的估计
二.【学】
8.9>8.5 已达标
问题2 该样本中的众数是多少?
频率/组距
月销售额/万元
任务四.众数的估计
众数:最高矩形的中点的横坐标.
二.【学】
问题3 由于达成预定目标,公司决定给销售额更高的半数员工发放奖金,请问:月销售额达到多少万元即可获得奖金
频率/组距
月销售额/万元
任务五.中位数的估计
中位数:把频率分布直方图划分左右面积相等的分界线与x轴交点的横坐标
二.【学】
中位数
即求50%分位数
三.【究】
小组合作探究
探究:小范所在公司的工资分布情况的频率分布直方图大概符合下列哪一种情况?
问题一:三种情况的平均数和中位数分别是多少?
问题二:总结平均数和中位数有什么分布规律?
(1)
(2)
(3)
问题三:由此可知,小范所在公司的工资分布情况属于哪一种?
三.【究】
小组合作探究
(1)
(2)
(3)
平均数和中位数都是8
平均数是7.6 中位数约为7.3
平均数是8.4 中位数约为8.6
(1)直方图形状对称:
(2)直方图右边“拖尾”:
(3)直方图左边“拖尾”:
平均数和中位数应该大体上差不多;
平均数大于中位数;
平均数小于中位数.
与中位数相比,平均数总在直方图的“长尾巴”那边
(2022·全国·高一专题练均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关,在下图两种分布形态中,分别对应平均数和中位数之一,则可能的对应关系是( )A. a为中位数,b为平均数,c为平均数,d为中位数B. a为平均数,b为中位数,c为平均数,d为中位数C. a为中位数,b为平均数,c为中位数,d为平均数D. a为平均数,b为中位数,c为中位数,d为平均数
A
四.【练】
当堂训练一
(2023·全国模拟)为支持“中小型企业”的发展,某市决定对部分企业的税收进行适当减免,现调查了当地100家中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,则下面结论正确的是( )
A.ɑ的值为0.0016
B.样本的中位数是400万元
C.估计当地中小型企业年收入的平均数是400万元
D.样本在区间[500,700]内的频数为18
例1
D
四.【练】
当堂训练二
解析:D
对于A 由题意知0.001×100+0.002×100+0.002 6×100×2+100a+0.000 4×100=1,解得a=0.001 4,故A错误;
对于B 0.001×100+0.002×100=0.3<0.5,0.3+0.002 6×100=0.56>0.5,可知中位数位于[300,400]内,故B错误;
对于C 样本的平均数150×0.1+250×0.2+350×0.26+450×0.26+550×0.14+650×0.04=376<400,故C错误;
对于D 样本在[500,700]内的频率为(0.001 4+0.000 4)×100=0.18,故频数为0.18×100=18,故D正确.
某校举行了由全部学生参加的校园安全知识考试,从中抽出60名学生,将其成绩分成六段[40,50),[50,60),…,[90,100)后,画出如图所示的频率分布直方图.估计这次考试的及格率(60分及以上为及格)为________;平均分为________
四.【练】
当堂训练三
75%
71
课堂小结
课后作业:
作业一(必做):练习1,2题
作业二(选做):思考统计学在生活中的应用
总体集中趋势的估计
温故而知新,让我们回顾下,今天学习了哪些新知识?
平均数:每个小矩形的面积乘以小矩形底边中点的横坐标之和。
中位数:左边和右边的直方图的面积各为0.5,
即中位数左右的面积相等.
众数:最高矩形的中点的横坐标.
拓展思维
统计学的应用(诺曼底登陆)
用
于
生
活
源
于
生
活
数学
数学
1.某校从参加高一年级期末考试的学生中抽出60名,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后,画出如图所示的频率分布直方图.观察图中的信息,回答下列问题:
(1)估计这次考试的物理成绩的众数m与中位数n(结果保留一位小数);
(2)估计这次考试的物理成绩的及格率(60分及以上为及格)和平均分.
五.【测】
众数是频率分布直方图中最高小矩
形底边中点的横坐标,所以众数为
m=75.0.
前3个小矩形面积和为0.01×10
+0.015×10+0.015×10=0.4<0.5,
前4个小矩形面积和为0.4+0.03×10=0.7>0.5,
依题意,60及60以上的分数在第三、
四、五、六组,频率和为(0.015+0.03
+0.025+0.005)×10=0.75,
所以估计这次考试的物理成绩的及格率是75%.
利用组中值估算抽样学生的平均分为45×f1+55×f2+65×f3+75×f4+85×f5+95×f6=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
所以估计这次考试的物理成绩的平均分是71分.
(2023·山东青岛二模)某学校调查了高三1000名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,以下结论不正确的是( )
A.估计这1000名学生中每周的自习时间不少于25小时的人数是300
B.估计这1000名学生每周的自习时间的众数是23.85
C.估计这1000名学生每周的自习时间的中位数是23.75
D.估计这1000名学生每周的自习时间的平均数是23.875
B
四.【练】
当堂训练二
解析:B
对于A (0.08+0.04)×2.5=0.3,0.3×1 000=300,故选项A正确.
对于B (22.5+25)÷2=23.75,故选项B错误;
对于C 设中位数为x,则有0.02×2.5+0.1×2.5+(x-22.5)×0.16=0.5,解得x=23.75,故选项C正确;
对于D 0.02×2.5×18.75+0.1×2.5×21.250.16×2.5×23.75+0.08×2.5×26.25+0.04×2.5×28.75=23.875,故选项D正确.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
