第三单元第6课时《单元综合复习》表格式精品教案 数学北师大版 五年级上册
文档属性
| 名称 | 第三单元第6课时《单元综合复习》表格式精品教案 数学北师大版 五年级上册 | 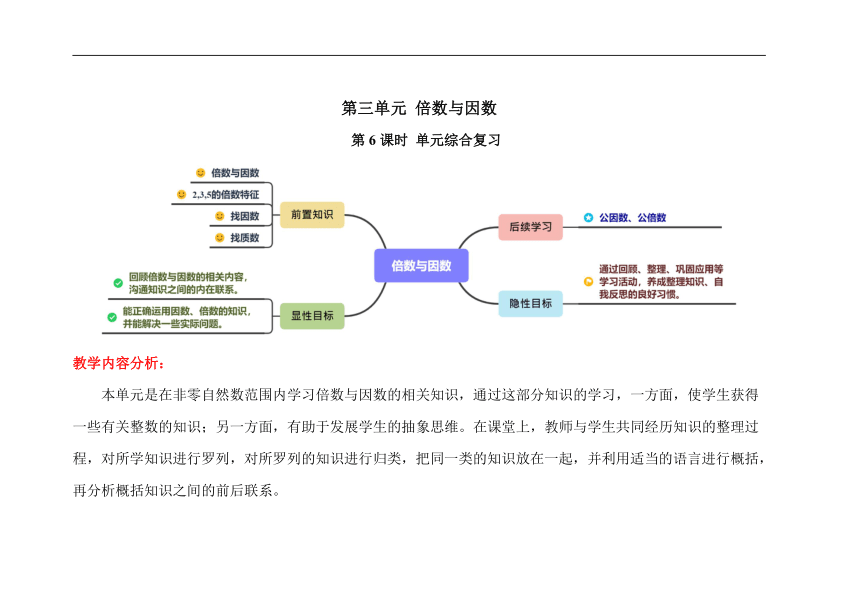 | |
| 格式 | docx | ||
| 文件大小 | 594.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 17:23:27 | ||
图片预览




文档简介
第三单元 倍数与因数
第6课时 单元综合复习
教学内容分析:
本单元是在非零自然数范围内学习倍数与因数的相关知识,通过这部分知识的学习,一方面,使学生获得一些有关整数的知识;另一方面,有助于发展学生的抽象思维。在课堂上,教师与学生共同经历知识的整理过程,对所学知识进行罗列,对所罗列的知识进行归类,把同一类的知识放在一起,并利用适当的语言进行概括,再分析概括知识之间的前后联系。
教学目标:
1.回顾倍数与因数的相关内容,沟通知识之间的内在联系。
2.能正确运用因数、倍数的知识,并能解决一些实际问题。
3.通过回顾、整理、巩固应用等学习活动,养成整理知识、自我反思的良好习惯。
教学重点:
理解各个概念,分析各个概念之间的联系与区别。
教学难点:
应用所学知识解决实际问题。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 知识梳理 师:同学们,在这个单元中,我们都学习了哪些知识,请你翻翻数学书,一起来说一说。 师:下面我们就来一起回顾下,具体学习了什么。 1.倍数与因数 师:我们只在非零自然数范围内研究倍数和因数。下面这两个算式中,你能说说,哪个数是哪个数的倍数,哪个数是哪个数的因数吗。 7×6=42 56÷7=8 师:你能用字母表示吗? 师:因数与倍数还有什么特征呢? 2.找一个数的倍数的方法 师:说说你是怎样找一个数的倍数的。 师:一个数的倍数有什么特征? 3.2,3,5的倍数特征 师:回忆一下,2,3,5的倍数都有什么特征? 4.找一个数的因数的方法 师:说说你是怎样找一个数的因数的。 师:怎样能不重不漏地找到呢? 5.一个数的倍数和因数的特点 师:一个数的倍数有什么特征?一个数的因数有什么特征? 6.非零自然数的分类 师:非零自然数可以怎样分类呢? 生1:这一单元我认识了倍数和因数,探索了2,3,5的倍数的特征。 生2:我还学会了找一个数因数的方法。 生3:我们还学习了质数与合数。 生1:6和7是42的因数,42是6和7的倍数。 生2:7和8是56的因数,56是7和8的倍数。 生1:如果a×b=c(a,b,c都是不为0的自然数),那么a和b就是c的因数,c是a和b的倍数。 生2:如果c÷a=b(a,b,c都是不为0的自然数),那么a和b就是c的因数,c是a和b的倍数。 生:倍数与因数是相互依存的关系,在说明倍数与因数时应该说明哪个数是哪个数的倍数,哪个数是哪个数的因数。 生1:可以用乘法算式找,也可以用除法算式找。 生2:写出一个数的倍数时,可以用乘法算式写,比如写出8在30以内的倍数。用8依次乘1,2,3,…,一直乘到积最接近但不大于30为止即可,8×1=8,8×2=16,8×3=24,8×4=32。所以8在30以内的倍数:8,16,24。 生3:判断一个数是否是另一个数的倍数时,可以用除法算式写,比如可以用除法算式判断136÷8=17,可知136是8的倍数;138÷8=17……2,可知138不是8的倍数。 生1:一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。 生1:2的倍数特征:个位上是2,4,6,8,0的数。 生2:5的倍数特征:个位上是0或5的数都是5的倍数。 生3:3的倍数特征:各个数位上数字之和是3的倍数。 生4:同时是2和5的倍数特征:个位上是0的数。 生5:同时是2和3的倍数特征:各个数位上数字之和是3的倍数的偶数。 生6:同时是3和5的倍数特征:各个数位上数字之和是3的倍数,且个位上是0或5。 生7:同时是2,3和5的倍数特征:各个数位上数字之和是3的倍数,且个位上是0。 生1:用乘法算式找,想哪两个数相乘是这个数。 生2:用除法算式找,想被除数是这个数的所有算式。 生:从1开始,一对一对找,按从小到大的顺序写。 生1:一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。 生2:一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。 生1:非零自然数按是不是2的倍数分:奇数、偶数。 生2:非零自然数按因数的个数分:1,质数,合数。 通过提问和举例的方式交流本单元重点内容。
环节二 综合练习 1.从下面的数中选出三个数,组成乘法或除法算式,再说说哪个数是哪个数的倍数,哪个数是哪个数的因数。 2.用24个小正方形摆长方形,有几种摆法?填一填,想一想,24的因数有哪些? 3.一个数既是6的倍数,又是24的因数,这个数可能是多少? 4.分一分,填一填,并与同伴交流你的想法。 5.分一分,填一填,并与同伴交流你的想法。 6.猜猜我是谁。 7.找出27的全部因数和100以内7的全部倍数。 27的全部因数: 。 100以内7的全部倍数: 。 8.选哪种包装盒能正好把90瓶饮料装完?还有其他的包装方式吗? 生1:2×6=12,12÷2=6。 2和6是12的因数,12是2和6的倍数。 生2:3×4=12,12÷3=4。 3和4是12的因数,12是3和4的倍数。 生3:2×12=24,24÷2=12。 2和12是24的因数,24是2和12的倍数。 生4:4×6=24,24÷4=6。 4和6是24的因数,24是4和6的倍数。 生:24=1×24=2×12=3×8=4×6。 有4种填法。 24的因数有1,2,3,4,6,8,12,24。 生:先列出6的倍数(24以内):6,12,18,24。 再列出24的所有因数:1,2,3,4,6,8,12,24。 这个数可能是6,12,24。 生: 生: 生1:比3大,比7小的奇数是5。 生2:两个数都是质数,和是15,这两个数是2和13。 生3:一个偶数,也是一个两位数,十位数字与个位数字的积是18,这个数是36或92。 生1:27的全部因数:1,3,9,27 生2:100以内7的全部倍数:7,14,21,28,35,42,49,56,63,70,77,84,91,98。 生1:每盒装6瓶,能正好整完。 生2:每盒装5瓶,能正好整完。 生3:每盒装3瓶,能正好整完。 生4:每盒装8瓶,不能正好整完。 其他的包装方式不唯一。 生1:每盒装9瓶,能装完。 生2:每盒装3瓶,装10盒,每盒装6瓶,装10盒。 …… 通过本单元典型题目的练习,巩固本单元重点。
环节三 拓展练习 1.已知A是质数,而且A+4,A+6,A+10都是质数,求符合条件的最小的质数是几? 2.小丽和小亮玩抽数字卡片游戏,有意思的是,一次两人抽出卡片上的数都是质数,且两个数的和是奇数,还是小于50的7的倍数。这两个质数的积可能是多少? 3.三个连续自然数的和都是3的倍数吗?三个连续奇数或偶数的和呢? 生:当A=2时,2+4=6,是合数,不合题意; 当A=3时,3+4=7,3+6=9,9是合数,不合题意; 当A=5时,5+4=9, 9是合数,不合题意; 当A=7时,7+4=11,7+6=13, 7+10=17,11,13,17都是质数,符合题意。 符合条件的最小的质数是7。 生:由两个数的和是奇数可知,一奇一偶。 由两个数都是质数是质数可知,其中一个数是2。 两个数的和是小于50的7的倍数:7,21,35,49。 另一个数:5,19,47。 两个质数的积可能是:2×5=10,2×19=38,2×47=94。 生: 设三个连续的自然数为n-1,n,n+1。 三个连续自然数的和: n-1+n+n+1=3n。 3n是3的倍数,所以三个连续自然数的和都是3的倍数。 设三个连续的偶数或奇数为n-2,n,n+2。 三个连续奇数或偶数的和: n-2+n+n+2=3n。 3n是3的倍数,所以三个连续奇数或偶数的和都是3的倍数。 在新的情境中,灵活运用本单元的知识解决问题。
环节四 课后活动 同学们,爸爸妈妈的手机号是多少,这些数字中有什么特征呢?请你描述出来,看谁猜的又快又准确! 布置一个小活动,学生从活动经验或感受中获得自己的经验。
2
第6课时 单元综合复习
教学内容分析:
本单元是在非零自然数范围内学习倍数与因数的相关知识,通过这部分知识的学习,一方面,使学生获得一些有关整数的知识;另一方面,有助于发展学生的抽象思维。在课堂上,教师与学生共同经历知识的整理过程,对所学知识进行罗列,对所罗列的知识进行归类,把同一类的知识放在一起,并利用适当的语言进行概括,再分析概括知识之间的前后联系。
教学目标:
1.回顾倍数与因数的相关内容,沟通知识之间的内在联系。
2.能正确运用因数、倍数的知识,并能解决一些实际问题。
3.通过回顾、整理、巩固应用等学习活动,养成整理知识、自我反思的良好习惯。
教学重点:
理解各个概念,分析各个概念之间的联系与区别。
教学难点:
应用所学知识解决实际问题。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 知识梳理 师:同学们,在这个单元中,我们都学习了哪些知识,请你翻翻数学书,一起来说一说。 师:下面我们就来一起回顾下,具体学习了什么。 1.倍数与因数 师:我们只在非零自然数范围内研究倍数和因数。下面这两个算式中,你能说说,哪个数是哪个数的倍数,哪个数是哪个数的因数吗。 7×6=42 56÷7=8 师:你能用字母表示吗? 师:因数与倍数还有什么特征呢? 2.找一个数的倍数的方法 师:说说你是怎样找一个数的倍数的。 师:一个数的倍数有什么特征? 3.2,3,5的倍数特征 师:回忆一下,2,3,5的倍数都有什么特征? 4.找一个数的因数的方法 师:说说你是怎样找一个数的因数的。 师:怎样能不重不漏地找到呢? 5.一个数的倍数和因数的特点 师:一个数的倍数有什么特征?一个数的因数有什么特征? 6.非零自然数的分类 师:非零自然数可以怎样分类呢? 生1:这一单元我认识了倍数和因数,探索了2,3,5的倍数的特征。 生2:我还学会了找一个数因数的方法。 生3:我们还学习了质数与合数。 生1:6和7是42的因数,42是6和7的倍数。 生2:7和8是56的因数,56是7和8的倍数。 生1:如果a×b=c(a,b,c都是不为0的自然数),那么a和b就是c的因数,c是a和b的倍数。 生2:如果c÷a=b(a,b,c都是不为0的自然数),那么a和b就是c的因数,c是a和b的倍数。 生:倍数与因数是相互依存的关系,在说明倍数与因数时应该说明哪个数是哪个数的倍数,哪个数是哪个数的因数。 生1:可以用乘法算式找,也可以用除法算式找。 生2:写出一个数的倍数时,可以用乘法算式写,比如写出8在30以内的倍数。用8依次乘1,2,3,…,一直乘到积最接近但不大于30为止即可,8×1=8,8×2=16,8×3=24,8×4=32。所以8在30以内的倍数:8,16,24。 生3:判断一个数是否是另一个数的倍数时,可以用除法算式写,比如可以用除法算式判断136÷8=17,可知136是8的倍数;138÷8=17……2,可知138不是8的倍数。 生1:一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。 生1:2的倍数特征:个位上是2,4,6,8,0的数。 生2:5的倍数特征:个位上是0或5的数都是5的倍数。 生3:3的倍数特征:各个数位上数字之和是3的倍数。 生4:同时是2和5的倍数特征:个位上是0的数。 生5:同时是2和3的倍数特征:各个数位上数字之和是3的倍数的偶数。 生6:同时是3和5的倍数特征:各个数位上数字之和是3的倍数,且个位上是0或5。 生7:同时是2,3和5的倍数特征:各个数位上数字之和是3的倍数,且个位上是0。 生1:用乘法算式找,想哪两个数相乘是这个数。 生2:用除法算式找,想被除数是这个数的所有算式。 生:从1开始,一对一对找,按从小到大的顺序写。 生1:一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。 生2:一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。 生1:非零自然数按是不是2的倍数分:奇数、偶数。 生2:非零自然数按因数的个数分:1,质数,合数。 通过提问和举例的方式交流本单元重点内容。
环节二 综合练习 1.从下面的数中选出三个数,组成乘法或除法算式,再说说哪个数是哪个数的倍数,哪个数是哪个数的因数。 2.用24个小正方形摆长方形,有几种摆法?填一填,想一想,24的因数有哪些? 3.一个数既是6的倍数,又是24的因数,这个数可能是多少? 4.分一分,填一填,并与同伴交流你的想法。 5.分一分,填一填,并与同伴交流你的想法。 6.猜猜我是谁。 7.找出27的全部因数和100以内7的全部倍数。 27的全部因数: 。 100以内7的全部倍数: 。 8.选哪种包装盒能正好把90瓶饮料装完?还有其他的包装方式吗? 生1:2×6=12,12÷2=6。 2和6是12的因数,12是2和6的倍数。 生2:3×4=12,12÷3=4。 3和4是12的因数,12是3和4的倍数。 生3:2×12=24,24÷2=12。 2和12是24的因数,24是2和12的倍数。 生4:4×6=24,24÷4=6。 4和6是24的因数,24是4和6的倍数。 生:24=1×24=2×12=3×8=4×6。 有4种填法。 24的因数有1,2,3,4,6,8,12,24。 生:先列出6的倍数(24以内):6,12,18,24。 再列出24的所有因数:1,2,3,4,6,8,12,24。 这个数可能是6,12,24。 生: 生: 生1:比3大,比7小的奇数是5。 生2:两个数都是质数,和是15,这两个数是2和13。 生3:一个偶数,也是一个两位数,十位数字与个位数字的积是18,这个数是36或92。 生1:27的全部因数:1,3,9,27 生2:100以内7的全部倍数:7,14,21,28,35,42,49,56,63,70,77,84,91,98。 生1:每盒装6瓶,能正好整完。 生2:每盒装5瓶,能正好整完。 生3:每盒装3瓶,能正好整完。 生4:每盒装8瓶,不能正好整完。 其他的包装方式不唯一。 生1:每盒装9瓶,能装完。 生2:每盒装3瓶,装10盒,每盒装6瓶,装10盒。 …… 通过本单元典型题目的练习,巩固本单元重点。
环节三 拓展练习 1.已知A是质数,而且A+4,A+6,A+10都是质数,求符合条件的最小的质数是几? 2.小丽和小亮玩抽数字卡片游戏,有意思的是,一次两人抽出卡片上的数都是质数,且两个数的和是奇数,还是小于50的7的倍数。这两个质数的积可能是多少? 3.三个连续自然数的和都是3的倍数吗?三个连续奇数或偶数的和呢? 生:当A=2时,2+4=6,是合数,不合题意; 当A=3时,3+4=7,3+6=9,9是合数,不合题意; 当A=5时,5+4=9, 9是合数,不合题意; 当A=7时,7+4=11,7+6=13, 7+10=17,11,13,17都是质数,符合题意。 符合条件的最小的质数是7。 生:由两个数的和是奇数可知,一奇一偶。 由两个数都是质数是质数可知,其中一个数是2。 两个数的和是小于50的7的倍数:7,21,35,49。 另一个数:5,19,47。 两个质数的积可能是:2×5=10,2×19=38,2×47=94。 生: 设三个连续的自然数为n-1,n,n+1。 三个连续自然数的和: n-1+n+n+1=3n。 3n是3的倍数,所以三个连续自然数的和都是3的倍数。 设三个连续的偶数或奇数为n-2,n,n+2。 三个连续奇数或偶数的和: n-2+n+n+2=3n。 3n是3的倍数,所以三个连续奇数或偶数的和都是3的倍数。 在新的情境中,灵活运用本单元的知识解决问题。
环节四 课后活动 同学们,爸爸妈妈的手机号是多少,这些数字中有什么特征呢?请你描述出来,看谁猜的又快又准确! 布置一个小活动,学生从活动经验或感受中获得自己的经验。
2
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
