第一单元第1课时《精打细算》表格式精品教案 数学北师大版 五年级上册
文档属性
| 名称 | 第一单元第1课时《精打细算》表格式精品教案 数学北师大版 五年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 531.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 17:24:49 | ||
图片预览



文档简介
第一单元 小数除法
第1课时 精打细算
教学内容分析:
本节课的内容是除数是整数的小数除法,主要研究“小数除以整数,除到被除数末尾无余数,商不补0”的各种情况。利用学生已有的知识经验,借助元、角、分之间的关系,探究除数是整数的小数除法的算理,并以此来解决除数是整数的小数除法的计算。并让学生结合问题解决的过程安排了三个问题。第一个问题借助元、角、分的生活经验和整数计算的知识基础,理解小数除法的计算过程;第二个问题借助元、角、分,理解小数除法竖式的计算过程;第三个问题进一步熟悉小数除法的计算过程及注意问题。
教学目标:
1.借助已有知识和生活经验,经历探索除数是整数的小数除法算法的过程,掌握小数除法的计算方法,发展推理能力。
2.能正确进行除数是整数的小数除法的竖式计算,并能解决一些简单的实际问题。
3.结合具体情境,体会小数除法在日常生活中的应用,进一步体会小数除法的意义。
教学重点:
引导学生理解和掌握小数除法的计算方法。
教学难点:
能正确进行除数是整数的小数除法的竖式计算,商的小数点要与被除数的小数点对齐。
教学过程:
教学环节 教师活动 学生活动 设计意图
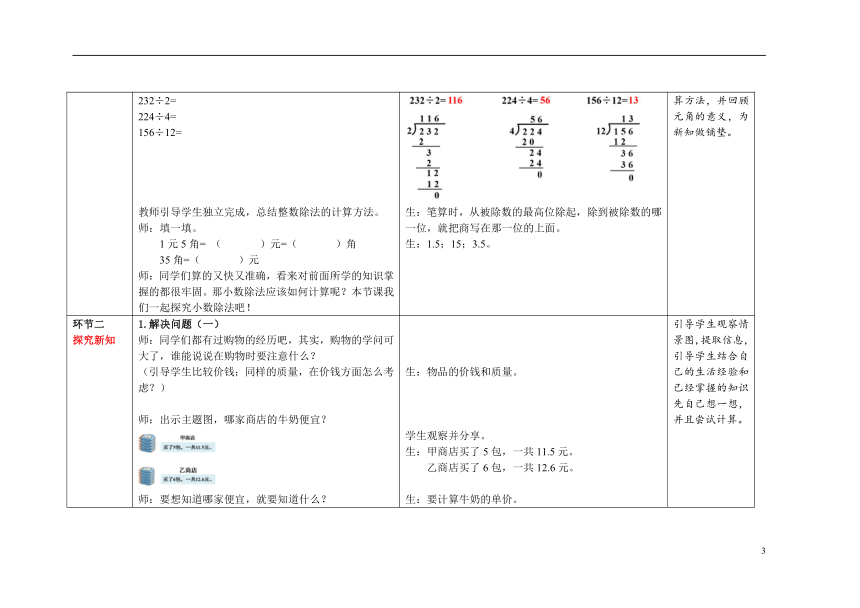
环节一 创设情境 【复习导入】 师:笔算下面各题,并说一说整数除法的计算方法。 课件出示: 232÷2= 224÷4= 156÷12= 教师引导学生独立完成,总结整数除法的计算方法。 师:填一填。 1元5角= ( )元=( )角 35角=( )元 师:同学们算的又快又准确,看来对前面所学的知识掌握的都很牢固。那小数除法应该如何计算呢?本节课我们一起探究小数除法吧! 学生独立完成。 生: 生:笔算时,从被除数的最高位除起,除到被除数的哪一位,就把商写在那一位的上面。 生:1.5;15;3.5。 通过复习导入,引导学生尝试总结整数除法的计算方法,并回顾元角的意义,为新知做铺垫。
环节二 探究新知 1.解决问题(一) 师:同学们都有过购物的经历吧,其实,购物的学问可大了,谁能说说在购物时要注意什么? (引导学生比较价钱;同样的质量,在价钱方面怎么考虑?) 师:出示主题图,哪家商店的牛奶便宜? 师:要想知道哪家便宜,就要知道什么? 师:甲商店每袋牛奶多少钱?应该如何列式呢? 师:还有不同的方法吗? 2.解决问题(二) 师:用竖式计算,说一说每一步的意思。 你是怎么从竖式中得到商的? 师小结: (1)用竖式计算; (2)都按照整数除法的方法来计算; (3)都研究了商的小数点为什么要和被除数的小数点对齐的问题。 3.解决问题(三) 师:甲商店牛奶的价格我们计算出来了,那么乙商店牛奶每袋多少元?哪家商店的牛奶便宜? 请同学们自由做题,允许同桌讨论,师巡视指导,并请做好的同学上黑板演示。 4.归纳总结 师:说一说除数是整数的小数除法的计算方法。 生:物品的价钱和质量。 学生观察并分享。 生:甲商店买了5包,一共11.5元。 乙商店买了6包,一共12.6元。 生:要计算牛奶的单价。 学生合作探究,交流反馈。 生:11.5元=115角 23角=2.3元 所以11.5÷5=2.3(元) 生:11.5元=10元+1.5元 10元÷5=2元 1.5元=15角 15角÷5=3角=0.3元 2元+0.3元=2.3元 所以 11.5÷5=2.3(元) 生1:用元、角解释。 生2:用小数的意义解释。 学生合作探究,分享成果。 生:12.6÷6=2.1(元) 2.1元<2.3元 答:乙商店的牛奶每袋2.1元,乙商店的牛奶更便宜。 生:除数是整数的小数除法: ①按整数除法的计算方法计算; ②商的小数点与被除数的小数点对齐。 引导学生观察情景图,提取信息,引导学生结合自己的生活经验和已经掌握的知识先自己想一想,并且尝试计算。 算法多样化,体现学生在已有的知识经验的基础上迁移出小数除法的计算方法,同时体会算理。培养学生的发散思维。 引导学生用竖式计算,并能够结合情景说出竖式中每一步的意思,加深对算理的理解。培养学生分析问题的能力和概括能力。 鼓励学生利用刚学的方法解决问题,培养学生独立解决问题的能力。
环节三 巩固新知 1. 星星文具店的钢笔每支多少元?阳光文具店的钢笔每支多少元? (2)说一说,哪个文具店的钢笔便宜?每支钢笔便宜多少元? 2.看一看,说一说竖式中每一步的意思。 这箱矿泉水一共28.8元,每瓶多少元? 3.列竖式计算。 9.6÷4= 25.2÷6= 34.5÷15= 学生独立完成,交流反馈。 生1:13.6÷2=6.8(元) 生2:19.5÷3=6.5(元) 答:星星文具店的钢笔每支6.8元,阳光文具店的钢笔每支6.5元。 生:6.8>6.5 6.8 6.5=0.3(元) 答:阳光文具店的钢笔更便宜,每支便宜0.3元。 生1:竖式中的“48”是4.8元,就是48角,表示48个0.1。 生2:商的小数部分的“2”是2角,表示2个0.1。 生3:商的小数点要与被除数的小数点对齐。 生: 一方面,利用小数除法的知识解决问题,指导学生在理解题意的基础上完整表述问题;另一方面,结合情境解释除数是整数的小数除法竖式的实际含义,加深对小数除法意义的理解。 结合具体情境,加深对除数是整数的小数除法竖式的理解。在交流时,关注学生对竖式中的余数部分、商的小数部分及小数点位置等方面的理解。 巩固竖式计算的方法。
环节四 课堂小结 你有什么收获? 生:知道了除数是整数的小数除法的计算方法。 ①按整数除法的计算方法计算。 ②商的小数点与被除数小数点对齐。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 拓展延伸 你知道小数的由来吗? 我国对小数的认识在世界上也是最早的。公元3世纪,我国数学家刘徽在注释《九章算术》中处理平方要根问题时就提出了十进小数。 虽然我国对小数的认识远远早于欧洲,但现代数学中所使用的小数的表示法却是从欧洲传入我国的。欧洲关于十进小数的最大贡献者是荷兰工程师斯蒂文。他从制造利息表中体会到十进小数的优越性,因此他竭力主张把十进小数引进到整个算术运算中去,使十进小数有效地参与记数。 不过,斯蒂文的小数记法并不高明,如139.654,他写作135⊙6①5②4③,每个数后面圈中的数是用来指明它前面数字位置的,这种表示方法,使小数的形式复杂化,并且给小数的运算带来很大的麻烦。1592年,瑞士数学家布尔基(Jobst Burgi)对此作出较大的改进。他用一空心小圆圈把整数部分和小数部分隔开,比如把36.548表示为36。548,这与现代的表示法已极为接近。 大约过了一年,德国的克拉维斯,首先用黑点代替了小圆圈。他在1608年发表的《代数学》中,将他的这一做法公之于世,至此,小数的现代记法才被确立下来。 数学小知识,增加学生的知识面和见闻,体会数学在生活中的应用。
环节六 布置作业 教材P3第3、4题
2
第1课时 精打细算
教学内容分析:
本节课的内容是除数是整数的小数除法,主要研究“小数除以整数,除到被除数末尾无余数,商不补0”的各种情况。利用学生已有的知识经验,借助元、角、分之间的关系,探究除数是整数的小数除法的算理,并以此来解决除数是整数的小数除法的计算。并让学生结合问题解决的过程安排了三个问题。第一个问题借助元、角、分的生活经验和整数计算的知识基础,理解小数除法的计算过程;第二个问题借助元、角、分,理解小数除法竖式的计算过程;第三个问题进一步熟悉小数除法的计算过程及注意问题。
教学目标:
1.借助已有知识和生活经验,经历探索除数是整数的小数除法算法的过程,掌握小数除法的计算方法,发展推理能力。
2.能正确进行除数是整数的小数除法的竖式计算,并能解决一些简单的实际问题。
3.结合具体情境,体会小数除法在日常生活中的应用,进一步体会小数除法的意义。
教学重点:
引导学生理解和掌握小数除法的计算方法。
教学难点:
能正确进行除数是整数的小数除法的竖式计算,商的小数点要与被除数的小数点对齐。
教学过程:
教学环节 教师活动 学生活动 设计意图
环节一 创设情境 【复习导入】 师:笔算下面各题,并说一说整数除法的计算方法。 课件出示: 232÷2= 224÷4= 156÷12= 教师引导学生独立完成,总结整数除法的计算方法。 师:填一填。 1元5角= ( )元=( )角 35角=( )元 师:同学们算的又快又准确,看来对前面所学的知识掌握的都很牢固。那小数除法应该如何计算呢?本节课我们一起探究小数除法吧! 学生独立完成。 生: 生:笔算时,从被除数的最高位除起,除到被除数的哪一位,就把商写在那一位的上面。 生:1.5;15;3.5。 通过复习导入,引导学生尝试总结整数除法的计算方法,并回顾元角的意义,为新知做铺垫。
环节二 探究新知 1.解决问题(一) 师:同学们都有过购物的经历吧,其实,购物的学问可大了,谁能说说在购物时要注意什么? (引导学生比较价钱;同样的质量,在价钱方面怎么考虑?) 师:出示主题图,哪家商店的牛奶便宜? 师:要想知道哪家便宜,就要知道什么? 师:甲商店每袋牛奶多少钱?应该如何列式呢? 师:还有不同的方法吗? 2.解决问题(二) 师:用竖式计算,说一说每一步的意思。 你是怎么从竖式中得到商的? 师小结: (1)用竖式计算; (2)都按照整数除法的方法来计算; (3)都研究了商的小数点为什么要和被除数的小数点对齐的问题。 3.解决问题(三) 师:甲商店牛奶的价格我们计算出来了,那么乙商店牛奶每袋多少元?哪家商店的牛奶便宜? 请同学们自由做题,允许同桌讨论,师巡视指导,并请做好的同学上黑板演示。 4.归纳总结 师:说一说除数是整数的小数除法的计算方法。 生:物品的价钱和质量。 学生观察并分享。 生:甲商店买了5包,一共11.5元。 乙商店买了6包,一共12.6元。 生:要计算牛奶的单价。 学生合作探究,交流反馈。 生:11.5元=115角 23角=2.3元 所以11.5÷5=2.3(元) 生:11.5元=10元+1.5元 10元÷5=2元 1.5元=15角 15角÷5=3角=0.3元 2元+0.3元=2.3元 所以 11.5÷5=2.3(元) 生1:用元、角解释。 生2:用小数的意义解释。 学生合作探究,分享成果。 生:12.6÷6=2.1(元) 2.1元<2.3元 答:乙商店的牛奶每袋2.1元,乙商店的牛奶更便宜。 生:除数是整数的小数除法: ①按整数除法的计算方法计算; ②商的小数点与被除数的小数点对齐。 引导学生观察情景图,提取信息,引导学生结合自己的生活经验和已经掌握的知识先自己想一想,并且尝试计算。 算法多样化,体现学生在已有的知识经验的基础上迁移出小数除法的计算方法,同时体会算理。培养学生的发散思维。 引导学生用竖式计算,并能够结合情景说出竖式中每一步的意思,加深对算理的理解。培养学生分析问题的能力和概括能力。 鼓励学生利用刚学的方法解决问题,培养学生独立解决问题的能力。
环节三 巩固新知 1. 星星文具店的钢笔每支多少元?阳光文具店的钢笔每支多少元? (2)说一说,哪个文具店的钢笔便宜?每支钢笔便宜多少元? 2.看一看,说一说竖式中每一步的意思。 这箱矿泉水一共28.8元,每瓶多少元? 3.列竖式计算。 9.6÷4= 25.2÷6= 34.5÷15= 学生独立完成,交流反馈。 生1:13.6÷2=6.8(元) 生2:19.5÷3=6.5(元) 答:星星文具店的钢笔每支6.8元,阳光文具店的钢笔每支6.5元。 生:6.8>6.5 6.8 6.5=0.3(元) 答:阳光文具店的钢笔更便宜,每支便宜0.3元。 生1:竖式中的“48”是4.8元,就是48角,表示48个0.1。 生2:商的小数部分的“2”是2角,表示2个0.1。 生3:商的小数点要与被除数的小数点对齐。 生: 一方面,利用小数除法的知识解决问题,指导学生在理解题意的基础上完整表述问题;另一方面,结合情境解释除数是整数的小数除法竖式的实际含义,加深对小数除法意义的理解。 结合具体情境,加深对除数是整数的小数除法竖式的理解。在交流时,关注学生对竖式中的余数部分、商的小数部分及小数点位置等方面的理解。 巩固竖式计算的方法。
环节四 课堂小结 你有什么收获? 生:知道了除数是整数的小数除法的计算方法。 ①按整数除法的计算方法计算。 ②商的小数点与被除数小数点对齐。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 拓展延伸 你知道小数的由来吗? 我国对小数的认识在世界上也是最早的。公元3世纪,我国数学家刘徽在注释《九章算术》中处理平方要根问题时就提出了十进小数。 虽然我国对小数的认识远远早于欧洲,但现代数学中所使用的小数的表示法却是从欧洲传入我国的。欧洲关于十进小数的最大贡献者是荷兰工程师斯蒂文。他从制造利息表中体会到十进小数的优越性,因此他竭力主张把十进小数引进到整个算术运算中去,使十进小数有效地参与记数。 不过,斯蒂文的小数记法并不高明,如139.654,他写作135⊙6①5②4③,每个数后面圈中的数是用来指明它前面数字位置的,这种表示方法,使小数的形式复杂化,并且给小数的运算带来很大的麻烦。1592年,瑞士数学家布尔基(Jobst Burgi)对此作出较大的改进。他用一空心小圆圈把整数部分和小数部分隔开,比如把36.548表示为36。548,这与现代的表示法已极为接近。 大约过了一年,德国的克拉维斯,首先用黑点代替了小圆圈。他在1608年发表的《代数学》中,将他的这一做法公之于世,至此,小数的现代记法才被确立下来。 数学小知识,增加学生的知识面和见闻,体会数学在生活中的应用。
环节六 布置作业 教材P3第3、4题
2
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
