1.2 有理数同步练习题(含答案)
文档属性
| 名称 | 1.2 有理数同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1007.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 22:12:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.2有理数人教版数学七年级上册
一、选择题(共10题,共20分)
(2分)a 是最小的正整数,b 是最大的负整数,c 是绝对值最小的有理数,则 a,b,c 三数之和是( )
A. 1 B.0 C.1 D.2
(2分)在数 1,0, 1, 2 中,最小的数是( )
A. 1 B. 0 C. 1 D. 2
(2分)下列各数中,属于有理数的是( )
A. 67 B. 36 C. π
D. 3.1313313331 (两个“1”之间依次多一个 3)
(2分) 3 的相反数是 ( )
A.3 B. 3 C.13 D. 13
(2分)在 2, 2,8,6 这四个数中,互为相反数的是( )
A. 2 与 2 B.2 与 8 C. 2 与 6 D.6 与 8
(2分)在数轴上,原点及原点左侧的点表示的数是( )
A.整数 B.非正数 C.非负数 D.负数
(2分)下列说法中正确的是 ( )
A.任何有理数的绝对值都是正数
B.最大的负有理数是 1
C.0 是最小的数
D.如果两个数互为相反数,那么它们的绝对值相等
(2分)如图,若 A 是有理数 a 在数轴上对应的点,则关于 a, a,1 的大小关系表示正确的是( )
A. a<1< a B. a< a<1 C. 1< a(2分)关于① 227 与② 22 的说法正确的是( )
A.①②都是有理数 B.①是无理数,②是有理数
C.①是有理数,②是无理数 D.①②都是无理数
(2分)若 a= 3.5,则 a=( )
A. 3.5 B. 3.5 C. ±3.5 D.以上都不对
二、填空题(共9题,共20分)
(2分)计算:∣ 3∣= .
(2分)如图,在数轴上点 A,B 表示的数分别是 1, 2,若点 B,C 到点 A 的距离相等,则点 C 所表示的数是 .
(2分)数轴上点 M 表示有理数 2,将点 M 向右平移 1 个单位长度到达点 N,点 E 到点 N 的距离为 4,则点 E 表示的有理数为 .
(4分)在数轴上到 3 的距离为 5 的数是 ,在数轴上到 3 和 2 的距离之和为 10 的数是 .
(2分)在数 3, 2,0,3 中,大小在 1 和 2 之间的数是 .
(2分) m,n 是有理数,它们在数轴上的对应点的位置如图所示,化简 ∣n m∣ 的结果是 .
(2分)绝对值小于 4.5 的非负整数有 .
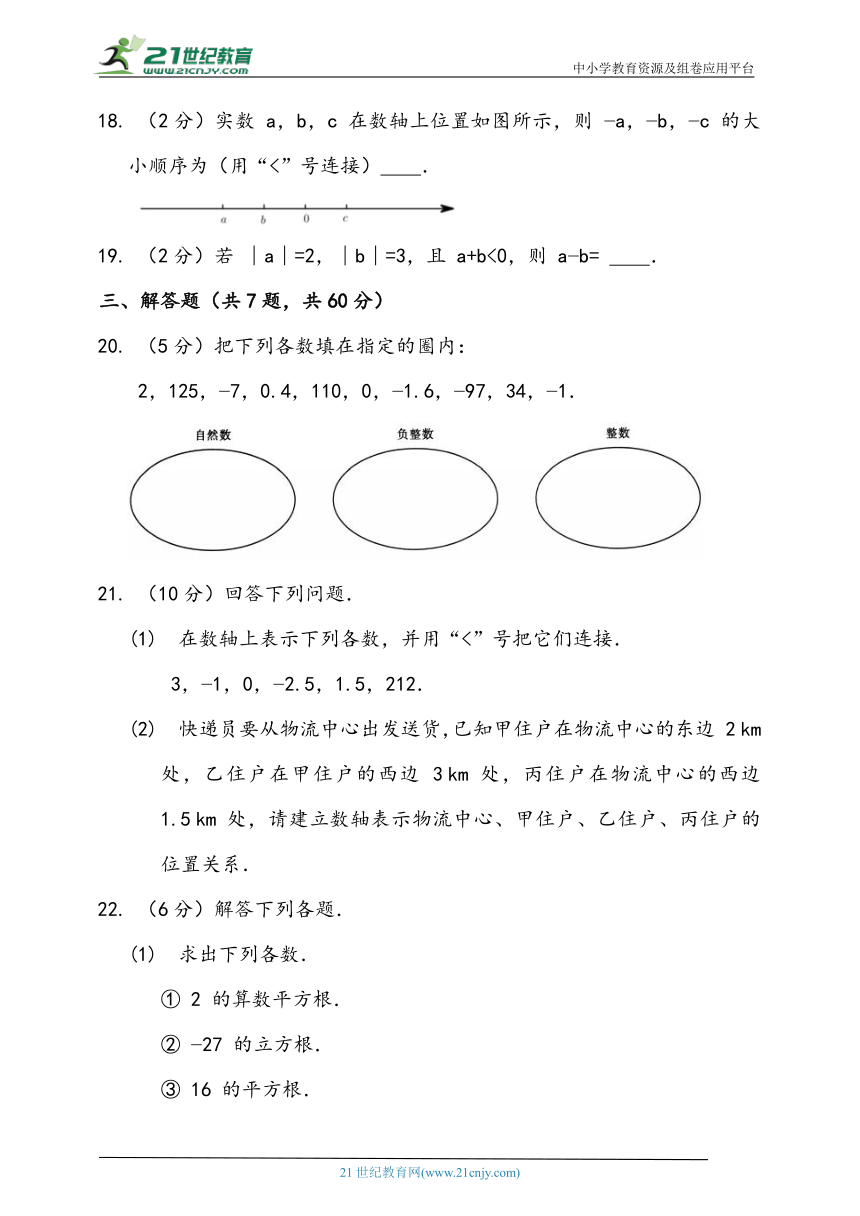
(2分)实数 a,b,c 在数轴上位置如图所示,则 a, b, c 的大小顺序为(用“<”号连接) .
(2分)若 ∣a∣=2,∣b∣=3,且 a+b<0,则 a b= .
三、解答题(共7题,共60分)
(5分)把下列各数填在指定的圈内:
2,125, 7,0.4,110,0, 1.6, 97,34, 1.
(10分)回答下列问题.
(1) 在数轴上表示下列各数,并用“<”号把它们连接.
3, 1,0, 2.5,1.5,212.
(2) 快递员要从物流中心出发送货,已知甲住户在物流中心的东边 2 km 处,乙住户在甲住户的西边 3 km 处,丙住户在物流中心的西边 1.5 km 处,请建立数轴表示物流中心、甲住户、乙住户、丙住户的位置关系.
(6分)解答下列各题.
(1) 求出下列各数.
① 2 的算数平方根.
② 27 的立方根.
③ 16 的平方根.
(2) 将(1)中求出的每个数准确地表示在数轴上,将这些数按从小到大的顺序排列,并用“<”连接.
(7分)有理数 a,b 在数轴上对应点如图所示:
在数轴上表示出 a, b;
(2) 试把 a,b,0, a, b 这 5 个数从小到大用”<”连接起来.
(8分)观察下列每对数在数轴上对应点间的距离:4 与 2,3 与 5, 2 与 6, 4 与 3.如:4 与 2 对应点间的距离是 ∣4 2∣=6;3 与 5 对应点间的距离是 ∣3 5∣=2.回答下列问题:
若数轴上 A,B 两点分别表示有理数 a,b,则 A,B 两点间的距离是多少?(用含 a,b 的式子表示)
(2) 若数轴上的点 A 表示的数为 x,点 B 表示的数为 1,则 A 与 B 两点间的距离可以表示为 .
(3) 结合数轴可得 ∣x 2∣+∣x+3∣ 的最小值为 ;
(4) 若关于 x 的方程 ∣x 1∣+∣x+1∣+∣x 5∣=a 无解,则 a 的取值范围是 .
(10分) A,B,C,D 四个车站的位置如图所示,A,B 两站之间的距离 AB=a b,B,C 两站之间的距离 BC=2a b,B,D 两站之间的距离 BD=72a 2b 1.求:
(1) A,C 两站之间的距离 AC;
(2) 若 A,C 两站之间的距离 AC=180 km,求 C,D 两站之间的距离 CD.
(14分)对于有理数 a,b,定义一种新运算“⊙”,规定 a⊙b=∣a+b∣+∣a b∣.
(1) 计算 2⊙ 3 的值.
(2) 当 a,b 在数轴上的位置如图所示时,化简 a⊙b.
(3) 当 a⊙b=a⊙c 时,是否一定有 b=c 或者 b= c?若是,则说明理由;若不是,则举例说明.
(4) 已知 a⊙a⊙a=8+a,求 a 的值.
答案
一、选择题(共10题,共20分)
1. 【答案】B
2. 【答案】D
3. 【答案】A
4. 【答案】A
5. 【答案】A
6. 【答案】B
7. 【答案】D
8. 【答案】A
9. 【答案】C
10. 【答案】C
二、填空题(共9题,共20分)
11. 【答案】 3
12. 【答案】 2+2
13. 【答案】 3 或 5
14. 【答案】 8或2; 5.5或4.5
15. 【答案】 0
16. 【答案】 m n
17. 【答案】 0,1,2,3,4
18. 【答案】 c= b< a
19. 【答案】 1 或 5
三、解答题(共7题,共60分)
20. 【答案】自然数:2,125,0
负整数: 7, 97, 1
整数:2,125, 7,0, 97, 1
21. 【答案】
(1) 由数轴可知,左边的数小于右边的数,则 2.5< 1<0<1.5<212<3.
(2) 以物流中心为原点,正方向为东,单位长度为 1 km,
则甲所在位置为 +2 km,乙所在位置为 +2 3= 1 km,
丙所在位置为 0 1.5= 1.5 km.
如图所示.
22. 【答案】
(1) ① 2 的算数平方根是 2.
② 27 的立方根是 3.
③ 16=4,±4=±2,
∴16 的平方根是 ±2.
(2) 把题(1)中求出的数表示在数轴上如下:
∴ 3< 2<2<2.
23. 【答案】
(1) a, b 表示图略:
(2) 由上面数轴可知, a24. 【答案】
(1) 由观察可知:A,B 两点间的距离是 ∣b a∣(或 ∣a b∣).
(2) ∣x+1∣
(3) 5
(4) a<6
25. 【答案】
(1) A,C 两站之间的距离 AC=a b+2a b=3a 2b.
(2) CD=72a 2b 1 2a b=32a b 1,
∵3a 2b=180 km,
∴32a b=90 km,
∴CD=90 1=89km.
答:C,D 两站之间的距离 CD 是 89 km.
26. 【答案】
(1) 根据题中的新定义得:2⊙ 3=∣2+ 3∣+∣2 3∣=1+5=6.
(2) 从 a,b 在数轴上的位置可得 a+b<0,a b>0,
∴a⊙b=∣a+b∣+∣a b∣= a+b+a b= 2b.
(3) 由 a⊙b=a⊙c 得:∣a+b∣+∣a b∣=∣a+c∣+∣a c∣,不一定有 b=c 或者 b= c,例如:取 a=5,b=4,c=3,则 ∣a+b∣+∣a b∣=∣a+c∣+∣a c∣=10,此时等式成立,但 b≠c 且 b≠ c.
(4) 当 a≥0 时,a⊙a⊙a=2a⊙a=4a=8+a,解得:a=83;
当 a<0 时,a⊙a⊙a= 2a⊙a= 4a=8+a,解得:a= 85.
故 a 的值为:83 或 85.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.2有理数人教版数学七年级上册
一、选择题(共10题,共20分)
(2分)a 是最小的正整数,b 是最大的负整数,c 是绝对值最小的有理数,则 a,b,c 三数之和是( )
A. 1 B.0 C.1 D.2
(2分)在数 1,0, 1, 2 中,最小的数是( )
A. 1 B. 0 C. 1 D. 2
(2分)下列各数中,属于有理数的是( )
A. 67 B. 36 C. π
D. 3.1313313331 (两个“1”之间依次多一个 3)
(2分) 3 的相反数是 ( )
A.3 B. 3 C.13 D. 13
(2分)在 2, 2,8,6 这四个数中,互为相反数的是( )
A. 2 与 2 B.2 与 8 C. 2 与 6 D.6 与 8
(2分)在数轴上,原点及原点左侧的点表示的数是( )
A.整数 B.非正数 C.非负数 D.负数
(2分)下列说法中正确的是 ( )
A.任何有理数的绝对值都是正数
B.最大的负有理数是 1
C.0 是最小的数
D.如果两个数互为相反数,那么它们的绝对值相等
(2分)如图,若 A 是有理数 a 在数轴上对应的点,则关于 a, a,1 的大小关系表示正确的是( )
A. a<1< a B. a< a<1 C. 1< a(2分)关于① 227 与② 22 的说法正确的是( )
A.①②都是有理数 B.①是无理数,②是有理数
C.①是有理数,②是无理数 D.①②都是无理数
(2分)若 a= 3.5,则 a=( )
A. 3.5 B. 3.5 C. ±3.5 D.以上都不对
二、填空题(共9题,共20分)
(2分)计算:∣ 3∣= .
(2分)如图,在数轴上点 A,B 表示的数分别是 1, 2,若点 B,C 到点 A 的距离相等,则点 C 所表示的数是 .
(2分)数轴上点 M 表示有理数 2,将点 M 向右平移 1 个单位长度到达点 N,点 E 到点 N 的距离为 4,则点 E 表示的有理数为 .
(4分)在数轴上到 3 的距离为 5 的数是 ,在数轴上到 3 和 2 的距离之和为 10 的数是 .
(2分)在数 3, 2,0,3 中,大小在 1 和 2 之间的数是 .
(2分) m,n 是有理数,它们在数轴上的对应点的位置如图所示,化简 ∣n m∣ 的结果是 .
(2分)绝对值小于 4.5 的非负整数有 .
(2分)实数 a,b,c 在数轴上位置如图所示,则 a, b, c 的大小顺序为(用“<”号连接) .
(2分)若 ∣a∣=2,∣b∣=3,且 a+b<0,则 a b= .
三、解答题(共7题,共60分)
(5分)把下列各数填在指定的圈内:
2,125, 7,0.4,110,0, 1.6, 97,34, 1.
(10分)回答下列问题.
(1) 在数轴上表示下列各数,并用“<”号把它们连接.
3, 1,0, 2.5,1.5,212.
(2) 快递员要从物流中心出发送货,已知甲住户在物流中心的东边 2 km 处,乙住户在甲住户的西边 3 km 处,丙住户在物流中心的西边 1.5 km 处,请建立数轴表示物流中心、甲住户、乙住户、丙住户的位置关系.
(6分)解答下列各题.
(1) 求出下列各数.
① 2 的算数平方根.
② 27 的立方根.
③ 16 的平方根.
(2) 将(1)中求出的每个数准确地表示在数轴上,将这些数按从小到大的顺序排列,并用“<”连接.
(7分)有理数 a,b 在数轴上对应点如图所示:
在数轴上表示出 a, b;
(2) 试把 a,b,0, a, b 这 5 个数从小到大用”<”连接起来.
(8分)观察下列每对数在数轴上对应点间的距离:4 与 2,3 与 5, 2 与 6, 4 与 3.如:4 与 2 对应点间的距离是 ∣4 2∣=6;3 与 5 对应点间的距离是 ∣3 5∣=2.回答下列问题:
若数轴上 A,B 两点分别表示有理数 a,b,则 A,B 两点间的距离是多少?(用含 a,b 的式子表示)
(2) 若数轴上的点 A 表示的数为 x,点 B 表示的数为 1,则 A 与 B 两点间的距离可以表示为 .
(3) 结合数轴可得 ∣x 2∣+∣x+3∣ 的最小值为 ;
(4) 若关于 x 的方程 ∣x 1∣+∣x+1∣+∣x 5∣=a 无解,则 a 的取值范围是 .
(10分) A,B,C,D 四个车站的位置如图所示,A,B 两站之间的距离 AB=a b,B,C 两站之间的距离 BC=2a b,B,D 两站之间的距离 BD=72a 2b 1.求:
(1) A,C 两站之间的距离 AC;
(2) 若 A,C 两站之间的距离 AC=180 km,求 C,D 两站之间的距离 CD.
(14分)对于有理数 a,b,定义一种新运算“⊙”,规定 a⊙b=∣a+b∣+∣a b∣.
(1) 计算 2⊙ 3 的值.
(2) 当 a,b 在数轴上的位置如图所示时,化简 a⊙b.
(3) 当 a⊙b=a⊙c 时,是否一定有 b=c 或者 b= c?若是,则说明理由;若不是,则举例说明.
(4) 已知 a⊙a⊙a=8+a,求 a 的值.
答案
一、选择题(共10题,共20分)
1. 【答案】B
2. 【答案】D
3. 【答案】A
4. 【答案】A
5. 【答案】A
6. 【答案】B
7. 【答案】D
8. 【答案】A
9. 【答案】C
10. 【答案】C
二、填空题(共9题,共20分)
11. 【答案】 3
12. 【答案】 2+2
13. 【答案】 3 或 5
14. 【答案】 8或2; 5.5或4.5
15. 【答案】 0
16. 【答案】 m n
17. 【答案】 0,1,2,3,4
18. 【答案】 c= b< a
19. 【答案】 1 或 5
三、解答题(共7题,共60分)
20. 【答案】自然数:2,125,0
负整数: 7, 97, 1
整数:2,125, 7,0, 97, 1
21. 【答案】
(1) 由数轴可知,左边的数小于右边的数,则 2.5< 1<0<1.5<212<3.
(2) 以物流中心为原点,正方向为东,单位长度为 1 km,
则甲所在位置为 +2 km,乙所在位置为 +2 3= 1 km,
丙所在位置为 0 1.5= 1.5 km.
如图所示.
22. 【答案】
(1) ① 2 的算数平方根是 2.
② 27 的立方根是 3.
③ 16=4,±4=±2,
∴16 的平方根是 ±2.
(2) 把题(1)中求出的数表示在数轴上如下:
∴ 3< 2<2<2.
23. 【答案】
(1) a, b 表示图略:
(2) 由上面数轴可知, a
(1) 由观察可知:A,B 两点间的距离是 ∣b a∣(或 ∣a b∣).
(2) ∣x+1∣
(3) 5
(4) a<6
25. 【答案】
(1) A,C 两站之间的距离 AC=a b+2a b=3a 2b.
(2) CD=72a 2b 1 2a b=32a b 1,
∵3a 2b=180 km,
∴32a b=90 km,
∴CD=90 1=89km.
答:C,D 两站之间的距离 CD 是 89 km.
26. 【答案】
(1) 根据题中的新定义得:2⊙ 3=∣2+ 3∣+∣2 3∣=1+5=6.
(2) 从 a,b 在数轴上的位置可得 a+b<0,a b>0,
∴a⊙b=∣a+b∣+∣a b∣= a+b+a b= 2b.
(3) 由 a⊙b=a⊙c 得:∣a+b∣+∣a b∣=∣a+c∣+∣a c∣,不一定有 b=c 或者 b= c,例如:取 a=5,b=4,c=3,则 ∣a+b∣+∣a b∣=∣a+c∣+∣a c∣=10,此时等式成立,但 b≠c 且 b≠ c.
(4) 当 a≥0 时,a⊙a⊙a=2a⊙a=4a=8+a,解得:a=83;
当 a<0 时,a⊙a⊙a= 2a⊙a= 4a=8+a,解得:a= 85.
故 a 的值为:83 或 85.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
