面积的计算[上学期]

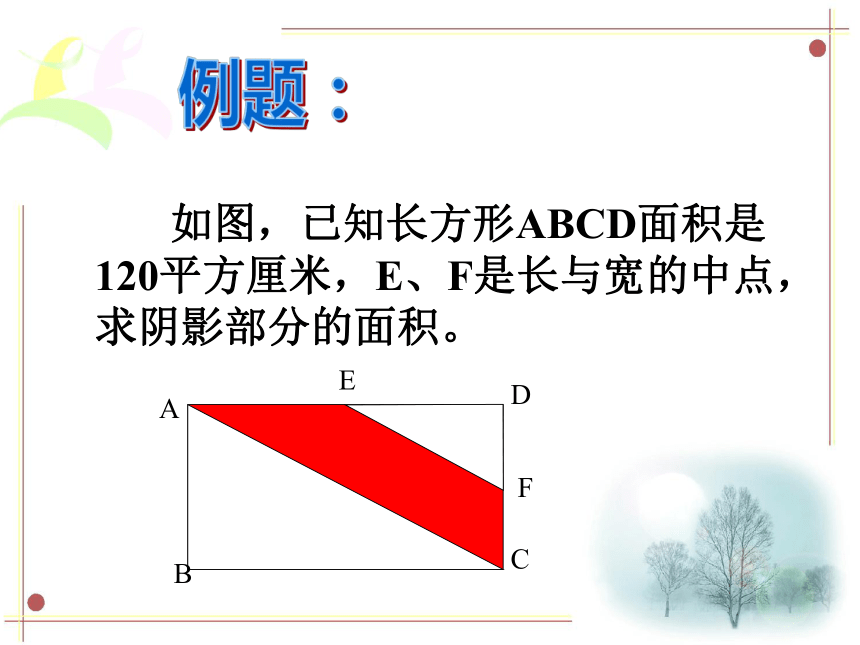
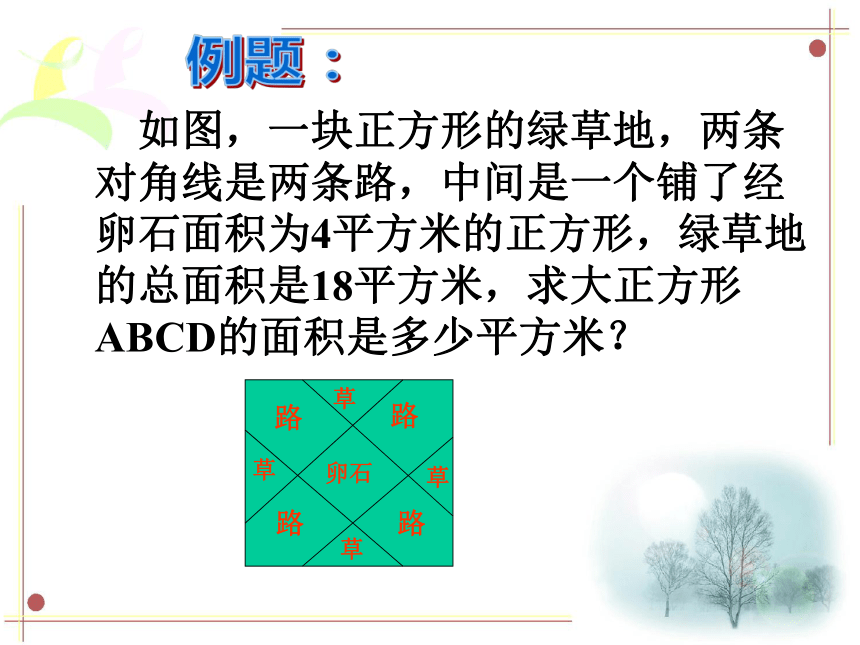
课件14张PPT。面积的计算（1）“割补法”方法和技巧（2）“分解法”（3）运用平移、旋转等方法对图形进行变形来求解例题： 如图的梯形中，两个阴影部分的面积之和是多少平方分米？（单位：分米）例题： 一块长方形铁皮，在长边截下6厘米，短边截下3厘米后得到一个正方形，如右图，面积比原长方形面积少了54平方厘米，求原长方形铁皮的面积。例题： 如图，已知长方形ABCD面积是120平方厘米，E、F是长与宽的中点，求阴影部分的面积。例题： 如图，一块正方形的绿草地，两条对角线是两条路，中间是一个铺了经卵石面积为4平方米的正方形，绿草地的总面积是18平方米，求大正方形ABCD的面积是多少平方米？习题： 如图的梯形中，你能否用两种方法求两个阴影部分的面积之和？（单位：分米）习题： 一块长方形纸片，在长边剪去5厘米，短边剪去2厘米后如图得到的正方形面积比原长方形面积少31平方厘米。求原长方形纸片的面积。习题： 如图，A、B两点分别是长方形的长和宽的中点，C、E、F分别为长方形的顶点，求阴影部分占长方形面积的几分之几？习题：求图中阴影部分（绿）的面积。（单位：厘米）3333555588 有两个房间，其中一间房里有三盏灯，另一间房里有控制这三盏灯的开关。这两间房是相对独立、相对封闭的，没有空间上的直接联系；三盏灯与三个开关也没有顺序上的必然联系。现在只允许你分别进入这两个房间一次，然后判断三盏灯分别是由哪个开关控制的。试一试：想一想 有一列火车以每小时140千米的速度离开洛杉矶直奔纽约，同时，另一列火车以每小时160千米的速度从纽约开往洛杉矶。如果有一只鸟以每小时30千米的速度和两列火车同时启动，从洛杉矶出发，碰到另一列车后返回，往返在两列火车间，直到两列火车相遇为止。已知洛杉矶到纽约的铁路长4500千米，请问，这只小鸟飞行了多远的路程？ 有7克、2克砝码各一个，天平一架，如何只用这些物品三次将140克的盐分成50克、90克各一份？比一比关键：用2克、7克称5克盐作为砝码