数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共40张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.2空间向量基本定理 课件(共40张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 751.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 14:18:07 | ||
图片预览










文档简介
(共40张PPT)
第一章《空间向量与立体几何》人教A版2019选择性必修第一册1.2空间向量基本定理环节一:创设情境,引入课题
我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.这三个空间向量是不共面的
如何用这三个向量表示空间中任意的向量呢?
我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
问题1:空间中怎样的向量能构成基底?
空间任意三个“不共面”的向量都可以作为空间向量的一个基底.
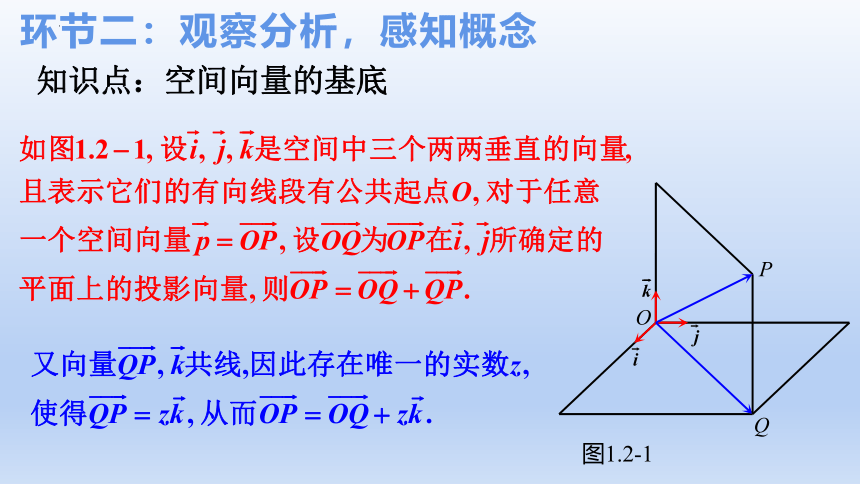
环节二:观察分析,感知概念
知识点:空间向量的基底
O
P
Q
图1.2-1
问题2:基底与基向量的概念有什么不同?
一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念;
空间任意三个不共面的向量都可构成空间的一个基底.
基底选定后,空间的所有向量均可由基底唯一表示;
不同基底下,同一向量的表达式也有可能不同.
问题3:空间的基底唯一吗?
不唯一,只要是三个向量不共面,这三个向量就可以组成空间的一个基底.
类似平面向量基本定理,我们有空间向量基本定理.
请你自己给出空间向量基本定理的证明.
O
P
Q
问题4:为什么空间向量基本定理中x,y,z是唯一的?
你能证明唯一性吗
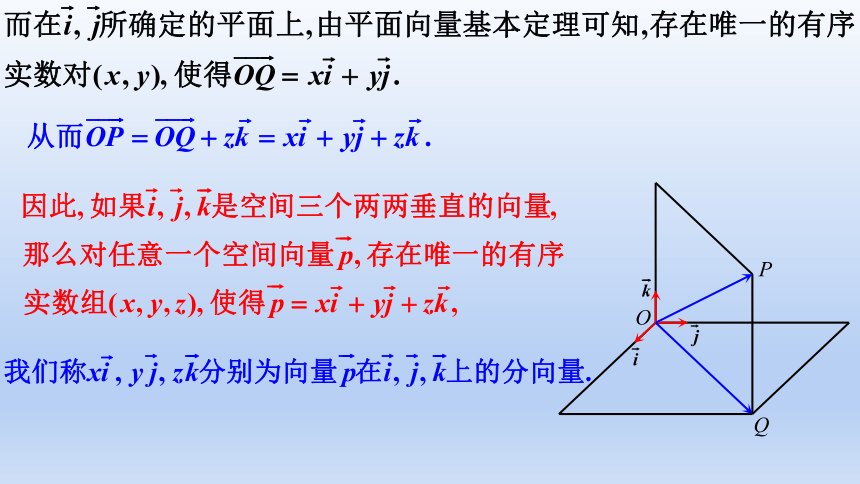
环节三:抽象概括,形成概念
环节四:辨析理解,深化概念
由空间向量基本定理可知,如果把三个不共面的向量作为空间的一个基底,那么所有空间向量都可以用三个基向量表示出来.
进一步地,所有空间向量间的运算都可以转化为基向量间的运算,这为解决问题带来了方便.
A
B
C
M
N
P
O
环节五:课堂练习,巩固运用
A
B
C
M
N
P
O
图1.2-2
练习(第12页)
A
B
C
O
G
(第3题)
A
B
C
O
G
(第3题)
A
B
C
D
M
N
B1
A1
C1
D1
图1.2-3
A
B
C
D
M
N
B1
A1
C1
D1
图1.2-3
A
B
C
D
E
F
G
图1.2-4
A
B
C
D
E
F
G
图1.2-4
A
B
C
D
E
F
G
图1.2-4
环节六:归纳总结,反思提升
用基底表示向量的三个步骤
(1)定基底:根据已知条件,确定三个不共面的向量构成空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结合相等向量的代换、向量的运算进行变形、化简,最后求出结果.
(3)下结论:利用空间向量的一个基底{a,b,c}可以表示出空间所有向量.表示要彻底、结果中只能含有a,b,c,不能含有其他形式的向量.
环节七:目标检测,作业布置
1.知识总结:通过这节课,你学到了什么知识?
2.学生反思:在解决问题时,用到了哪些数学思想?
A
B
C
O
练习(第14页)
A
B
C
D
A
B
C
O
D
(第3题)
A
B
C
O
D
(第3题)
习题1.2(第15页)
C
O
A
B
C
M
N
A
B
C
M
N
A
B
C
D
B1
A1
C1
D1
M
A
B
C
D
B1
A1
C1
D1
A
B
C
D
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
S
A
B
C
E
F
M
N
G
H
8.已知四面体中三组相对棱的中点间的距离都相等,
求证:这个四面体相对的棱两两垂直.
S
A
B
C
E
F
M
N
G
H
8.已知四面体中三组相对棱的中点间的距离都相等,求证:这个四面体相对的棱两两垂直.
第一章《空间向量与立体几何》人教A版2019选择性必修第一册1.2空间向量基本定理环节一:创设情境,引入课题
我们所在的教室即是一个三维立体图,如果以教室的一个墙角为始点,沿着三条墙缝作向量可以得到三个空间向量.这三个空间向量是不共面的
如何用这三个向量表示空间中任意的向量呢?
我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
问题1:空间中怎样的向量能构成基底?
空间任意三个“不共面”的向量都可以作为空间向量的一个基底.
环节二:观察分析,感知概念
知识点:空间向量的基底
O
P
Q
图1.2-1
问题2:基底与基向量的概念有什么不同?
一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念;
空间任意三个不共面的向量都可构成空间的一个基底.
基底选定后,空间的所有向量均可由基底唯一表示;
不同基底下,同一向量的表达式也有可能不同.
问题3:空间的基底唯一吗?
不唯一,只要是三个向量不共面,这三个向量就可以组成空间的一个基底.
类似平面向量基本定理,我们有空间向量基本定理.
请你自己给出空间向量基本定理的证明.
O
P
Q
问题4:为什么空间向量基本定理中x,y,z是唯一的?
你能证明唯一性吗
环节三:抽象概括,形成概念
环节四:辨析理解,深化概念
由空间向量基本定理可知,如果把三个不共面的向量作为空间的一个基底,那么所有空间向量都可以用三个基向量表示出来.
进一步地,所有空间向量间的运算都可以转化为基向量间的运算,这为解决问题带来了方便.
A
B
C
M
N
P
O
环节五:课堂练习,巩固运用
A
B
C
M
N
P
O
图1.2-2
练习(第12页)
A
B
C
O
G
(第3题)
A
B
C
O
G
(第3题)
A
B
C
D
M
N
B1
A1
C1
D1
图1.2-3
A
B
C
D
M
N
B1
A1
C1
D1
图1.2-3
A
B
C
D
E
F
G
图1.2-4
A
B
C
D
E
F
G
图1.2-4
A
B
C
D
E
F
G
图1.2-4
环节六:归纳总结,反思提升
用基底表示向量的三个步骤
(1)定基底:根据已知条件,确定三个不共面的向量构成空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结合相等向量的代换、向量的运算进行变形、化简,最后求出结果.
(3)下结论:利用空间向量的一个基底{a,b,c}可以表示出空间所有向量.表示要彻底、结果中只能含有a,b,c,不能含有其他形式的向量.
环节七:目标检测,作业布置
1.知识总结:通过这节课,你学到了什么知识?
2.学生反思:在解决问题时,用到了哪些数学思想?
A
B
C
O
练习(第14页)
A
B
C
D
A
B
C
O
D
(第3题)
A
B
C
O
D
(第3题)
习题1.2(第15页)
C
O
A
B
C
M
N
A
B
C
M
N
A
B
C
D
B1
A1
C1
D1
M
A
B
C
D
B1
A1
C1
D1
A
B
C
D
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
A
B
C
D
F
G
E
B1
A1
C1
D1
S
A
B
C
E
F
M
N
G
H
8.已知四面体中三组相对棱的中点间的距离都相等,
求证:这个四面体相对的棱两两垂直.
S
A
B
C
E
F
M
N
G
H
8.已知四面体中三组相对棱的中点间的距离都相等,求证:这个四面体相对的棱两两垂直.
