第14章等腰三角形的复习[上学期]
文档属性
| 名称 | 第14章等腰三角形的复习[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-14 00:00:00 | ||
图片预览



文档简介
课件13张PPT。等 腰 三 角 形复习课湖北荆门外语学校 陈贤富1.什么叫等腰三角形?答:有两边相等的三角形叫做等腰三角形。2.等腰三角形有哪些性质?(1)等腰三角形的两个底角( )。一、概念回顾(2)等腰三角形( )平分线, ( )上的中线, ( )上的高相互重合。(3)等腰三角形是轴对称图形,对称轴是( )。 3 . 等腰三角形,等边三角形的判定方法: (1)有两个角相等的三角形是( )三角形。(2)有三个角都相等的三角形是( )三角形。(3)有一个角等于60o的等腰三角形是( )三角形。 ACD 1、已知等腰△ABC,AB=AC,∠A = 36o ,BD是
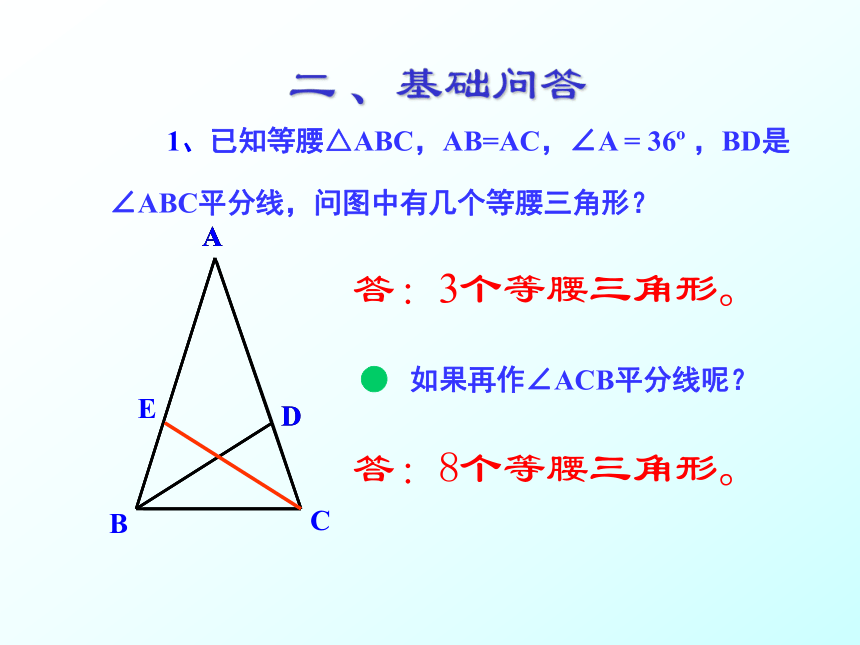
∠ABC平分线,问图中有几个等腰三角形?
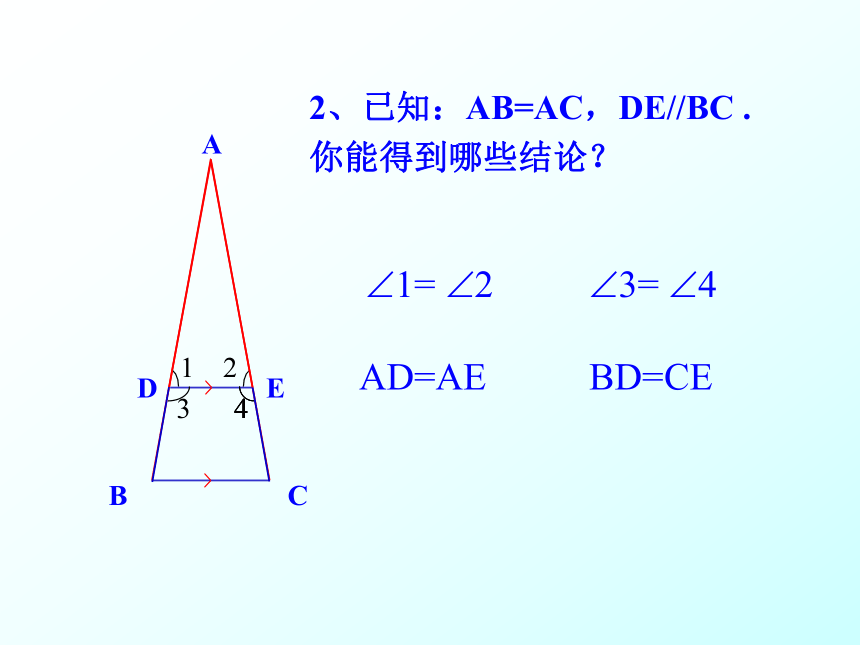
A答:3个等腰三角形。● 如果再作∠ACB平分线呢?答:8个等腰三角形。ADBAE二 、基础问答2、已知:AB=AC,DE//BC .
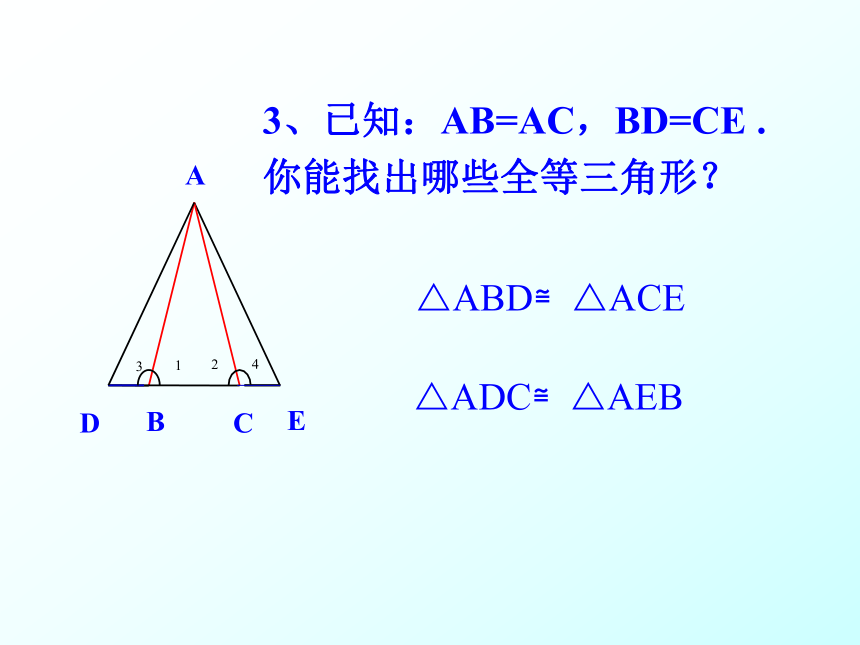
你能得到哪些结论? ?1= ?2 AD=AE ?3= ?4 BD=CE3、已知:AB=AC,BD=CE .
你能找出哪些全等三角形? ?ABD≌?ACE?ADC≌?AEB4、已知:AB=AC,BD平分?ABC , CE平分?ACB
你能得到哪些三角形全等??ABD ≌?ACE?BCE ≌?CBD?BOE ≌?CODABCEDOF5、已知:AB=AC,OB=OC,
能得到几对全等三角形?可以得到七对全等三角形:
?ABD ≌?ACE
?BCE ≌?CBD
?BOE ≌?COD
?AEO ≌?ADO
?ABO ≌?ACO
?BOF ≌?COF
?ABF ≌?ACFABCEFG证明:∵EG ∥BD∴ EF=FC( )同理:FG=FC∴ EF=FG123∴ ∠1=∠3( )又∵ ∠1=∠2∴ ∠2=∠3D分析: 能否直接证明 EF = GF? 若不能,应把哪条线段作桥梁沟通?三、例题选讲ABCD 12 EF由 ∠1=∠2想到:延长BE交AD的延长线于F容 易证AB=AF DF=BC即可于是只须证明∟例 2 已知:如图, ∠1 = ∠2 , AE⊥BE ,E 是 DC 的中点 求证:AB = AD + BC 分析: =AD+DF证明:(请大家自己完成)思考题:已知△ABC为等边三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,直线BN与AM相交于点Q.(1)先用量角器测量∠BQM的大小,然后猜测∠BQM等于多少度. (2)作BP垂直QM于P,猜想BQ于QP的大小关系,证明你的结论。四、课堂练习1.等腰三角形两边长分别是4cm和9cm,则周长为2. △ABC中, ∠A的外角平分线AE ∥BC,则△ABC是 三角形22cm等腰3.如图,△ABC中,AD平分∠BAC交BC于点D,
DE ∥AC,若DE=5cm,则AE=5cmACEBD5. 如图,AB=AC, ∠A=40°,AB的垂直平
分线MN交AC于点D,则∠DBC=30°4.如图,△ABC中, AB=AC, D在BC上,且
AD=BD,AC=CD,则∠ABC=36°ABDCABCMND 通过本节复习同学们应该掌握:
1、对等腰三角形有关概念、性质、判定的熟练应用。
2、学会从不同的角度分析问题、探究问题,解决问题,寻求最佳途径。五 课堂小结复习题14 A层 P156 4,5,6,12
B、C层 P156 4,6,12,14作业:你的进步是我最大的心愿!
∠ABC平分线,问图中有几个等腰三角形?
A答:3个等腰三角形。● 如果再作∠ACB平分线呢?答:8个等腰三角形。ADBAE二 、基础问答2、已知:AB=AC,DE//BC .
你能得到哪些结论? ?1= ?2 AD=AE ?3= ?4 BD=CE3、已知:AB=AC,BD=CE .
你能找出哪些全等三角形? ?ABD≌?ACE?ADC≌?AEB4、已知:AB=AC,BD平分?ABC , CE平分?ACB
你能得到哪些三角形全等??ABD ≌?ACE?BCE ≌?CBD?BOE ≌?CODABCEDOF5、已知:AB=AC,OB=OC,
能得到几对全等三角形?可以得到七对全等三角形:
?ABD ≌?ACE
?BCE ≌?CBD
?BOE ≌?COD
?AEO ≌?ADO
?ABO ≌?ACO
?BOF ≌?COF
?ABF ≌?ACFABCEFG证明:∵EG ∥BD∴ EF=FC( )同理:FG=FC∴ EF=FG123∴ ∠1=∠3( )又∵ ∠1=∠2∴ ∠2=∠3D分析: 能否直接证明 EF = GF? 若不能,应把哪条线段作桥梁沟通?三、例题选讲ABCD 12 EF由 ∠1=∠2想到:延长BE交AD的延长线于F容 易证AB=AF DF=BC即可于是只须证明∟例 2 已知:如图, ∠1 = ∠2 , AE⊥BE ,E 是 DC 的中点 求证:AB = AD + BC 分析: =AD+DF证明:(请大家自己完成)思考题:已知△ABC为等边三角形,点M是射线BC上任意一点,点N是射线CA上任意一点,且BM=CN,直线BN与AM相交于点Q.(1)先用量角器测量∠BQM的大小,然后猜测∠BQM等于多少度. (2)作BP垂直QM于P,猜想BQ于QP的大小关系,证明你的结论。四、课堂练习1.等腰三角形两边长分别是4cm和9cm,则周长为2. △ABC中, ∠A的外角平分线AE ∥BC,则△ABC是 三角形22cm等腰3.如图,△ABC中,AD平分∠BAC交BC于点D,
DE ∥AC,若DE=5cm,则AE=5cmACEBD5. 如图,AB=AC, ∠A=40°,AB的垂直平
分线MN交AC于点D,则∠DBC=30°4.如图,△ABC中, AB=AC, D在BC上,且
AD=BD,AC=CD,则∠ABC=36°ABDCABCMND 通过本节复习同学们应该掌握:
1、对等腰三角形有关概念、性质、判定的熟练应用。
2、学会从不同的角度分析问题、探究问题,解决问题,寻求最佳途径。五 课堂小结复习题14 A层 P156 4,5,6,12
B、C层 P156 4,6,12,14作业:你的进步是我最大的心愿!
