2023浙教版科学七升八暑期“快人一步”培优讲义(四):浮力(3)--沉浮综合【word,含答案】
文档属性
| 名称 | 2023浙教版科学七升八暑期“快人一步”培优讲义(四):浮力(3)--沉浮综合【word,含答案】 |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-07-05 15:21:39 | ||
图片预览



文档简介
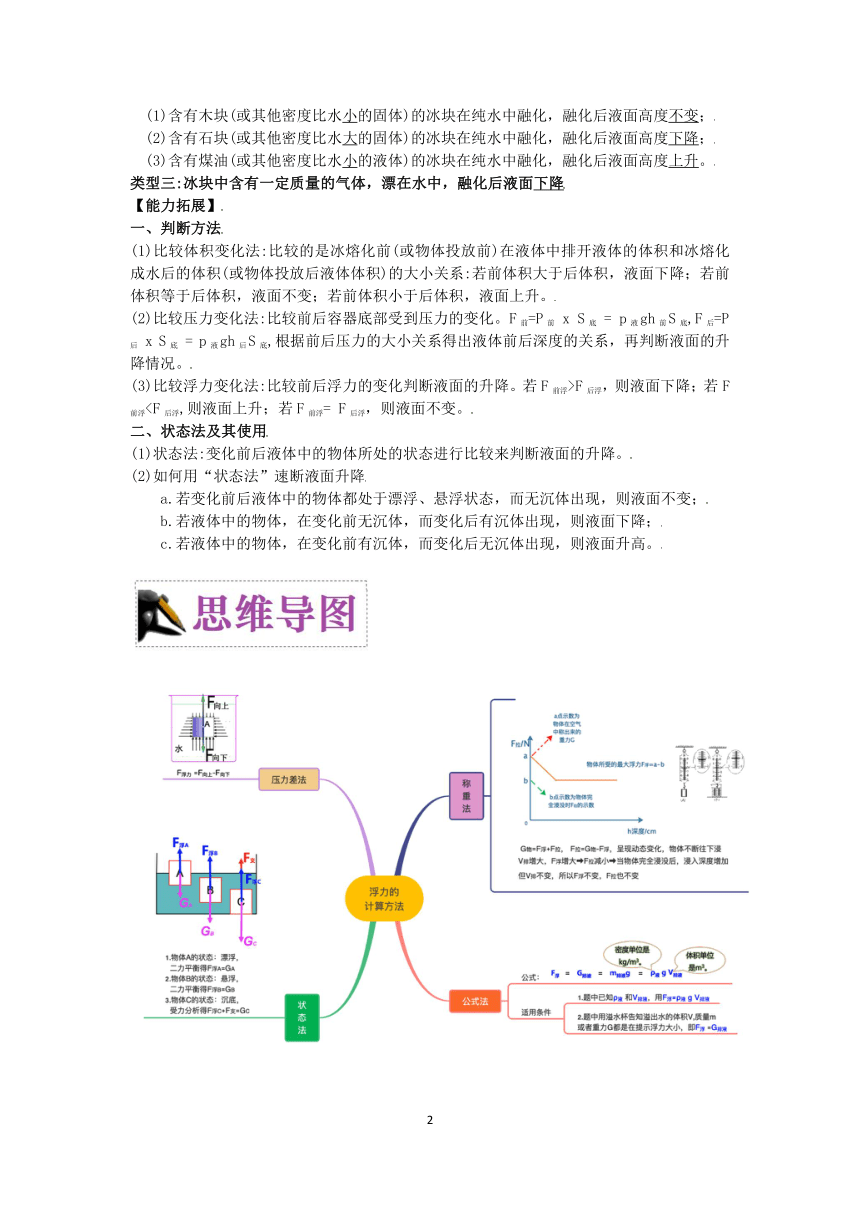
一、浮力的计算
1.原则:对于复杂情况,我们一般先进行受力分析,然后再代入公式计算。
2.压力差法:F=F-F。
3.阿基米德原理公式:F=G=ρgV
4.平衡法:F=G,该公式只有在物体悬浮、漂浮于液体表面的时候才成立。
5.受力分析:F=G-F,物体在浮力、重力、向下的压力下处于平衡态,那么浮力公式就是:F=G+F。
二、绳子、弹簧等受力分析
物体在液体中处于稳定状态,通常会受到重力、浮力、拉力(弹力)、支持力等作用,先利用二力平衡的条件受力分析,进一步答题。
【能力拓展】
浮力计算基本步骤
①确定研究对象
②确定物体运动状态
③确定物体受力情况
④确定计算方法
三、 液面高度变化问题
类型一:冰漂在某液体
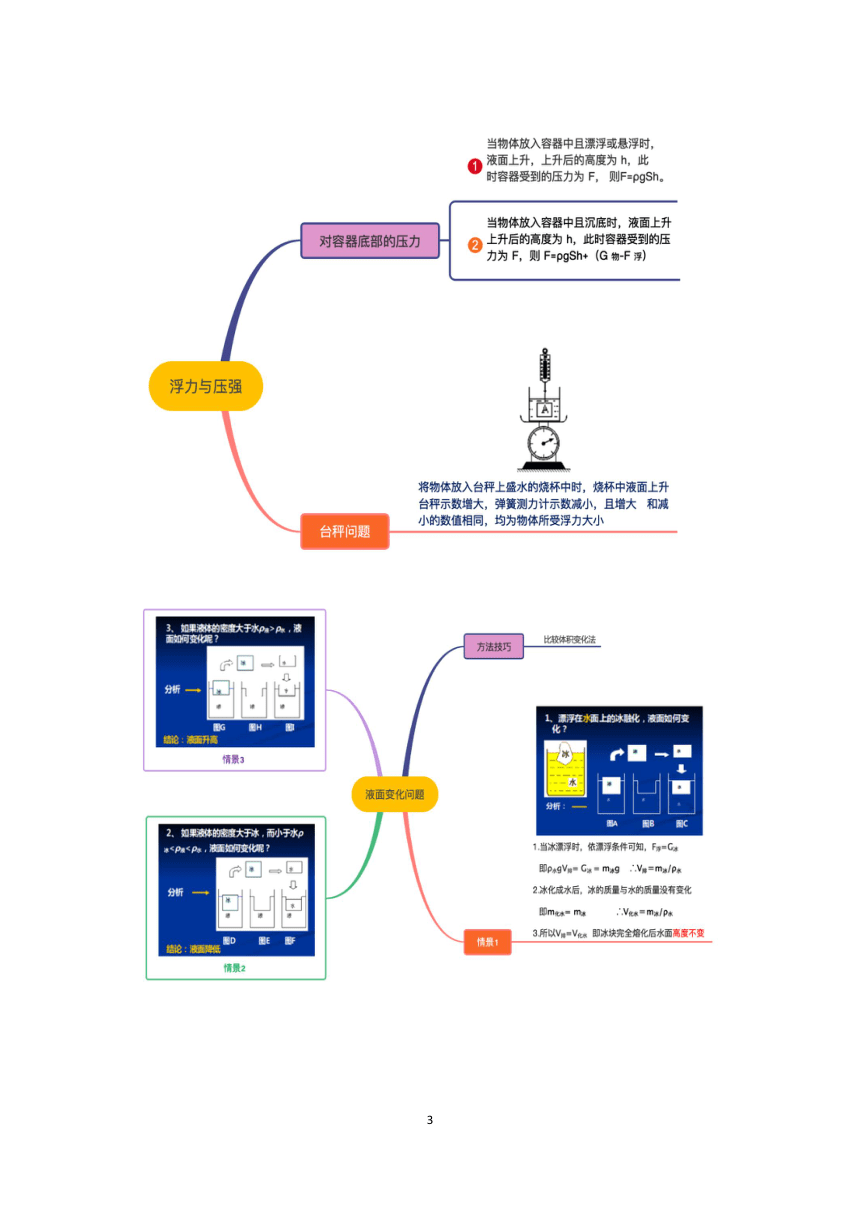
(1)纯冰在纯水中融化,融化后液面高度不变;
(2)纯冰在盐水(或其他密度比水大的液体)中融化,融化后液面升高;
(3)纯冰在密度比水小的液体中融化,融化后液面高度降低。
类型二:冰块中含有其他杂质,漂在水中
(1)含有木块(或其他密度比水小的固体)的冰块在纯水中融化,融化后液面高度不变;
(2)含有石块(或其他密度比水大的固体)的冰块在纯水中融化,融化后液面高度下降;
(3)含有煤油(或其他密度比水小的液体)的冰块在纯水中融化,融化后液面高度上升。
类型三:冰块中含有一定质量的气体,漂在水中,融化后液面下降
【能力拓展】
一、判断方法
(1)比较体积变化法:比较的是冰熔化前(或物体投放前)在液体中排开液体的体积和冰熔化成水后的体积(或物体投放后液体体积)的大小关系:若前体积大于后体积,液面下降;若前体积等于后体积,液面不变;若前体积小于后体积,液面上升。
(2)比较压力变化法:比较前后容器底部受到压力的变化。F前=P前 x S底 = p液gh前S底,F后=P后 x S底 = p液gh后S底,根据前后压力的大小关系得出液体前后深度的关系,再判断液面的升降情况。
(3)比较浮力变化法:比较前后浮力的变化判断液面的升降。若F前浮>F后浮,则液面下降;若F前浮二、状态法及其使用
(1)状态法:变化前后液体中的物体所处的状态进行比较来判断液面的升降。
(2)如何用“状态法”速断液面升降
a.若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;
b.若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;
c.若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高。
例1、如图所示,某圆柱形薄壁容器装有适量的水,其底面积为20cm2 , 将物体B放入水中时,通过台秤测得总质量150g;使用一绳子提起物体B,物体B刚好有一半体积露出水面时保持静止不动,此时台秤示数为70g,并测得容器内液面下降了1cm。则物体B的密度是( )
A.1.5×103kg/m3 B.2.0×103kg/m3 C.2.5×103kg/m3 D.3.0×103kg/m3
例2、如图所示,在一个装满水的容器中,轻质弹簧的一端连着小球,另一端固定在容器底部。已知小球的体积是500cm3,小球静止时受到弹簧对它的作用力为4N。则:
(1)此时小球受到的浮力为多少?
(2)如果剪断弹簧后,请分析小球的运动情况,并计算再次静止后小球受到的浮力是多少?
例3、如图甲所示为一个浮力感应装置,竖直细杆的上端通过力传感器连在天花板上,传感器可以显示出细杆的上端受到作用力的大小,下端与物体M相连,水箱的质量为0.8kg,细杆及连接处的重力可忽略不计,向图甲所示的空水箱中加水直到刚好加满,图乙是力传感器的示数大小随水箱中加入水质量变化的图像:求:
(1)物体M受到的重力?
(2)物体M被浸没时,受到的浮力多少N?
(3)当向容器中加水2.1kg时,传感器的示数为F0,F0大小为多少牛?
(4)当传感器示数变为3F0时,水箱对地面的压力为多少牛?
1.如图所示,在一块浮在水面的长方体木块上放一质量为272克的铁块甲,木块恰好浸没在水中。拿掉铁块甲,用细线把铁块乙系在木块下面,木块也恰好浸没在水中,则铁块乙的质量为( )(ρ铁=7.8克/厘米3 , ρ水=1.0克/厘米3)
A.312克 B.237克 C.318克 D.326克
2.学了浮力知识后,小刚同学想探究冰在不同液体中熔化后的液面升降情况,他用如图的方法,把冰块分别放入浓盐水、酒精,水中,结果熔化后液面比原来下降的是( )
A.盐水 B.酒精 C.水 D.无法判断
3.如图,四个相同的容器内水面一样高,a容器内有水,b容器内有木块漂浮在水面上,c容器内漂浮着一块冰块,d容器中悬浮着一个空心球。下列四种说法正确的一组是()
①每个容器的总质量都相等;②四个容器中,液体对容器底的压强相同;③在 b 容器中倒入酒精后,木块在液面下的体积减小;④c 容器中冰块融化后水面高度将下降;⑤d 容器中倒入酒精后,小球将下沉。
A.①②④ B.①③⑤ C.①②⑤ D.②③④
4.如图为底部有一小孔的花盆倒扣在水槽中,小明发现塑料花盆缓慢下沉直至沉入水槽 底部,这个过程中花盆受到的浮力和水槽中液面的高度变化正确的是( )
A.浮力变大,液面高度下降 B.浮力变小,液面高度下降
C.浮力变大,液面高度上升 D.浮力变小,液面高度上升
5.如图所示,两只完全相同的容器分别装等质量的水放在台秤上,用细线悬挂着质量相同的实心铅球和铝球,逐渐将它们全部浸没在水中(球未接触到容器底,水未溢出),此时台秤甲、乙示数分别为N1和N2 , 绳的拉力分别为T1和T2 , 已知ρ铅>ρ铝 , 则下列关系正确的是( )
A.N1=N2 T1>T2 B.N1>N2 T1>T2 C.N1<N2 T1>T2 D.N1>N2 T1<T2
6.小金把家里景观水池底部的鹅卵石取出清洗他先将一个重为10N的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面(不考虑捞出过程中带出的水,ρ水=1.0×103kg/m3)
(1)空桶漂浮在水面时所受浮力大小
(2)鹅卵石捞出放置在桶内时,水池水面高度与鹅卵石未捞出时相比会 (选填“上升”、“下降”或“不变”)。若此时桶排开水的体积为6.0×10-3m3 , 求桶内鹅卵石的质量。
7.一边长为10cm,密度为0.6g/cm3的正方体木块,用细线置于容器的水中,此时木块下表面到水面的距离为15cm,如图所示,求:
(1)木块上表面处的压强大小;
(2)细线的拉力大小;
(3)细线剪断后,木块静止时,木块所受的浮力大小?
1.如下图所示,四个相同的容器内水面一样高,a容器内只有水,b容器内有木块漂浮在水面上,c容器内漂浮着一块冰块,d容器中悬浮着一个空心球。则下列四种说法正确的一组是( )
① 每个容器的总质量都相等
② b容器中再倒入酒精后,木块在液面下的体积减小
③ c容器中冰块熔化后水面高度升高
④ d容器中再倒入酒精后,小球将下沉
A.③④ B.①④ C.①② D.②④
2.如图所示水平地面上有底面积为,质量不计的薄壁柱形盛水容器A,内有质量为,边长为,质量分布均匀的正方体物块B,通过一根的细线与容器底部相连,此时水面距容器底,剪断绳子后,木块最终静止时有的体积露出水面,计算可得出( )
A.剪断绳子前,水对容器底部的压力为
B.剪断绳子前,容器对水平地面的压力是
C.剪断绳子,待物块静止后漂浮在水面上,水平地面受到的压强变化了
D.剪断绳子,待物块静止后漂浮在水面上,水对容器底的压强变化了
3.如图,一个弹簧一端固定物体,另一端固定在容器底部,放在装满水的装置中处于静止.设想从某一天起,地球的引力减为一半,则弹簧对物体的弹力(弹簧处于压缩状态)( )
A.不变 B.减为一半
C.增加为原值两倍 D.弹簧对物体无弹力
4.如图所示,将重为 8 N 的物块用细绳拴在装有某液体的容器底部,已知容器底部的面积为 100 cm2,物块的体积为 1 dm3。剪断细绳,电子秤的示数变化了 0.5 kg。求:
(1)剪断细绳前,物块所受的浮力 (选填“小于”“等于”或“大于”)物块的重力。
(2)剪断细绳后,液体对容器底部的压强变化了 。
(3)液体的密度为 。
5.如图所示,用细线系着体积为600cm3、密度为0.6g/cm3的长方体木块,静置于水中(水的密度为1.0×103kg/m3)。求:
(1)木块所受的F浮大小。
(2)细线对木块的拉力F大小。
(3)若木块上下底的面积均为100cm2,剪断细线后,求木块最终静止时,其底部所受水的压强大小(木块最终静止时上下底面与水面平行)。
答案及解析
例1、C
【解析】台秤的示数等于上面物体的总重力,据此列出两种情况下台秤示数与重力的等量关系式,然后通过推导得到B的体积和质量,最后根据密度公式计算即可。
【解答】第一次通过磅秤测得总质量150g,
那么上面的总重力G=mg=0.15kg×10N/kg; 即G杯+G水+GB=1.5N…①
第二次此时磅秤示数为70g;
那么上面的总重力G'=m'g=0.07×10N/kg=0.7N;
设全部浸入时浮力为F浮 , 这里一半体积浸入,故此时的浮力为 ,
则G杯+G水+F浮=0.7N…②
由①-②得,GB- F浮=0.8N…③,
由“物体B刚好有一半体积露出水面时保持静止不动,测得容器内液面下降了1cm。”
可得: ; 解得:V=4×10-5m3;
原来受到的浮力: F浮=ρ水gV排=1.0×103kg/m3×10N/kg×4×10-5m3=0.4N;
将F浮=0.4N代入③, 解得:GB=1N;
则B的质量为:;
物体B的密度。
例2、(1)物体浸没时, V排=V物,利用阿基米德原理公式 F浮=ρ液g V排求出 此时小球受到的浮力;(2) 小球静止时对其进行受力分析可分为二种情况:一种情况是 小球下沉至容器底部静止,求出浮力;另一种情况是小球上浮至水面处于飘浮状态。
例3、(1)2N;(2)10N;(3)1.5N;(4)47.5N
【解析】
【详解】
解:(1)由图乙可知,水箱中没有水时(m=0),压力传感器受到的拉力F1=2N,则物体M的重力
G=F1=2N
(2)由图乙可知,当M完全浸没时,压力传感器的示数为
F2=8N>2N
细杆对传感器的作用力为压力,故传感器对细杆有向下的作用力
F=F2=8N
作用于物体M:此时物体M受到竖直向上的浮力、竖直向下的重力和杆的作用力,处于静止状态,则M受到的浮力
F浮=G+F=2N+8N=10N
(3)综上可知,加水2kg时水面达到M的下表面(此时浮力为0),加水4kg时M刚好浸没(此时浮力为10N),该过程中增加水的质量为2kg,浮力增大了10N,所以,每加1kg水,物体M受到的浮力增加5N;当向水箱中加入质量为2.1kg的水时,受到的浮力
则此时杆的作用力为拉力,力传感器的示数
F0=G-F浮1=2N-0.5N=1.5N
(4)继续向水箱中加水,当力传感器的示数大小变为3F0时,即
F3=3F0=3×1.5N=4.5N>2N
由此可知,此时杆的作用力为压力,物体M受到的浮力
F浮2=G+F3=2N+4.5N=6.5N
此时容器内水的质量
m水2=2kg+6.5N×1kg/5N=3.3kg
把水箱和水、物体M看做整体,受力分析可知,受到竖直向下的总重力和杆向下的压力3F0、水平面的支持力作用处于平衡状态,由整体受到的合力为零可得
F支持=(m水2+m水箱)g+G+F3=(3.3kg+0.8kg)×10N/kg+2N+4.5N=47.5N
此时水箱对水平面的压力
F压=F支持=47.5N
答:(1)物体M受到的重力为2N;
(2)物体M被浸没时,受到的浮力为10N;
(3)当向容器中加水2.1kg时,传感器的示数为F0,F0大小为1.5N;
(4)当传感器示数变为3F0时,水箱对地面的压力为47.5N。
1.A
【解析】由甲图可知木块和甲铁块漂浮,由乙图可知木块和乙铁块悬浮,根据物体的浮沉条件和阿基米德原理得出等式,即可求出乙铁块的体积,再根据m=ρV求出铁块乙的质量。
【解答】木块和甲铁块在水面漂浮,
那么F浮甲=G甲+G木;
即ρ水gV木=m甲g+G木 ①;
木块和乙铁块在水中悬浮, 那么F浮乙=G乙+G木;
即ρ水g(V木+V乙)=ρ铁gV乙+G木 ②;
②-①得到:ρ水gV乙=ρ铁gV乙-m甲g;
ρ水V乙=ρ铁V乙-m甲;1kg/m3×V乙=7.8g/cm3×V乙-272kg
解得:V乙=40cm3; 铁块乙的质量:m乙=ρ铁V乙=7.8g/cm3×40cm3 =312g。
2.B
【解析】冰在熔化过程中质量保持不变,根据阿基米德原理分别计算出在液体中的V排 , 再根据密度公式计算出熔化成水的体积,其中V水设冰的质量为m,熔化成水的体积为:;
①浓盐水:冰在浓盐水中漂浮,此时它受到的浮力F浮=G=mg;
那么它排开盐水的体积:;
因为水的密度小于盐水的密度,所以V水>V排 , 则冰熔化后盐水的水面升高;
②酒精:冰在酒精中下沉, 那么它排开盐水的体积:;
因为水的密度大于冰的密度, 所以V水③水:冰在水中漂浮, 此时它受到的浮力F浮=G=mg;
那么它排开水的体积:; 所以V水=V排'', 则冰熔化后水面不变。
3.C
【解析】(1)四个容器中容器底部受到的压强都由水产生,根据公式p=ρ液gh判断大小即可;
(2)上下粗细一致的柱体容器,液体对容器底部的压力等于液体的重力,然后根据G=mg比较液体质量大小,进而判断容器的总质量的大小关系;
(3)当浮力不变时,根据阿基米德原理判断V排的大小;
(4)冰块熔化前后,其质量不变,比较冰块的V排和熔化成的水的体积大小即可;
(5)根据浮沉条件,分析液体密度密度的变化对小球浮沉的影响。
【解答】②四个容器中,物体都没有与底部接触,因此容器底部受到的压强都由水产生。根据公式p=ρ液gh可知,因为水面相平,所以容器底部受到的压强相等,故②正确;
①根据公式F=pS可知,容器的底面积相等,那么容器底部受到的压力相等;根据“上下粗细一致的柱体容器,液体对容器底部的压力等于液体的重力”可知,水和物体的总重力都相等,也就是总质量相等;因为容器的质量相等,所以每个容器的总质量都相等,故①正确;
③如果在b中倒入酒精,那么混合液体的密度减小,而浮力不变;根据公式F浮=ρ液gV排可知,木块自爱液面下的体积增大,故③错误;
④c容器中,冰排开水的体积为:;
冰熔化成水后重力不变,那么水的体积为:;
因为V排=V水 , 即水面高度不变,故④错误;
⑤d中小球现在悬浮,说明ρ水=ρ球;倒入酒精后,混合液体的密度减小,此时ρ水<ρ球, 因此小球下沉,故⑤正确。
那么正确的是①②⑤。
4.B
【解析】根据浮沉条件比较花盆受到浮力的大小关系;首先根据F浮=ρ液gV排判断花盆排开水的体积变化,然后根据公式判断水面的高度变化。
根据浮沉条件可知,
当花盆漂浮时,花盆受到的浮力等于重力;
当花盆下沉到水槽底部时,花盆受的浮力小于重力,
因此沉到水槽底部的花盆所受到的浮力比漂浮时花盆所受到的浮力小;
根据公式F浮=ρ液gV排可知,花盆受到的浮力减小,那么花盆排开水的体积减小;
根据可知,容器的底面积S不变,V排减小,那么液面的高度减小。
5.C
【解析】(1)当两个球完全浸没在水中保持静止时,它们受到的绳的拉力、自重和受到的浮力之间的关系为:G=F拉+F浮;
(2)首先根据密度公式分析两个球的体积大小,然后再根据阿基米德原理判断二者受到浮力的大小;根据相互作用力的原理可知,即可知道两个球对水的压力大小关系,最后根据台秤示数=G容器+G水+F压判断即可。
【解答】(1)根据公式可知,
当质量相等时,因为ρ铅>ρ铝 ,所以V铅根据公式F浮=ρ液V排g可知,当二者浸没时,受到的浮力F浮铅根据G=mg可知,两球的种类G相等;
根据公式G=F拉+F浮可知,绳的拉力T1>T2;
(2)根据相互作用力原理可知,球对水的压力等于球受到的浮力;
因为F浮铅根据公式台秤示数=G容器+G水+F压可知,
当容器重力和水的重力相同时,甲、乙两个台秤的示数N1<N2 。
6.(1)解:因为空桶漂浮在水面,所以F浮=G桶=10N
(2)解:上升;
F浮总=ρ液gV排=1×103Kg/m3×10N/kg×6×10-3m3=60N
G石=F浮总-G桶=60N-10N=50N
m石= =5kg
【解析】(1)当物体漂浮在液面上时,它受到的浮力等于重力,根据浮沉条件计算出空桶受到的浮力;
(2)首先比较鹅卵石受到的浮力的变化,再根据阿基米德原理F浮=ρ液gV排分析它排开水的体积变化,进而确定水面高度的变化。
首先根据阿基米德原理F浮=ρ液gV排计算桶受到的浮力,再根据二力平衡G石=F浮总-G桶计算出鹅卵石的重力,最后根据公式 计算鹅卵石的质量。
【解答】(1)因为空桶漂浮在水面,所以F浮=G桶=10N;
(2)鹅卵石原来在水里下沉,那么F浮桶和鹅卵石受到的浮力F浮总=ρ液gV排=1×103Kg/m3×10N/kg×6×10-3m3=60N;
鹅卵石的重力:G石=F浮总-G桶=60N-10N=50N;
鹅卵石的重力 。
7.(1)500 Pa;(2)4N;(3)6N
【解析】
【分析】
【详解】
解:(1)如图所示,木块下表面的深度为15cm,由题意知,木块的边长为10cm,木块上表面的深度为
h=15cm-10cm=5cm=5×10-2m
木块上表面处的压强为
p=ρ水gh=1.0×103kg/m3×10N/kg×5×10-2m=500Pa
(2)如图所示木块完全浸没,木块的体积就是排开液体体积为
V排=V=(10cm)3=1000cm3=1×10-3m3
由阿基米德原理可得,物体的浮力为
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1×10-3m3=10N
木块重力为
G=m木g=ρ木Vg=0.6×103kg/m3×1×10-3m3×10N/kg=6N
木块处于静止状态,受平衡力作用,所以可得
F浮=F拉+G
细线对木块的拉力为
F拉=F浮-G=10N-6N=4N
(3)因为木块的密度小于水的密度,细线剪断后,木块上浮最后漂浮在水面上,此时受力平衡,木块受到的浮力等于木块的重力为
F浮1=G=6N
答:(1)木块上表面处的压强为500Pa;
(2)细线的拉力为4N;
(3)细线剪断后,木块静止时,木块所受的浮力为6N。
1.B
【解析】(1)四个容器上下粗细一致,那么液体对容器底部的压力等于自身重力,据此判断四个容器中水和物体的总重力的大小关系,根据G=mg确定水和物体总质量的关系,最后根据容器的总质量=水的质量+物体质量+容器质量进行判断即可;
(2)当浮力不变时,根据公式F浮=ρ水gV排可知,木块进入水下的体积与它的密度成反比;
(3)比较冰块排开水的体积和熔化成水的体积大小关系即可;
(4)分析水的密度的变化,再根据浮沉条件进行判断即可。
【解答】①四个容器上下粗细一致,容器的底面积S相等,水面高度相等,
根据公式F=pS=ρ水ghS可知,容器底部受到的压力相等;
因为容器底部受到的压力等于液体和物体的重力之和,
所以四个容器中水和物体的总重力相等;
根据公式G=mg可知,水和物体的总质量相等;
根据容器的总质量=水的质量+物体的质量+容器质量可知,
每个容器的总质量相等,故①正确;
②木块在水面漂浮,
那么它受到的浮力始终等于重力,即保持不变;
b容器中倒入酒精后,水的密度会减小;
根据公式F浮=ρ水gV排可知,木块在液面下的体积变大,故②错误;
③冰块在水面漂浮,
它排开水的体积为:;
冰块熔化后,质量不变,即重力不变,
那么水的体积为:;
因为V排=V,所以熔化后水面高度不变,故③错误;
④小球在d中悬浮,那么它的密度等于水的密度;
d容器中倒入酒精,水的密度减小,
因为水的密度小于小球的密度,所以小球将下沉。
故④正确。
2.C
【解析】
A.剪断绳子前,容器底受到水的压强 p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa
水对容器底部的压力 F=pS=3000Pa×300×10-4m2=90N
故A错误;
B.容器内水的体积 V水=Sh-VB=300cm2×30cm-(10cm)3=8000cm3
容器内水的质量 m水=ρ水V水=1.0g/cm3×8000cm3=8000g=8kg
因水平面上物体的压力和自身的重力相等,且薄壁柱形盛水容器A的质量不计,所以,剪断绳子前,容器对水平地面的压力 F=G总=(m水+mB)g=(8kg+0.4kg)×10N/kg=84N
故B错误;
C.剪断绳子,待物块静止后漂浮在水面上,受到的浮力 F浮=GB=mBg=0.4kg×10N/kg=4N
木块漂浮时排开水的体积 =4×10-4m3
液面下降的深度
水对容器底压强的变化量
Δp=ρ水gΔh=1.0×103kg/m3×10N/kg×0.02m=200Pa
故C正确;
D.剪断绳子,待物块静止后漂浮在水面上时,B的质量和水的质量均不变,由
F=G=mg
可知,水平地面受到的压力不变,水平地面受到的压强不变,即压强的变化量为0Pa,故D错误。
3.B
【解析】【分析】(1)小球受到重力、弹力以及浮力作用,而弹力大小等于重力与浮力的差;
(2)阿基米德原理F浮=gV排。
【解答】小球受到重力、弹力以及浮力作用,而弹力大小等于重力与浮力的差;当地球引力减为一半时,g将变为原来的一半,而F浮=gV排, 因此浮力也减为原来的一半, 即重力与浮力之差变为原来的一半, 因此弹簧被压缩的长度变为原来的一半。
故选B。
4.(1)大于(2)500Pa(3)1.3×103kg/m3
【解析】【分析】(1)对木块进行受力分析,根据二力平衡的知识比较浮力和重力的大小;
(2)根据计算出液体对容器底部的压强变化;
(3)根据相互作用力的原理可知,剪断细绳前,容器底部压力的增大量等于物块受到的浮力;剪断细线后,容器底部压力的增大量等于物块的重力,而二者之差就是电子秤示数的变化量,据此列出方程计算即可。
【解答】(1)在剪断细绳前,物块受到竖直向下的重力和拉力,竖直向上的浮力,根据二力平衡的条件得到:F浮力=G+F拉,则物块受到的浮力大于重力。
(2)剪断细绳厚,液体对容器底部压力的减小量等于电子秤示数的减小量,
即△F=△G=0.5kg×10N/kg=5N;
则液体对容器底部的压强变化了:;
(3)根据相互作用力的原理可知,剪断细绳前,容器底部压力的增大量等于物块受到的浮力,
即F浮力=ρ液gV排;
剪断细绳后,容器底部压力的增大量等于物体的重力,
即F浮力'=G;
二者之差就是电子秤示数的变化量,
即ρ液gV排-G=△G;
ρ液×10N/kg×10-3m3-8N=5N;
解得:ρ液=1.3×103kg/m3。
5.(1)6N;(2)2.4N;(3)360Pa
【解析】
【详解】
(1)由于木块完全浸没在水中,所以排开水的体积为
V排=V木=600cm3=6×10-4m3
木块所受的浮力为
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×6×10-4m3=6N
(2)由可得木块的质量为
m木=ρ木V木=0.6g/cm3×600cm3=360g=0.36kg
木块的重力为
G木=m木g=0.36kg×10N/kg=3.6N
对木块进行受力分析可知,木块受到重力、浮力和拉力的作用,根据力的平衡可知
F浮=F拉+G
所以,绳子对木块的拉力为
F拉=F浮-G=6N-3.6N=2.4N
(3)细线剪断后,当木块静止时,木块处于漂浮状态,则
F浮′=G=3.6N
根据F浮=ρ水gV排可得木块排开水的体积为
根据V=Sh知木块底部的深度为
木块底部所受水的压强为
p=ρ水gh=1.0×103kg/m3×10N/kg×0.036m=360Pa
答:(1)木块所受的F浮大小为6N;
(2)细线对木块的拉力F大小为2.4N;
(3)木块底部所受水的压强为360Pa。
2023浙教版科学七升八暑期“快人一步”培优讲义(四)
浮力(3)--沉浮综合
1.原则:对于复杂情况,我们一般先进行受力分析,然后再代入公式计算。
2.压力差法:F=F-F。
3.阿基米德原理公式:F=G=ρgV
4.平衡法:F=G,该公式只有在物体悬浮、漂浮于液体表面的时候才成立。
5.受力分析:F=G-F,物体在浮力、重力、向下的压力下处于平衡态,那么浮力公式就是:F=G+F。
二、绳子、弹簧等受力分析
物体在液体中处于稳定状态,通常会受到重力、浮力、拉力(弹力)、支持力等作用,先利用二力平衡的条件受力分析,进一步答题。
【能力拓展】
浮力计算基本步骤
①确定研究对象
②确定物体运动状态
③确定物体受力情况
④确定计算方法
三、 液面高度变化问题
类型一:冰漂在某液体
(1)纯冰在纯水中融化,融化后液面高度不变;
(2)纯冰在盐水(或其他密度比水大的液体)中融化,融化后液面升高;
(3)纯冰在密度比水小的液体中融化,融化后液面高度降低。
类型二:冰块中含有其他杂质,漂在水中
(1)含有木块(或其他密度比水小的固体)的冰块在纯水中融化,融化后液面高度不变;
(2)含有石块(或其他密度比水大的固体)的冰块在纯水中融化,融化后液面高度下降;
(3)含有煤油(或其他密度比水小的液体)的冰块在纯水中融化,融化后液面高度上升。
类型三:冰块中含有一定质量的气体,漂在水中,融化后液面下降
【能力拓展】
一、判断方法
(1)比较体积变化法:比较的是冰熔化前(或物体投放前)在液体中排开液体的体积和冰熔化成水后的体积(或物体投放后液体体积)的大小关系:若前体积大于后体积,液面下降;若前体积等于后体积,液面不变;若前体积小于后体积,液面上升。
(2)比较压力变化法:比较前后容器底部受到压力的变化。F前=P前 x S底 = p液gh前S底,F后=P后 x S底 = p液gh后S底,根据前后压力的大小关系得出液体前后深度的关系,再判断液面的升降情况。
(3)比较浮力变化法:比较前后浮力的变化判断液面的升降。若F前浮>F后浮,则液面下降;若F前浮
(1)状态法:变化前后液体中的物体所处的状态进行比较来判断液面的升降。
(2)如何用“状态法”速断液面升降
a.若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;
b.若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;
c.若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高。
例1、如图所示,某圆柱形薄壁容器装有适量的水,其底面积为20cm2 , 将物体B放入水中时,通过台秤测得总质量150g;使用一绳子提起物体B,物体B刚好有一半体积露出水面时保持静止不动,此时台秤示数为70g,并测得容器内液面下降了1cm。则物体B的密度是( )
A.1.5×103kg/m3 B.2.0×103kg/m3 C.2.5×103kg/m3 D.3.0×103kg/m3
例2、如图所示,在一个装满水的容器中,轻质弹簧的一端连着小球,另一端固定在容器底部。已知小球的体积是500cm3,小球静止时受到弹簧对它的作用力为4N。则:
(1)此时小球受到的浮力为多少?
(2)如果剪断弹簧后,请分析小球的运动情况,并计算再次静止后小球受到的浮力是多少?
例3、如图甲所示为一个浮力感应装置,竖直细杆的上端通过力传感器连在天花板上,传感器可以显示出细杆的上端受到作用力的大小,下端与物体M相连,水箱的质量为0.8kg,细杆及连接处的重力可忽略不计,向图甲所示的空水箱中加水直到刚好加满,图乙是力传感器的示数大小随水箱中加入水质量变化的图像:求:
(1)物体M受到的重力?
(2)物体M被浸没时,受到的浮力多少N?
(3)当向容器中加水2.1kg时,传感器的示数为F0,F0大小为多少牛?
(4)当传感器示数变为3F0时,水箱对地面的压力为多少牛?
1.如图所示,在一块浮在水面的长方体木块上放一质量为272克的铁块甲,木块恰好浸没在水中。拿掉铁块甲,用细线把铁块乙系在木块下面,木块也恰好浸没在水中,则铁块乙的质量为( )(ρ铁=7.8克/厘米3 , ρ水=1.0克/厘米3)
A.312克 B.237克 C.318克 D.326克
2.学了浮力知识后,小刚同学想探究冰在不同液体中熔化后的液面升降情况,他用如图的方法,把冰块分别放入浓盐水、酒精,水中,结果熔化后液面比原来下降的是( )
A.盐水 B.酒精 C.水 D.无法判断
3.如图,四个相同的容器内水面一样高,a容器内有水,b容器内有木块漂浮在水面上,c容器内漂浮着一块冰块,d容器中悬浮着一个空心球。下列四种说法正确的一组是()
①每个容器的总质量都相等;②四个容器中,液体对容器底的压强相同;③在 b 容器中倒入酒精后,木块在液面下的体积减小;④c 容器中冰块融化后水面高度将下降;⑤d 容器中倒入酒精后,小球将下沉。
A.①②④ B.①③⑤ C.①②⑤ D.②③④
4.如图为底部有一小孔的花盆倒扣在水槽中,小明发现塑料花盆缓慢下沉直至沉入水槽 底部,这个过程中花盆受到的浮力和水槽中液面的高度变化正确的是( )
A.浮力变大,液面高度下降 B.浮力变小,液面高度下降
C.浮力变大,液面高度上升 D.浮力变小,液面高度上升
5.如图所示,两只完全相同的容器分别装等质量的水放在台秤上,用细线悬挂着质量相同的实心铅球和铝球,逐渐将它们全部浸没在水中(球未接触到容器底,水未溢出),此时台秤甲、乙示数分别为N1和N2 , 绳的拉力分别为T1和T2 , 已知ρ铅>ρ铝 , 则下列关系正确的是( )
A.N1=N2 T1>T2 B.N1>N2 T1>T2 C.N1<N2 T1>T2 D.N1>N2 T1<T2
6.小金把家里景观水池底部的鹅卵石取出清洗他先将一个重为10N的空桶漂浮在水面上,然后将池底的鹅卵石捞出放置在桶内,桶仍漂浮在水面(不考虑捞出过程中带出的水,ρ水=1.0×103kg/m3)
(1)空桶漂浮在水面时所受浮力大小
(2)鹅卵石捞出放置在桶内时,水池水面高度与鹅卵石未捞出时相比会 (选填“上升”、“下降”或“不变”)。若此时桶排开水的体积为6.0×10-3m3 , 求桶内鹅卵石的质量。
7.一边长为10cm,密度为0.6g/cm3的正方体木块,用细线置于容器的水中,此时木块下表面到水面的距离为15cm,如图所示,求:
(1)木块上表面处的压强大小;
(2)细线的拉力大小;
(3)细线剪断后,木块静止时,木块所受的浮力大小?
1.如下图所示,四个相同的容器内水面一样高,a容器内只有水,b容器内有木块漂浮在水面上,c容器内漂浮着一块冰块,d容器中悬浮着一个空心球。则下列四种说法正确的一组是( )
① 每个容器的总质量都相等
② b容器中再倒入酒精后,木块在液面下的体积减小
③ c容器中冰块熔化后水面高度升高
④ d容器中再倒入酒精后,小球将下沉
A.③④ B.①④ C.①② D.②④
2.如图所示水平地面上有底面积为,质量不计的薄壁柱形盛水容器A,内有质量为,边长为,质量分布均匀的正方体物块B,通过一根的细线与容器底部相连,此时水面距容器底,剪断绳子后,木块最终静止时有的体积露出水面,计算可得出( )
A.剪断绳子前,水对容器底部的压力为
B.剪断绳子前,容器对水平地面的压力是
C.剪断绳子,待物块静止后漂浮在水面上,水平地面受到的压强变化了
D.剪断绳子,待物块静止后漂浮在水面上,水对容器底的压强变化了
3.如图,一个弹簧一端固定物体,另一端固定在容器底部,放在装满水的装置中处于静止.设想从某一天起,地球的引力减为一半,则弹簧对物体的弹力(弹簧处于压缩状态)( )
A.不变 B.减为一半
C.增加为原值两倍 D.弹簧对物体无弹力
4.如图所示,将重为 8 N 的物块用细绳拴在装有某液体的容器底部,已知容器底部的面积为 100 cm2,物块的体积为 1 dm3。剪断细绳,电子秤的示数变化了 0.5 kg。求:
(1)剪断细绳前,物块所受的浮力 (选填“小于”“等于”或“大于”)物块的重力。
(2)剪断细绳后,液体对容器底部的压强变化了 。
(3)液体的密度为 。
5.如图所示,用细线系着体积为600cm3、密度为0.6g/cm3的长方体木块,静置于水中(水的密度为1.0×103kg/m3)。求:
(1)木块所受的F浮大小。
(2)细线对木块的拉力F大小。
(3)若木块上下底的面积均为100cm2,剪断细线后,求木块最终静止时,其底部所受水的压强大小(木块最终静止时上下底面与水面平行)。
答案及解析
例1、C
【解析】台秤的示数等于上面物体的总重力,据此列出两种情况下台秤示数与重力的等量关系式,然后通过推导得到B的体积和质量,最后根据密度公式计算即可。
【解答】第一次通过磅秤测得总质量150g,
那么上面的总重力G=mg=0.15kg×10N/kg; 即G杯+G水+GB=1.5N…①
第二次此时磅秤示数为70g;
那么上面的总重力G'=m'g=0.07×10N/kg=0.7N;
设全部浸入时浮力为F浮 , 这里一半体积浸入,故此时的浮力为 ,
则G杯+G水+F浮=0.7N…②
由①-②得,GB- F浮=0.8N…③,
由“物体B刚好有一半体积露出水面时保持静止不动,测得容器内液面下降了1cm。”
可得: ; 解得:V=4×10-5m3;
原来受到的浮力: F浮=ρ水gV排=1.0×103kg/m3×10N/kg×4×10-5m3=0.4N;
将F浮=0.4N代入③, 解得:GB=1N;
则B的质量为:;
物体B的密度。
例2、(1)物体浸没时, V排=V物,利用阿基米德原理公式 F浮=ρ液g V排求出 此时小球受到的浮力;(2) 小球静止时对其进行受力分析可分为二种情况:一种情况是 小球下沉至容器底部静止,求出浮力;另一种情况是小球上浮至水面处于飘浮状态。
例3、(1)2N;(2)10N;(3)1.5N;(4)47.5N
【解析】
【详解】
解:(1)由图乙可知,水箱中没有水时(m=0),压力传感器受到的拉力F1=2N,则物体M的重力
G=F1=2N
(2)由图乙可知,当M完全浸没时,压力传感器的示数为
F2=8N>2N
细杆对传感器的作用力为压力,故传感器对细杆有向下的作用力
F=F2=8N
作用于物体M:此时物体M受到竖直向上的浮力、竖直向下的重力和杆的作用力,处于静止状态,则M受到的浮力
F浮=G+F=2N+8N=10N
(3)综上可知,加水2kg时水面达到M的下表面(此时浮力为0),加水4kg时M刚好浸没(此时浮力为10N),该过程中增加水的质量为2kg,浮力增大了10N,所以,每加1kg水,物体M受到的浮力增加5N;当向水箱中加入质量为2.1kg的水时,受到的浮力
则此时杆的作用力为拉力,力传感器的示数
F0=G-F浮1=2N-0.5N=1.5N
(4)继续向水箱中加水,当力传感器的示数大小变为3F0时,即
F3=3F0=3×1.5N=4.5N>2N
由此可知,此时杆的作用力为压力,物体M受到的浮力
F浮2=G+F3=2N+4.5N=6.5N
此时容器内水的质量
m水2=2kg+6.5N×1kg/5N=3.3kg
把水箱和水、物体M看做整体,受力分析可知,受到竖直向下的总重力和杆向下的压力3F0、水平面的支持力作用处于平衡状态,由整体受到的合力为零可得
F支持=(m水2+m水箱)g+G+F3=(3.3kg+0.8kg)×10N/kg+2N+4.5N=47.5N
此时水箱对水平面的压力
F压=F支持=47.5N
答:(1)物体M受到的重力为2N;
(2)物体M被浸没时,受到的浮力为10N;
(3)当向容器中加水2.1kg时,传感器的示数为F0,F0大小为1.5N;
(4)当传感器示数变为3F0时,水箱对地面的压力为47.5N。
1.A
【解析】由甲图可知木块和甲铁块漂浮,由乙图可知木块和乙铁块悬浮,根据物体的浮沉条件和阿基米德原理得出等式,即可求出乙铁块的体积,再根据m=ρV求出铁块乙的质量。
【解答】木块和甲铁块在水面漂浮,
那么F浮甲=G甲+G木;
即ρ水gV木=m甲g+G木 ①;
木块和乙铁块在水中悬浮, 那么F浮乙=G乙+G木;
即ρ水g(V木+V乙)=ρ铁gV乙+G木 ②;
②-①得到:ρ水gV乙=ρ铁gV乙-m甲g;
ρ水V乙=ρ铁V乙-m甲;1kg/m3×V乙=7.8g/cm3×V乙-272kg
解得:V乙=40cm3; 铁块乙的质量:m乙=ρ铁V乙=7.8g/cm3×40cm3 =312g。
2.B
【解析】冰在熔化过程中质量保持不变,根据阿基米德原理分别计算出在液体中的V排 , 再根据密度公式计算出熔化成水的体积,其中V水
①浓盐水:冰在浓盐水中漂浮,此时它受到的浮力F浮=G=mg;
那么它排开盐水的体积:;
因为水的密度小于盐水的密度,所以V水>V排 , 则冰熔化后盐水的水面升高;
②酒精:冰在酒精中下沉, 那么它排开盐水的体积:;
因为水的密度大于冰的密度, 所以V水
那么它排开水的体积:; 所以V水=V排'', 则冰熔化后水面不变。
3.C
【解析】(1)四个容器中容器底部受到的压强都由水产生,根据公式p=ρ液gh判断大小即可;
(2)上下粗细一致的柱体容器,液体对容器底部的压力等于液体的重力,然后根据G=mg比较液体质量大小,进而判断容器的总质量的大小关系;
(3)当浮力不变时,根据阿基米德原理判断V排的大小;
(4)冰块熔化前后,其质量不变,比较冰块的V排和熔化成的水的体积大小即可;
(5)根据浮沉条件,分析液体密度密度的变化对小球浮沉的影响。
【解答】②四个容器中,物体都没有与底部接触,因此容器底部受到的压强都由水产生。根据公式p=ρ液gh可知,因为水面相平,所以容器底部受到的压强相等,故②正确;
①根据公式F=pS可知,容器的底面积相等,那么容器底部受到的压力相等;根据“上下粗细一致的柱体容器,液体对容器底部的压力等于液体的重力”可知,水和物体的总重力都相等,也就是总质量相等;因为容器的质量相等,所以每个容器的总质量都相等,故①正确;
③如果在b中倒入酒精,那么混合液体的密度减小,而浮力不变;根据公式F浮=ρ液gV排可知,木块自爱液面下的体积增大,故③错误;
④c容器中,冰排开水的体积为:;
冰熔化成水后重力不变,那么水的体积为:;
因为V排=V水 , 即水面高度不变,故④错误;
⑤d中小球现在悬浮,说明ρ水=ρ球;倒入酒精后,混合液体的密度减小,此时ρ水<ρ球, 因此小球下沉,故⑤正确。
那么正确的是①②⑤。
4.B
【解析】根据浮沉条件比较花盆受到浮力的大小关系;首先根据F浮=ρ液gV排判断花盆排开水的体积变化,然后根据公式判断水面的高度变化。
根据浮沉条件可知,
当花盆漂浮时,花盆受到的浮力等于重力;
当花盆下沉到水槽底部时,花盆受的浮力小于重力,
因此沉到水槽底部的花盆所受到的浮力比漂浮时花盆所受到的浮力小;
根据公式F浮=ρ液gV排可知,花盆受到的浮力减小,那么花盆排开水的体积减小;
根据可知,容器的底面积S不变,V排减小,那么液面的高度减小。
5.C
【解析】(1)当两个球完全浸没在水中保持静止时,它们受到的绳的拉力、自重和受到的浮力之间的关系为:G=F拉+F浮;
(2)首先根据密度公式分析两个球的体积大小,然后再根据阿基米德原理判断二者受到浮力的大小;根据相互作用力的原理可知,即可知道两个球对水的压力大小关系,最后根据台秤示数=G容器+G水+F压判断即可。
【解答】(1)根据公式可知,
当质量相等时,因为ρ铅>ρ铝 ,所以V铅
根据公式G=F拉+F浮可知,绳的拉力T1>T2;
(2)根据相互作用力原理可知,球对水的压力等于球受到的浮力;
因为F浮铅
当容器重力和水的重力相同时,甲、乙两个台秤的示数N1<N2 。
6.(1)解:因为空桶漂浮在水面,所以F浮=G桶=10N
(2)解:上升;
F浮总=ρ液gV排=1×103Kg/m3×10N/kg×6×10-3m3=60N
G石=F浮总-G桶=60N-10N=50N
m石= =5kg
【解析】(1)当物体漂浮在液面上时,它受到的浮力等于重力,根据浮沉条件计算出空桶受到的浮力;
(2)首先比较鹅卵石受到的浮力的变化,再根据阿基米德原理F浮=ρ液gV排分析它排开水的体积变化,进而确定水面高度的变化。
首先根据阿基米德原理F浮=ρ液gV排计算桶受到的浮力,再根据二力平衡G石=F浮总-G桶计算出鹅卵石的重力,最后根据公式 计算鹅卵石的质量。
【解答】(1)因为空桶漂浮在水面,所以F浮=G桶=10N;
(2)鹅卵石原来在水里下沉,那么F浮
鹅卵石的重力:G石=F浮总-G桶=60N-10N=50N;
鹅卵石的重力 。
7.(1)500 Pa;(2)4N;(3)6N
【解析】
【分析】
【详解】
解:(1)如图所示,木块下表面的深度为15cm,由题意知,木块的边长为10cm,木块上表面的深度为
h=15cm-10cm=5cm=5×10-2m
木块上表面处的压强为
p=ρ水gh=1.0×103kg/m3×10N/kg×5×10-2m=500Pa
(2)如图所示木块完全浸没,木块的体积就是排开液体体积为
V排=V=(10cm)3=1000cm3=1×10-3m3
由阿基米德原理可得,物体的浮力为
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1×10-3m3=10N
木块重力为
G=m木g=ρ木Vg=0.6×103kg/m3×1×10-3m3×10N/kg=6N
木块处于静止状态,受平衡力作用,所以可得
F浮=F拉+G
细线对木块的拉力为
F拉=F浮-G=10N-6N=4N
(3)因为木块的密度小于水的密度,细线剪断后,木块上浮最后漂浮在水面上,此时受力平衡,木块受到的浮力等于木块的重力为
F浮1=G=6N
答:(1)木块上表面处的压强为500Pa;
(2)细线的拉力为4N;
(3)细线剪断后,木块静止时,木块所受的浮力为6N。
1.B
【解析】(1)四个容器上下粗细一致,那么液体对容器底部的压力等于自身重力,据此判断四个容器中水和物体的总重力的大小关系,根据G=mg确定水和物体总质量的关系,最后根据容器的总质量=水的质量+物体质量+容器质量进行判断即可;
(2)当浮力不变时,根据公式F浮=ρ水gV排可知,木块进入水下的体积与它的密度成反比;
(3)比较冰块排开水的体积和熔化成水的体积大小关系即可;
(4)分析水的密度的变化,再根据浮沉条件进行判断即可。
【解答】①四个容器上下粗细一致,容器的底面积S相等,水面高度相等,
根据公式F=pS=ρ水ghS可知,容器底部受到的压力相等;
因为容器底部受到的压力等于液体和物体的重力之和,
所以四个容器中水和物体的总重力相等;
根据公式G=mg可知,水和物体的总质量相等;
根据容器的总质量=水的质量+物体的质量+容器质量可知,
每个容器的总质量相等,故①正确;
②木块在水面漂浮,
那么它受到的浮力始终等于重力,即保持不变;
b容器中倒入酒精后,水的密度会减小;
根据公式F浮=ρ水gV排可知,木块在液面下的体积变大,故②错误;
③冰块在水面漂浮,
它排开水的体积为:;
冰块熔化后,质量不变,即重力不变,
那么水的体积为:;
因为V排=V,所以熔化后水面高度不变,故③错误;
④小球在d中悬浮,那么它的密度等于水的密度;
d容器中倒入酒精,水的密度减小,
因为水的密度小于小球的密度,所以小球将下沉。
故④正确。
2.C
【解析】
A.剪断绳子前,容器底受到水的压强 p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa
水对容器底部的压力 F=pS=3000Pa×300×10-4m2=90N
故A错误;
B.容器内水的体积 V水=Sh-VB=300cm2×30cm-(10cm)3=8000cm3
容器内水的质量 m水=ρ水V水=1.0g/cm3×8000cm3=8000g=8kg
因水平面上物体的压力和自身的重力相等,且薄壁柱形盛水容器A的质量不计,所以,剪断绳子前,容器对水平地面的压力 F=G总=(m水+mB)g=(8kg+0.4kg)×10N/kg=84N
故B错误;
C.剪断绳子,待物块静止后漂浮在水面上,受到的浮力 F浮=GB=mBg=0.4kg×10N/kg=4N
木块漂浮时排开水的体积 =4×10-4m3
液面下降的深度
水对容器底压强的变化量
Δp=ρ水gΔh=1.0×103kg/m3×10N/kg×0.02m=200Pa
故C正确;
D.剪断绳子,待物块静止后漂浮在水面上时,B的质量和水的质量均不变,由
F=G=mg
可知,水平地面受到的压力不变,水平地面受到的压强不变,即压强的变化量为0Pa,故D错误。
3.B
【解析】【分析】(1)小球受到重力、弹力以及浮力作用,而弹力大小等于重力与浮力的差;
(2)阿基米德原理F浮=gV排。
【解答】小球受到重力、弹力以及浮力作用,而弹力大小等于重力与浮力的差;当地球引力减为一半时,g将变为原来的一半,而F浮=gV排, 因此浮力也减为原来的一半, 即重力与浮力之差变为原来的一半, 因此弹簧被压缩的长度变为原来的一半。
故选B。
4.(1)大于(2)500Pa(3)1.3×103kg/m3
【解析】【分析】(1)对木块进行受力分析,根据二力平衡的知识比较浮力和重力的大小;
(2)根据计算出液体对容器底部的压强变化;
(3)根据相互作用力的原理可知,剪断细绳前,容器底部压力的增大量等于物块受到的浮力;剪断细线后,容器底部压力的增大量等于物块的重力,而二者之差就是电子秤示数的变化量,据此列出方程计算即可。
【解答】(1)在剪断细绳前,物块受到竖直向下的重力和拉力,竖直向上的浮力,根据二力平衡的条件得到:F浮力=G+F拉,则物块受到的浮力大于重力。
(2)剪断细绳厚,液体对容器底部压力的减小量等于电子秤示数的减小量,
即△F=△G=0.5kg×10N/kg=5N;
则液体对容器底部的压强变化了:;
(3)根据相互作用力的原理可知,剪断细绳前,容器底部压力的增大量等于物块受到的浮力,
即F浮力=ρ液gV排;
剪断细绳后,容器底部压力的增大量等于物体的重力,
即F浮力'=G;
二者之差就是电子秤示数的变化量,
即ρ液gV排-G=△G;
ρ液×10N/kg×10-3m3-8N=5N;
解得:ρ液=1.3×103kg/m3。
5.(1)6N;(2)2.4N;(3)360Pa
【解析】
【详解】
(1)由于木块完全浸没在水中,所以排开水的体积为
V排=V木=600cm3=6×10-4m3
木块所受的浮力为
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×6×10-4m3=6N
(2)由可得木块的质量为
m木=ρ木V木=0.6g/cm3×600cm3=360g=0.36kg
木块的重力为
G木=m木g=0.36kg×10N/kg=3.6N
对木块进行受力分析可知,木块受到重力、浮力和拉力的作用,根据力的平衡可知
F浮=F拉+G
所以,绳子对木块的拉力为
F拉=F浮-G=6N-3.6N=2.4N
(3)细线剪断后,当木块静止时,木块处于漂浮状态,则
F浮′=G=3.6N
根据F浮=ρ水gV排可得木块排开水的体积为
根据V=Sh知木块底部的深度为
木块底部所受水的压强为
p=ρ水gh=1.0×103kg/m3×10N/kg×0.036m=360Pa
答:(1)木块所受的F浮大小为6N;
(2)细线对木块的拉力F大小为2.4N;
(3)木块底部所受水的压强为360Pa。
2023浙教版科学七升八暑期“快人一步”培优讲义(四)
浮力(3)--沉浮综合
同课章节目录
