山东省济南市商河县2022-2023学年八年级下学期期末考试数学试题(无答案)
文档属性
| 名称 | 山东省济南市商河县2022-2023学年八年级下学期期末考试数学试题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 00:00:00 | ||
图片预览


文档简介
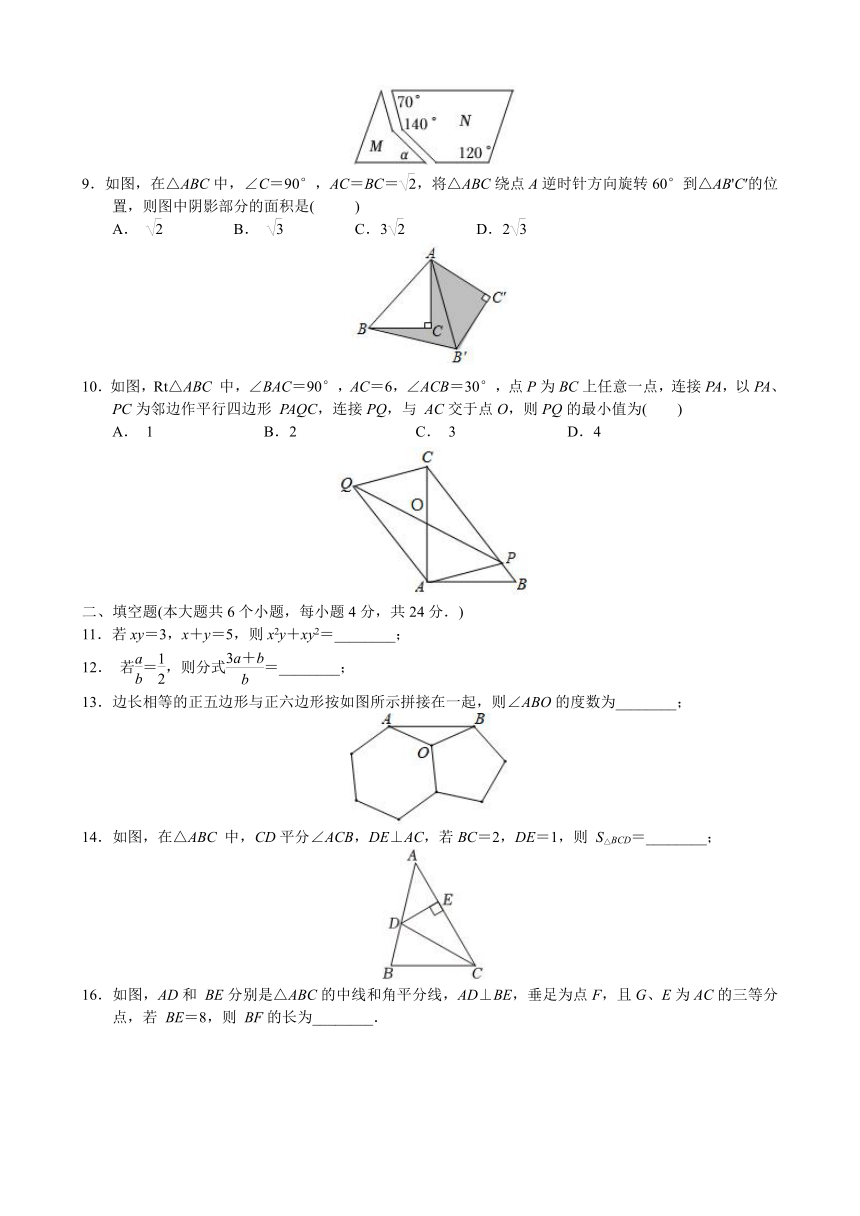
济南市商河县2022~2023 学年第二学期八年级期末考试数学试题
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只一项是符合题目要求的.)
1.下列卡通图标分别是“星球”、“宇航员”、“星系”和“黑洞”,其中是中心对称图形的是( )
B. C. D.
2.已知实数a 和 b,若a<b,则下列结论中,不一定成立的是( )
A.-3a>-3b B.am2<bm2 C.< D.a+m<b+m
3.在下列因式分解的过程中,分解因式正确的是( )
A.x2+2x+4=(x+2) 2 B.x2-4=(x+4) (x-4)
C.x2-4x+4=(x-2)2 D. x2+4=(x+2) 2
4.如果代数式-1的值为0,那么实数x满足( )
A.x=1 B.x≥1 C.x≠0 D.x≥0
5.在Rt△ABC 中,∠C=90°,∠B=22.5°,AB的垂直平分线DE交BC于点E,BE=3,则AC等于( )
A.3 B.6 C.3 D.6
6. 已知x+=6,则x2+=( )
A.38 B.36 C.34 D.32
7.现有一四边形 ABCD,借助此四边形作平行四边形EFGH,两位同学提供了如下方案,对于方案1、II,下列说法正确的是( )
A.I可行、II不可行 B.I不可行、II可行
C.I、II都可行 D.I、II都不可行
方案I: 作边AB,BC,CD,AD的垂直平分线l1,l2,l3,l4,分别交 AB,BC,CD,AD于点E,F,G,H,顺次连接这四点围成的四边形EFGH 即为所求. 方案II: 连接AC,BD,过四边形 ABCD各顶点分别作 AC,BD 的平行线EF,GH,EH,FG,这四条平行线围成的四边形EFGH 即为所求.
8.如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数为( )
A. 20° B. 30° C.40° D. 70°
9.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A逆时针方向旋转60°到△AB'C′的位置,则图中阴影部分的面积是( )
A. B. C.3 D.2
10.如图,Rt△ABC 中,∠BAC=90°,AC=6,∠ACB=30°,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形 PAQC,连接PQ,与 AC交于点O,则PQ的最小值为( )
A. 1 B.2 C. 3 D.4
二、填空题(本大题共6个小题,每小题4分,共24分.)
11.若xy=3,x+y=5,则x2y+xy2=________;
12. 若=,则分式=________;
13.边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为________;
14.如图,在△ABC 中,CD平分∠ACB,DE⊥AC,若BC=2,DE=1,则 S△BCD=________;
16.如图,AD和 BE分别是△ABC的中线和角平分线,AD⊥BE,垂足为点F,且G、E为AC的三等分点,若 BE=8,则 BF的长为________.
三、解答题(本大题共9个小题,共86分.解答题应写出文字说明、证明过程或演算步骤.)
17.(本题满分10分,每小题5分)解不等式(组):
(1)解不等式:2(x+1)-1≥3x+2,并把它的解集在数轴上表示出来;
(2)解不等式组,并写出该不等式组的非负整数解.
18.(本题满分8分,每小题4分)分解因式:
(1) 25x2-36; (2) 2x2y-8xy+8y.
19.(本题满分10分)计算:
(1)-
(2)先化简,再求值(+÷,其中x=-3.
20.(本题满分6分)
如图,平行四边形ABCD中E,F是直线AC上两点,且AE=CF.
求证:BE∥DF.
21.(本题满分8分)
如图,在平面直角坐标系中,点 B的坐标是(0,4),点 A的坐标是(3,1)
(1)将△OAB 先向下平移4个单位长度,再向左平移2个单位长度后得到△O1A1B1,画出△O1A1B1,并直接写出点A1的坐标________;
(2)将△OAB 绕点O 逆时针旋转 90°后得到△OA2B2,画出△OA2B2,并直接写出点 B2 的坐标________;
(3)求(2)中OA扫过的面积.
22.(本题满分10 分)
王老师安排喜欢探究问题的小明同学解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:m2+2mn+2n2-6n+9=0,
∴m2+2mn+n2+n2-6n+9=0.
即(m+n) 2+(n-3) 2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
为什么要对2n2进行了拆项呢 聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程.
(1)若x2-4xy+5y2+2y+1=0,求x的值;
(2)已知a、b、c是等腰△ABC的三边长,且满足a2-10a+b2-12b+61=0,求此三角形的周长.
24.(本题满分10分)
如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与 PA 相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断 DE与 PD的位置关系,并说明理由;
(2)若AC=3,BC=4,PA=1,求线段DE的长,
24.(本题满分12分)
李老师近期准备换车,看中了价格相同的两款国产车.经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的行驶费用比燃油车平均每公里的行驶费用少0.6元,若两款车的行驶费用均为200元时,电动汽车可行驶的总路程是燃油车的4倍,
(1)求这款电动汽车平均每公里的行驶费用;
(2)若电动汽车和燃油车每年的其它费用分别为7800元和4800元.问:每年行驶里程为多少千米时,买电动汽车的年费用更低 (年费用=年行驶费用十年其它费用)
25.(本题满分12分)
综合与实践:
图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图1,在△ABC中,AB=AC,∠BAC=α,D,E 分别为 AB、AC边上一点,连接 DE,且DE∥BC,将△ABC绕点A 在平面内旋转.
(1)观察猜想
若α=60°,将△ABC绕点A 旋转到如图2所示的位置,则 DB与CE的数量关系为________;
(2)类比探究
若α=90°,将△ABC绕点A 旋转到如图3所示的位置,DB,CE相交于点O,猜想DB、CE 满足的位置关系,并说明理由;
(3)拓展应用
如图4,在(2)的条件下,连结CD,分别取DE、DC、BC的中点M、P、N,连结PM、PN、MN,若 AD=4,AB=10,请求出在旋转过程中△PMN面积的最大值.
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只一项是符合题目要求的.)
1.下列卡通图标分别是“星球”、“宇航员”、“星系”和“黑洞”,其中是中心对称图形的是( )
B. C. D.
2.已知实数a 和 b,若a<b,则下列结论中,不一定成立的是( )
A.-3a>-3b B.am2<bm2 C.< D.a+m<b+m
3.在下列因式分解的过程中,分解因式正确的是( )
A.x2+2x+4=(x+2) 2 B.x2-4=(x+4) (x-4)
C.x2-4x+4=(x-2)2 D. x2+4=(x+2) 2
4.如果代数式-1的值为0,那么实数x满足( )
A.x=1 B.x≥1 C.x≠0 D.x≥0
5.在Rt△ABC 中,∠C=90°,∠B=22.5°,AB的垂直平分线DE交BC于点E,BE=3,则AC等于( )
A.3 B.6 C.3 D.6
6. 已知x+=6,则x2+=( )
A.38 B.36 C.34 D.32
7.现有一四边形 ABCD,借助此四边形作平行四边形EFGH,两位同学提供了如下方案,对于方案1、II,下列说法正确的是( )
A.I可行、II不可行 B.I不可行、II可行
C.I、II都可行 D.I、II都不可行
方案I: 作边AB,BC,CD,AD的垂直平分线l1,l2,l3,l4,分别交 AB,BC,CD,AD于点E,F,G,H,顺次连接这四点围成的四边形EFGH 即为所求. 方案II: 连接AC,BD,过四边形 ABCD各顶点分别作 AC,BD 的平行线EF,GH,EH,FG,这四条平行线围成的四边形EFGH 即为所求.
8.如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数为( )
A. 20° B. 30° C.40° D. 70°
9.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A逆时针方向旋转60°到△AB'C′的位置,则图中阴影部分的面积是( )
A. B. C.3 D.2
10.如图,Rt△ABC 中,∠BAC=90°,AC=6,∠ACB=30°,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形 PAQC,连接PQ,与 AC交于点O,则PQ的最小值为( )
A. 1 B.2 C. 3 D.4
二、填空题(本大题共6个小题,每小题4分,共24分.)
11.若xy=3,x+y=5,则x2y+xy2=________;
12. 若=,则分式=________;
13.边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为________;
14.如图,在△ABC 中,CD平分∠ACB,DE⊥AC,若BC=2,DE=1,则 S△BCD=________;
16.如图,AD和 BE分别是△ABC的中线和角平分线,AD⊥BE,垂足为点F,且G、E为AC的三等分点,若 BE=8,则 BF的长为________.
三、解答题(本大题共9个小题,共86分.解答题应写出文字说明、证明过程或演算步骤.)
17.(本题满分10分,每小题5分)解不等式(组):
(1)解不等式:2(x+1)-1≥3x+2,并把它的解集在数轴上表示出来;
(2)解不等式组,并写出该不等式组的非负整数解.
18.(本题满分8分,每小题4分)分解因式:
(1) 25x2-36; (2) 2x2y-8xy+8y.
19.(本题满分10分)计算:
(1)-
(2)先化简,再求值(+÷,其中x=-3.
20.(本题满分6分)
如图,平行四边形ABCD中E,F是直线AC上两点,且AE=CF.
求证:BE∥DF.
21.(本题满分8分)
如图,在平面直角坐标系中,点 B的坐标是(0,4),点 A的坐标是(3,1)
(1)将△OAB 先向下平移4个单位长度,再向左平移2个单位长度后得到△O1A1B1,画出△O1A1B1,并直接写出点A1的坐标________;
(2)将△OAB 绕点O 逆时针旋转 90°后得到△OA2B2,画出△OA2B2,并直接写出点 B2 的坐标________;
(3)求(2)中OA扫过的面积.
22.(本题满分10 分)
王老师安排喜欢探究问题的小明同学解决某个问题前,先让小明看了一个有解答过程的例题.
例:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:m2+2mn+2n2-6n+9=0,
∴m2+2mn+n2+n2-6n+9=0.
即(m+n) 2+(n-3) 2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
为什么要对2n2进行了拆项呢 聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程.
(1)若x2-4xy+5y2+2y+1=0,求x的值;
(2)已知a、b、c是等腰△ABC的三边长,且满足a2-10a+b2-12b+61=0,求此三角形的周长.
24.(本题满分10分)
如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上运动,PD始终保持与 PA 相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断 DE与 PD的位置关系,并说明理由;
(2)若AC=3,BC=4,PA=1,求线段DE的长,
24.(本题满分12分)
李老师近期准备换车,看中了价格相同的两款国产车.经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的行驶费用比燃油车平均每公里的行驶费用少0.6元,若两款车的行驶费用均为200元时,电动汽车可行驶的总路程是燃油车的4倍,
(1)求这款电动汽车平均每公里的行驶费用;
(2)若电动汽车和燃油车每年的其它费用分别为7800元和4800元.问:每年行驶里程为多少千米时,买电动汽车的年费用更低 (年费用=年行驶费用十年其它费用)
25.(本题满分12分)
综合与实践:
图形的旋转变换是研究数学相关问题的重要手段之一,在研究三角形的旋转过程中,发现下列问题:如图1,在△ABC中,AB=AC,∠BAC=α,D,E 分别为 AB、AC边上一点,连接 DE,且DE∥BC,将△ABC绕点A 在平面内旋转.
(1)观察猜想
若α=60°,将△ABC绕点A 旋转到如图2所示的位置,则 DB与CE的数量关系为________;
(2)类比探究
若α=90°,将△ABC绕点A 旋转到如图3所示的位置,DB,CE相交于点O,猜想DB、CE 满足的位置关系,并说明理由;
(3)拓展应用
如图4,在(2)的条件下,连结CD,分别取DE、DC、BC的中点M、P、N,连结PM、PN、MN,若 AD=4,AB=10,请求出在旋转过程中△PMN面积的最大值.
同课章节目录
