完全平方公式[上学期]
图片预览





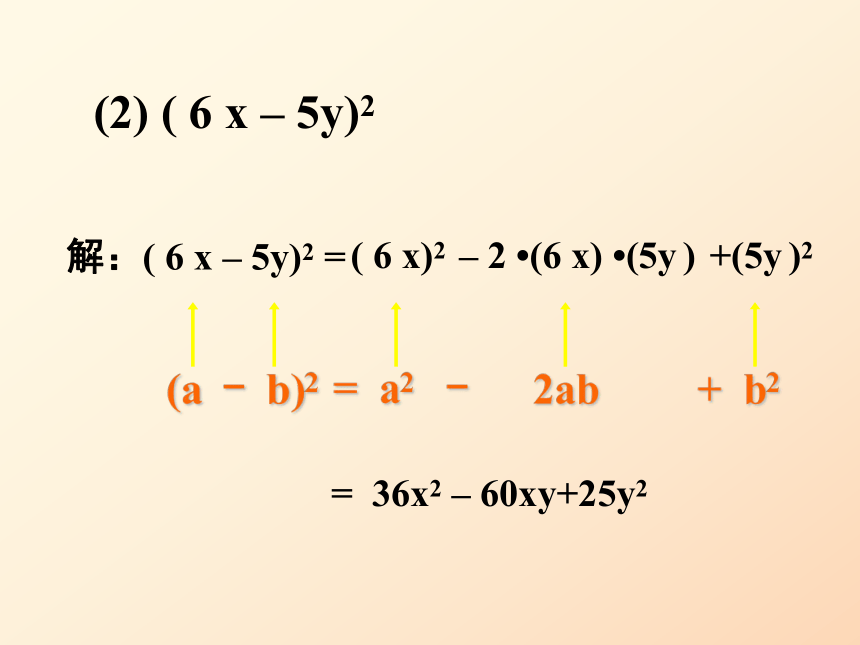
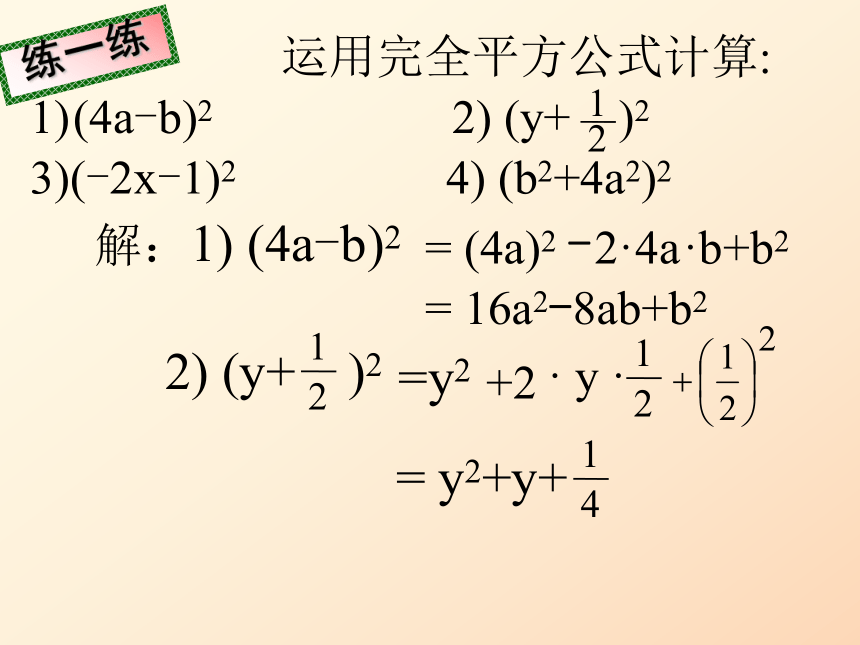
文档简介
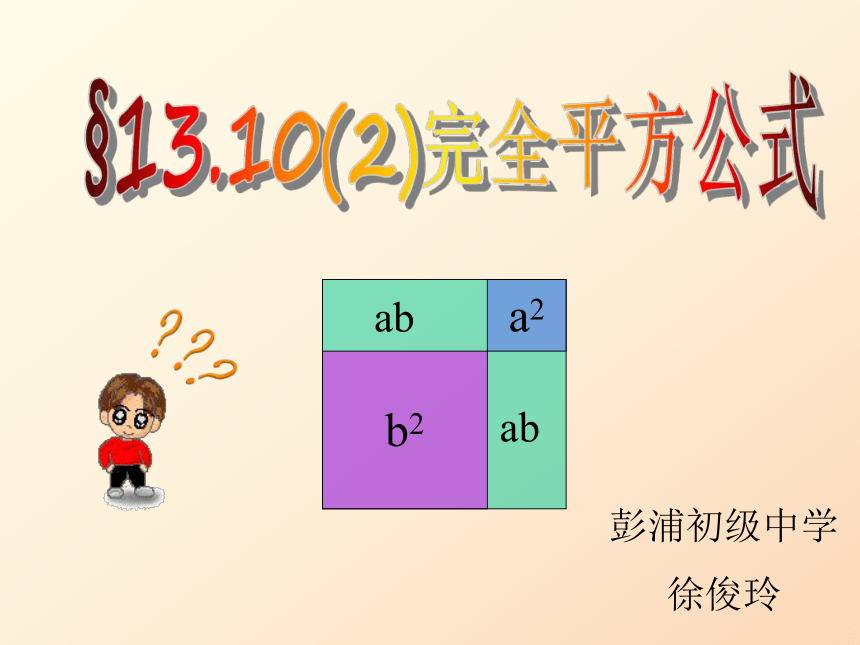
课件26张PPT。§13.10(2)完全平方公式??? ab
b2a2彭浦初级中学
徐俊玲ab多项式乘法公式:1.(a+b)(c+d) =
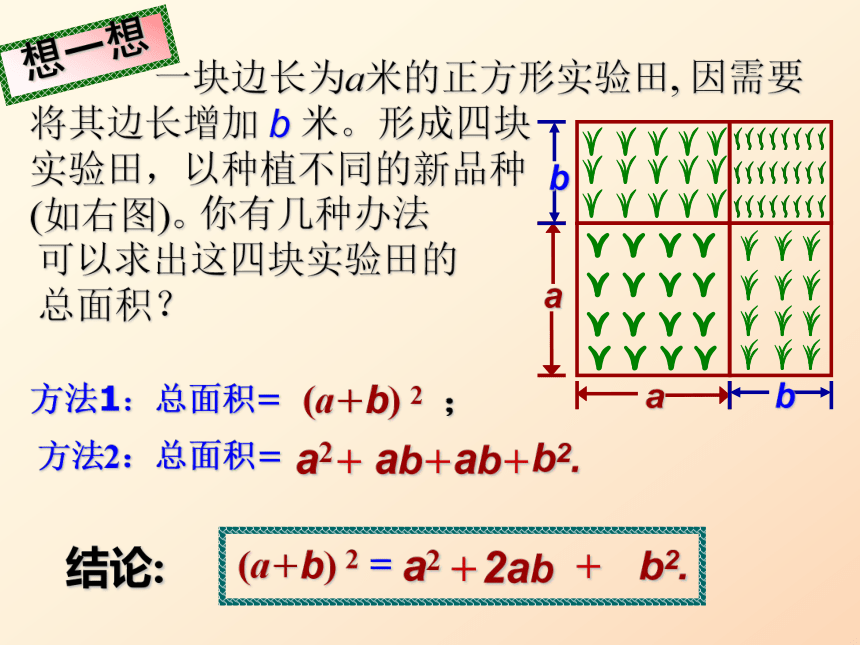
平方差公式:(a+b)(a-b) = a2-b2ac+ad+bc+bd2.(x+a)(x+b) =x2+(a+b)x+ab复习 一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块
实验田,以种植不同的新品种
(如右图)。方法1:总面积= 你有几种办法可以求出这四块实验田的总面积?(a+b) 2 ;方法2:总面积=结论:=(a+b) 2想一想 完全平方公式 (1) 你能用多项式的乘法法则来说明它成立吗?(a+b)2=a2+2ab+b2 ;(a+b) (a+b)
=a2+ab+ab+b2=a2+2ab+ b2(3)a2 ?2ab+b2.小颖写出了如下的算式:(a?b)2=[a+(?b)]2?她是怎么想的?= 2 + 2 + 2 aa(?b)(?b)=a22ab?b2.+你能继续做下去吗?(2) 你能计算它的结果吗?(a+b)2 = a2 + 2ab + b2(a-b)2 = a2 - 2ab + b2
两数和 的平方,等于两数的平方和,
加上 它们的积的两倍.( 差)(减去)完全平方公式:(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2公式的特点:1、积为二次三项式;2、积中首尾两项为两数的平方和;3、中间项是两数积的2倍,且与乘式中
间的符号相同。解: (2x+ 3 )2=( a+ b)2= a2 + 2 a b+ b2=4x2+12x+9(2x)2学一学 例1 利用完全平方公式计算:
(2x+3)2 ; (2) (6x-5y)2 ; +2· 2x· 3+ 32= 36x2 – 60xy+25y2+(5y )2解:( 6 x – 5y)2 =(a - b)2 = a2 - 2ab + b2 ( 6 x)2– 2 ?(6 x) ?(5y )(2) ( 6 x – 5y)2 运用完全平方公式计算:
(4a-b)2 2) (y+ )2
3)(-2x-1)2 4) (b2+4a2)221解:1) (4a-b)2练一练=y2= (4a)2
= 16a2-8ab+b2-2·4a·b+b2+2· y · 3) (-2x-1)2方法一方法二方法三 3) (-2x-1)2方法一解:原式=[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1方法二方法三一二一三 3) (-2x-1)2方法二解:原式=[(-2x)-1]2
= (-2x) 2 - 2· (-2x) ·1+1
=4x2+4x+1方法一方法三一二二三 3) (-2x-1)2方法三解:原式=[(-2x)+(-1)]2
=(-2x)2 + 2·(-2x) ·(-1) + (-1)2
=4x2+4x+1方法二方法一二三一三 3) (-2x-1)2方法一方法二方法三 原式=[(-2x)-1]2
=(-2x)2-2·(-2x)·1+1
=4x2+4x+1原式 =[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1 3) (-2x-1)2方法一方法三方法二原式 =[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1原式=[(-2x)+(-1)]2
=(-2x)2 + 2·(-2x) ·(-1) + (-1)2
=4x2+4x+1 3) (-2x-1)2方法二 原式=[(-2x)-1]2
=(-2x)2-2·(-2x)·1+1
=4x2+4x+1方法三原式=[(-2x)+(-1)]2
=(-2x)2 + 2·(-2x) ·(-1)
+ (-1)2
=4x2+4x+1方法一 3) (-2x-1)2方法一方法二方法三原式=[(-2x)+(-1)]2=(-2x)2+2·(-2x)·(-1)+(-1)2
=4x2+4x+1 原式=[(-2x)-1]2 =(-2x)2-2·(-2x)·1+1
=4x2+4x+1原式 =[-(2x+1)]2 =(2x+1)2
=(2x)2+2·2x·1+1=4x2+4x+1一二一三二三4) (b2+4a2)2解:原式 = (b2)2+2· b2 · (4a2) + (4a2)2
= b4 +8 a2 b2 + 16a4几点注意:1、项数:积的项数为三;2、符号:特别是(a-b)2= a2 - 2ab+b2;3、字母:不要漏写;4、字母指数:当公式中的a、b所代表的
单项式字母指数不是1时,乘方时要记
住字母指数需乘2。练习:下面各式的计算是否正确?如果不正确,应当怎样改正?(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3)(x -y)2 =x2+2xy +y2(4)(x+y)2 =x2 +xy +y2错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2-2xy +y2(x +y)2 =x2+2xy +y2(5)(2a?1)2=2a2?2a+1错 (2a?1)2=4a2?4a+1(6)(?a?1)2=?a2?2a?1.
错(?a?1)2=(?a)2?2?(?a )?1+12例2.运用完全平方公式计算:
1) 1022 2) 1992解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2
=2002-2×200×1+12
= 40000-400+1
= 39601练一练运用完全平方公式计算:
962 2) 1052
3)79.82 4) 80.32
小结注意完全平方公式和平方差公式不同:形式不同.结果不同:完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2. 有时需要进行变形,使变形后的式子符合应用完全平方公式
的条件,即为“两数和(或差)的平方”,然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积。
1.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积。
2.运用完全平方公式计算:
1) 1022 2) 1992再见!
b2a2彭浦初级中学
徐俊玲ab多项式乘法公式:1.(a+b)(c+d) =
平方差公式:(a+b)(a-b) = a2-b2ac+ad+bc+bd2.(x+a)(x+b) =x2+(a+b)x+ab复习 一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块
实验田,以种植不同的新品种
(如右图)。方法1:总面积= 你有几种办法可以求出这四块实验田的总面积?(a+b) 2 ;方法2:总面积=结论:=(a+b) 2想一想 完全平方公式 (1) 你能用多项式的乘法法则来说明它成立吗?(a+b)2=a2+2ab+b2 ;(a+b) (a+b)
=a2+ab+ab+b2=a2+2ab+ b2(3)a2 ?2ab+b2.小颖写出了如下的算式:(a?b)2=[a+(?b)]2?她是怎么想的?= 2 + 2 + 2 aa(?b)(?b)=a22ab?b2.+你能继续做下去吗?(2) 你能计算它的结果吗?(a+b)2 = a2 + 2ab + b2(a-b)2 = a2 - 2ab + b2
两数和 的平方,等于两数的平方和,
加上 它们的积的两倍.( 差)(减去)完全平方公式:(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2公式的特点:1、积为二次三项式;2、积中首尾两项为两数的平方和;3、中间项是两数积的2倍,且与乘式中
间的符号相同。解: (2x+ 3 )2=( a+ b)2= a2 + 2 a b+ b2=4x2+12x+9(2x)2学一学 例1 利用完全平方公式计算:
(2x+3)2 ; (2) (6x-5y)2 ; +2· 2x· 3+ 32= 36x2 – 60xy+25y2+(5y )2解:( 6 x – 5y)2 =(a - b)2 = a2 - 2ab + b2 ( 6 x)2– 2 ?(6 x) ?(5y )(2) ( 6 x – 5y)2 运用完全平方公式计算:
(4a-b)2 2) (y+ )2
3)(-2x-1)2 4) (b2+4a2)221解:1) (4a-b)2练一练=y2= (4a)2
= 16a2-8ab+b2-2·4a·b+b2+2· y · 3) (-2x-1)2方法一方法二方法三 3) (-2x-1)2方法一解:原式=[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1方法二方法三一二一三 3) (-2x-1)2方法二解:原式=[(-2x)-1]2
= (-2x) 2 - 2· (-2x) ·1+1
=4x2+4x+1方法一方法三一二二三 3) (-2x-1)2方法三解:原式=[(-2x)+(-1)]2
=(-2x)2 + 2·(-2x) ·(-1) + (-1)2
=4x2+4x+1方法二方法一二三一三 3) (-2x-1)2方法一方法二方法三 原式=[(-2x)-1]2
=(-2x)2-2·(-2x)·1+1
=4x2+4x+1原式 =[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1 3) (-2x-1)2方法一方法三方法二原式 =[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1原式=[(-2x)+(-1)]2
=(-2x)2 + 2·(-2x) ·(-1) + (-1)2
=4x2+4x+1 3) (-2x-1)2方法二 原式=[(-2x)-1]2
=(-2x)2-2·(-2x)·1+1
=4x2+4x+1方法三原式=[(-2x)+(-1)]2
=(-2x)2 + 2·(-2x) ·(-1)
+ (-1)2
=4x2+4x+1方法一 3) (-2x-1)2方法一方法二方法三原式=[(-2x)+(-1)]2=(-2x)2+2·(-2x)·(-1)+(-1)2
=4x2+4x+1 原式=[(-2x)-1]2 =(-2x)2-2·(-2x)·1+1
=4x2+4x+1原式 =[-(2x+1)]2 =(2x+1)2
=(2x)2+2·2x·1+1=4x2+4x+1一二一三二三4) (b2+4a2)2解:原式 = (b2)2+2· b2 · (4a2) + (4a2)2
= b4 +8 a2 b2 + 16a4几点注意:1、项数:积的项数为三;2、符号:特别是(a-b)2= a2 - 2ab+b2;3、字母:不要漏写;4、字母指数:当公式中的a、b所代表的
单项式字母指数不是1时,乘方时要记
住字母指数需乘2。练习:下面各式的计算是否正确?如果不正确,应当怎样改正?(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3)(x -y)2 =x2+2xy +y2(4)(x+y)2 =x2 +xy +y2错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2-2xy +y2(x +y)2 =x2+2xy +y2(5)(2a?1)2=2a2?2a+1错 (2a?1)2=4a2?4a+1(6)(?a?1)2=?a2?2a?1.
错(?a?1)2=(?a)2?2?(?a )?1+12例2.运用完全平方公式计算:
1) 1022 2) 1992解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2
=2002-2×200×1+12
= 40000-400+1
= 39601练一练运用完全平方公式计算:
962 2) 1052
3)79.82 4) 80.32
小结注意完全平方公式和平方差公式不同:形式不同.结果不同:完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2. 有时需要进行变形,使变形后的式子符合应用完全平方公式
的条件,即为“两数和(或差)的平方”,然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积。
1.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积。
2.运用完全平方公式计算:
1) 1022 2) 1992再见!
