等腰三角形的判定[上学期]

课件18张PPT。等腰三角形的判定执教人：吴云芳(1)BAC复习1）在△ABC中∠B的对边是哪一条？

AC
∠C2）在△ABC中AB的对角是哪一个？
3）等腰三角形有哪些性质？ (1) 等腰三角形的两个底角相等。 (2)等腰三角形的顶角平分线、底边上 的中线、底边上的高互相重合。 (3)等腰三角形是轴对称图形，它的对称轴是顶角平分线所在的直线。 4）等腰三角形的两个底角相等，它的条件和结论是什么？条件：如果一个三角形是等腰三角形
结论：那么它的两个底角相等5）如果把这性质的条件和结论对换，那么新的条件和结论又是什么？ 条件：如果一个三角形有两个角相等
结论：那么这个三角形是等腰三角形在一个三角形中有两个角相等能否得出两条边相等，得出这个三角形是等腰三角形 ?操 作1）在纸上画△ABC，使∠B= ∠C（利用量角器）
2）再用量角器画出∠BAC的平分线AD，设AD与BC相交于D
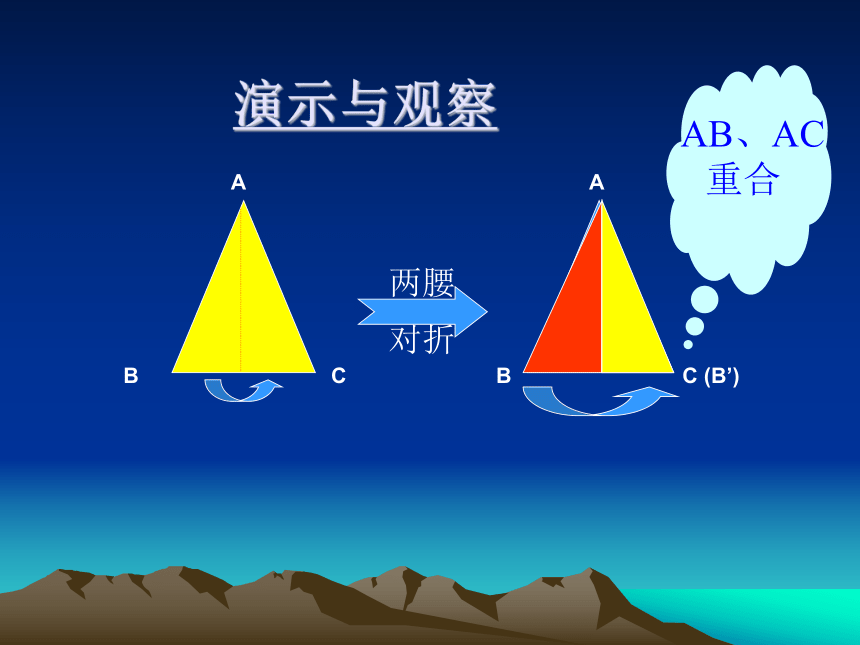
3）将△ABC纸片剪下，沿AD将△ABD翻折。问AB、AC重合吗？演示与观察
两腰对折 AB、AC
重合
ABCABC(B’) 等腰三角形的判定方法： 如果一个三角形有两个角相等，那么这两个角所对的边也相等，这个三角形是等腰三角形。（简写“等角对等边”） 符号语言：∵∠B=∠C
∴AC=AB
即△ABC是等腰三角形ACB例1：在△ABC中，∠A＝40°，∠B＝70° 问：（1）∠C等于几度？ （2）△ABC是什么三角形？ 分析： ∠A＝40°∠B＝70° ∠C=70°∠A+∠B+∠C＝180 °△ABC是等腰三角形∠C=∠BABC△ABC解：（1）∵∠A+∠B+∠C＝180°
（ 三角形内角和为180°）
∠A＝40°，∠B＝70°（已知）
∴∠C=180°－40°－70°＝70°
（2）∵∠B＝70° （已知）
∠C＝70 ° （已证）
∴∠B＝∠C
∴△ABC是等腰三角形（等角对等边）ABC例1：在△ABC中，∠A＝40°，∠B＝70° 问：（1）∠C等于几度？ （2）△ABC是什么三角形？ 例2：在△ABC中，∠B＝∠C＝65°，AB＝10cm 问：（1）△ABC是轴对称图形吗？如果是，说出 它的对称轴。（2）求AC的长。 分析：∠B＝∠C＝65° AB＝10cm ACBD△ABC是等腰三角形，
AB=ACAC=10cm
△ABC是轴对称图形对称轴：顶角平分线所在直线
底边上的中线所在直线
底边上的高所在直线ABCD解:（1）∵∠B＝∠C＝65°
（已知）
∴△ABC是等腰三角形
（等角对等边）
∴△ABC 是轴对称图形
（2）∵△ABC是等腰三角形
即：AB=AC，
AB＝10cm （已知）
∴AC＝10cm过点A作AD⊥BC，垂足为D， 则直线AD是△ABC的对称轴
例2：在△ABC中，∠B＝∠C＝65°，AB＝10cm 问：（1）△ABC是轴对称图形吗？如果是，说出它的对称轴。（2）求AC的长。例3：如图已知点E在BA的延长线上，∠1＝∠2，AD∥BC，问：△ABC是什么三角形？ B12CEAD解：∵ （已知）
∴∠1＝∠C
（两直线平行，内错角相等）
＝∠B
( )
∵∠1＝∠2 ( )
∴
∴△ABC是等腰三角形
( ) AD∥BC∠2两直线平行，同位角相等
已知∠C＝∠B等角对等边思考 在两个三角形中有两个角相等，
所对的两条边相等吗？举例说明BECAD12在△ABC和△DBE中
如果∠1＝∠2
则AB≠BD在两个三角形中，这个性质不一定成立。
BAOC×※※×根据图中所示的等量关系，写出已知条件，并求解OB=OC1）看图求解已知：在△ABC中，AB=AC，BO是∠ABC 的平分线，CO是∠ACB 的平分线，BO、CO相交于点O。
问：OB与OC相等吗？
拓展练习ABC1234O解：∵AB=AC（已知）
∴∠ABC=∠ACB（等边对等角）
∵BO是∠ABC 的平分线，CO是∠ACB 的平分线。（已知）
∴∠1=∠2，∠3=∠4（角平分线定义）
∴∠2=∠4
∴OB=OC （等角对等边）已知：在△ABC中，AB=AC，BO是∠ABC 的平分线，CO是∠ACB 的平分线，BO、CO相交于点O。
问：OB与OC相等吗？
2）有一个三角形纸片是等腰直角△ABC，其中 AB=AC， ∠A=90°
（1）能否把这个等腰直角△ABC分割成两个等腰直角三角形纸片？能的话，画出分割图形；（2）当∠A=108°时,又如何分割成两个等腰三角形纸片？（3）能否把（2）中的△ABC分割成三个等腰三角形纸片？能的话，画出分割图形。总结 1. 这节课学习了等腰三角形的判定方法：
（1）两条边相等的三角形是等腰三角形。
（2）如果一个三角形有两个角相等，那么这两个角所对的边也相等，这个三角形是等腰三角形。（简写“等角对等边”）
2.等腰三角形的判定方法及性质都是指在一个三角形中成立, 在两个三角形中，这个性质不一定成立。