等腰三角形的性质[上学期]

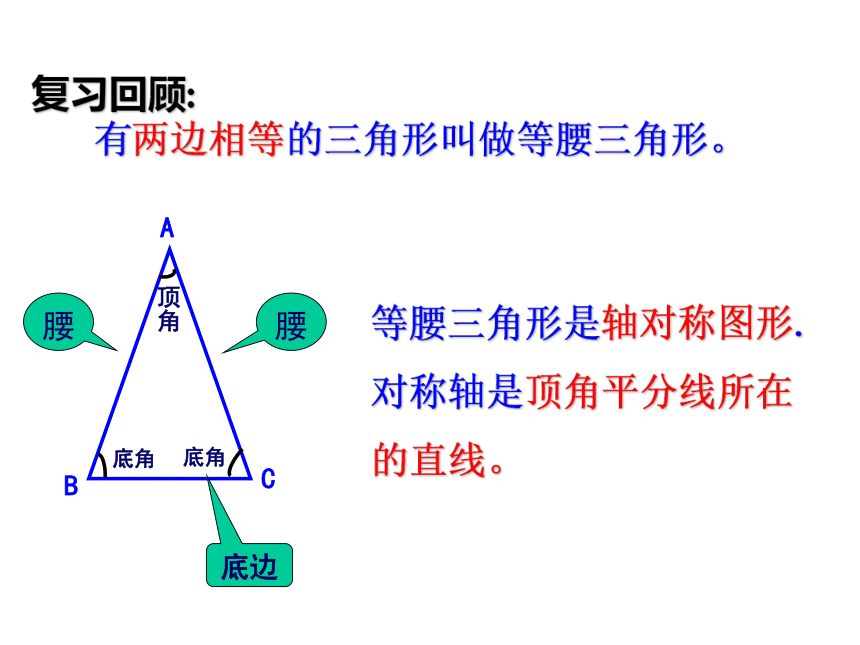
课件18张PPT。南马镇中厉云仙 有两边相等的三角形叫做等腰三角形。底边复习回顾:等腰三角形是轴对称图形.
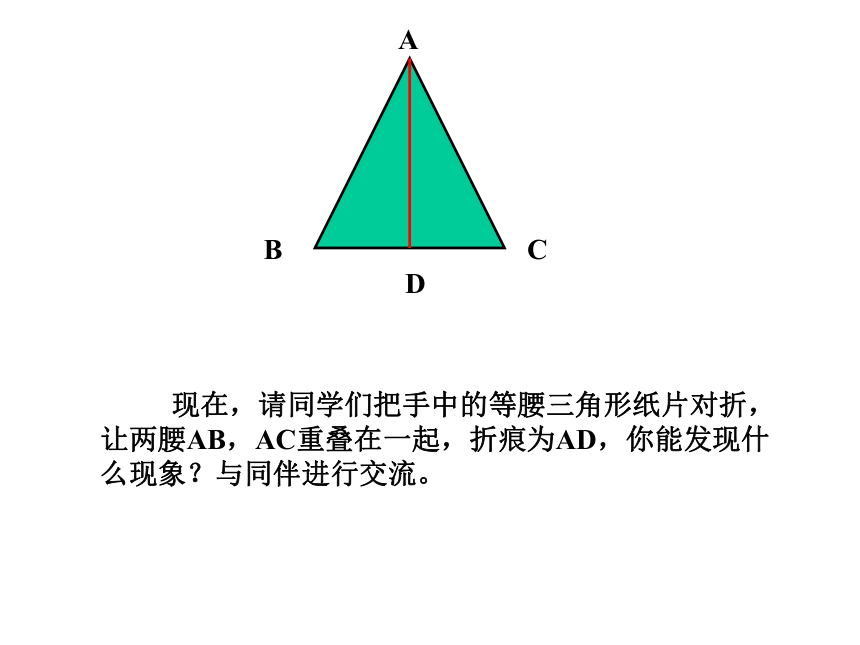
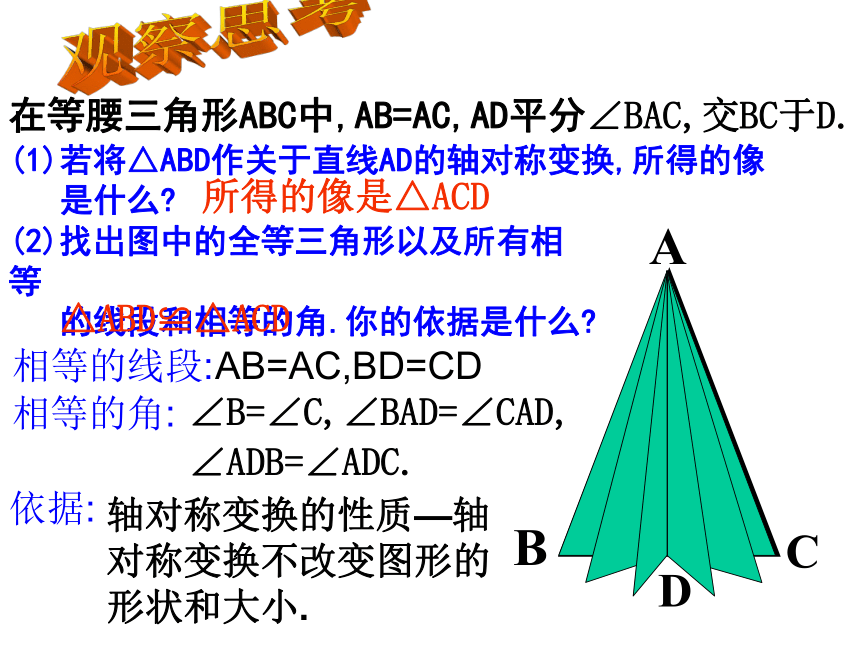
对称轴是顶角平分线所在的直线。 现在，请同学们把手中的等腰三角形纸片对折，让两腰AB，AC重叠在一起，折痕为AD，你能发现什么现象？与同伴进行交流。ABCD在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.(1)若将△ABD作关于直线AD的轴对称变换,所得的像
是什么?(2)找出图中的全等三角形以及所有相等
的线段和相等的角.你的依据是什么?所得的像是△ACD△ABD≌△ACD相等的线段:AB=AC,BD=CD相等的角:∠B=∠C,∠BAD=∠CAD,
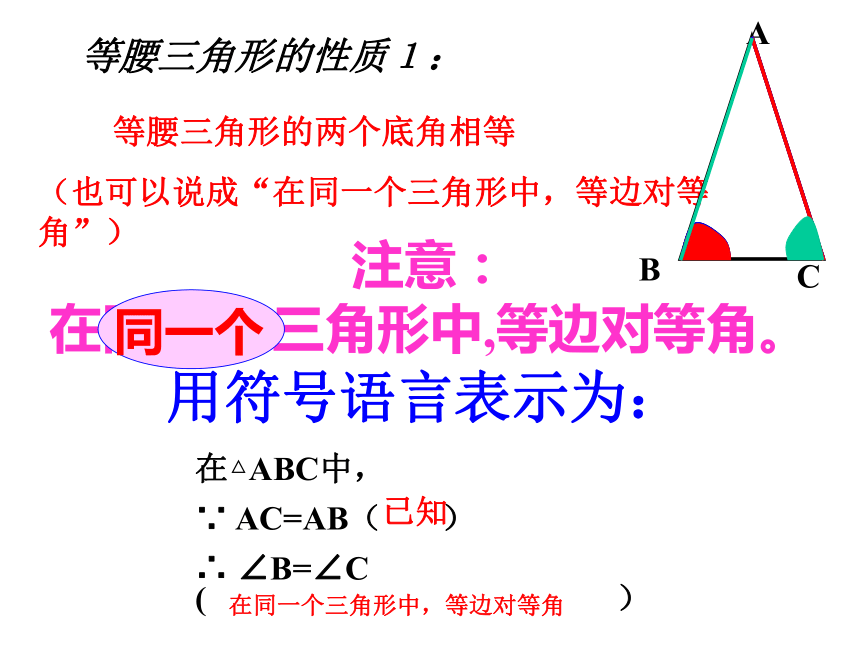
∠ADB=∠ADC.依据:轴对称变换的性质—轴对称变换不改变图形的形状和大小.观察思考等腰三角形的性质１： 等腰三角形的两个底角相等
（也可以说成“在同一个三角形中，等边对等角”）注意：
在同一个 三角形中,等边对等角。用符号语言表示为：在△ABC中，
∵ AC=AB（ ）
∴ ∠B=∠C ( ）已知在同一个三角形中，等边对等角等腰三角形的顶角平分线、底边上的中线和高互相重合.简称“等腰三角形三线合一”等腰三角形性质2∵AB=AC，∠1=∠2
∴________________＂等腰三角形三线合一＂的几何语言表述AD⊥BC，BD=CD∵AB=AC，AD⊥BC
∴________________∠1=∠2 ，BD=CD∵AB=AC，BD=CD
∴________________∠1=∠2 ， AD⊥BC例1、已知：在△ABC中，AB = AC，
∠A = 50°， 求∠B 和 ∠C的度数。ABC变式练习1:已知：在△ABC中，
AB = AC，∠A = 50°， 求∠B
和 ∠C的度数。BA变式练习2:已知：等腰三角形的一个
内角为 50 °， 求另两个角的度数.你行吗？（1）如图，在△ABC中，AB＝AC，
外角∠DCA＝100°，则∠B＝ 。
80°练习１（2）在△ABC中，AB＝AC，
若∠A＝40°则∠C＝ ；
若∠B＝72°，则∠A＝ 。70°36°90°20°（3）在△ABC中，AB＝AC，
∠BAC＝40°，M是BC的中点，
那么∠AMC＝ ，∠BAM＝ 。 ABCM（4）在△ABC中，AB＝AC， ∠ BAM＝ ∠CAN＝40°
那么∠B＝ 。若BM＝5，则CM＝ 。50°5如图，在等腰三角形ABC中，AB=AC，D为BC的中点，则点D到AB，AC的距离相等。请说明理由。练习二返回解法二：连接AD
∵ BD=CD,AB=AC（已知），
∴AD平分∠BAC(等腰三角形
三线合一）。
∵DE⊥AB，DF⊥AC（已知），
∴DE=DF（角平分线上的点到角两
边的距离相等。例2 已知线段a, h,用直尺和圆规作等腰三角形ABC,使底边BC=a, BC边上的高为h.ha作法:1.作线段BC=a.2.作BC的中垂线l,交BC于点D.3.在直线 l上截取DA=h,连接AB,AC.△ABC就是所求的等腰三角形.　　将一把三角尺和一个重锤如图放置，如果重锤线经过三角尺斜边的中点，那么就可以判定横梁是水平的，你知道为什么吗？ 请你思考生活链接1返回
拓展延伸
如图，在△ABC中，AB＝AC，直线AE交BC于点D，O是AE上一动点但不与A重合，且OB＝OC，试猜想AE与BC的关系，并说明你的猜想的理由。 猜想 AE垂直平分BC,理由如下：
在▲ABO和▲ACO中AB＝AC（已知）
OB＝OC（已知）
AO＝AO（公共边）
∴△ABO≌△ACO（SSS），
∴∠BAO＝∠CAO，
∴AE⊥BC，BD＝CD（等腰三角形三线合一）。请你说一说，通过短暂的数学之旅，你学到了什么知识?你还有那些困惑？必做作业
作业本 2.2A组NO1、2、3
B组NO1、2、3、4、
C组NO1、2、3、4、5、6
选做作业:
试探究等腰三角形两腰上的中线、高线大小关系。