利润问题[上学期]

课件9张PPT。欢迎各位老师听课指导一元二次方程的应用

-----利润问题
1.列一元二次方程解应用题的一般步骤是什么?


(1)审题 (2)设未知数 (3)列方程
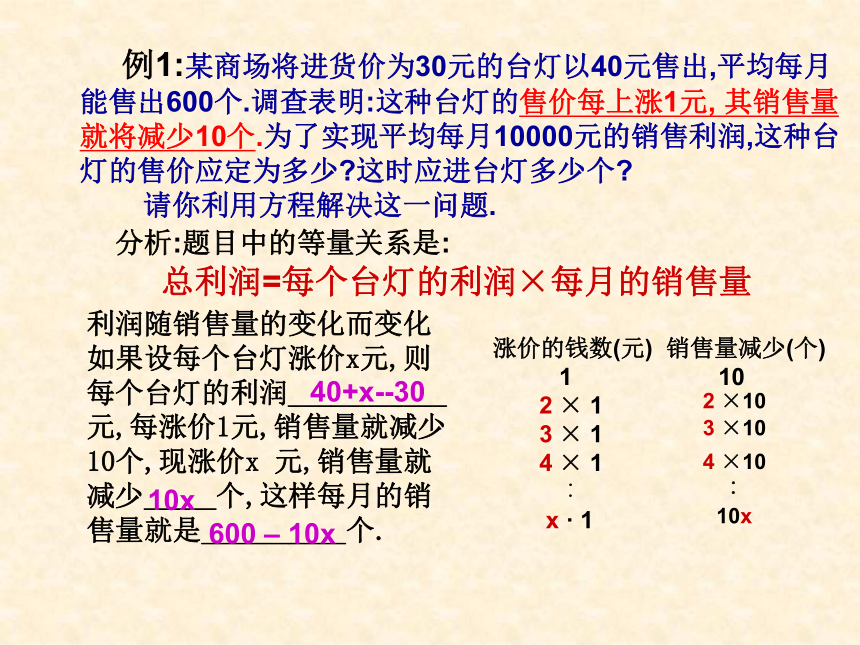
(4)解方程 (5)检验 (6)作答2.你知道利润问题中都有哪些等量关系吗? 利润=售价—进价 总利润=单件利润×数量 回顾与思考: 例1:某商场将进货价为30元的台灯以40元售出,平均每月
能售出600个.调查表明:这种台灯的售价每上涨1元, 其销售量
就将减少10个.为了实现平均每月10000元的销售利润,这种台
灯的售价应定为多少?这时应进台灯多少个?
请你利用方程解决这一问题.
分析:题目中的等量关系是:总利润=每个台灯的利润×每月的销售量利润随销售量的变化而变化如果设每个台灯涨价x元,则每个台灯的利润___________元,每涨价1元,销售量就减少10个,现涨价x 元,销售量就减少_____个,这样每月的销售量就是__________个.
10x600 – 10x涨价的钱数(元) 销售量减少(个)
1 10
2 × 1
3 × 1
4 × 1
︰
x · 1
2 ×103 ×104 ×10︰10x40+x--30解:设每个台灯涨价x元,则这种台灯的售价
应定为(40+x)元.根据题意可列方程
(40+x – 30)(600 –10x) =10000
2 2解这个方程得 x =10, x =40.
当x=10时,40+x=50,600 – 10x=500
当x=40时,40+x=80,600 – 10x=200
因此,每个台灯的售价定为50元时,应进500个台灯.每个台灯的售价定为80元时,应进200个台灯.
整理得 x – 50x + 400 = 01 例2:新华商场销售某种冰箱,每台进货价为2500元.
市场调研表明:当销售价为2900元时,平均每天能售出8
台;而当销售价每降低50元时,平均每天就能多售出4台.
商场要想使这种冰箱的销售利润平均每天达到5000元,
每台冰箱的定价应为多少元?
分析:题目的主要等量关系是:
每台冰箱的利润×每天销售冰箱的数量=总利润完成下列表格:82900－25008+4×50002900 －x－2500解:设每台冰箱降价x元,则每台冰箱的售 价为(2900--x)元,根据题意,得:
(2900 –x – 2500)(8+4× )=5000
1
解这个方程得x1 = x =150
2900–x=2900 –150=2750
所以,每台冰箱的定价应为2750元.整理得 x – 300x+22500=022小结:
列方程解应用题的三个主要环节3.正确求解方程并检验解的合理性.2.把握问题中的等量关系.1.整体地,系统地审清问题.谢谢
再见