苏教版小数六上第一单元长方体和正方体真题练习(含答案)
文档属性
| 名称 | 苏教版小数六上第一单元长方体和正方体真题练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 88.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-05 15:42:09 | ||
图片预览



文档简介
苏教版小数六上第一单元长方体和正方体真题练习1
一、选择题(满分16分)
1.(2021·江苏盐城·六年级期末)下面图形中,( )图沿虚线折叠后不能围成正方体。
A. B.
C. D.
2.(2020·江苏·六年级期中)正方体的棱长扩大到原来的2倍,那么体积扩大到原来的( )倍。
A.2 B.4 C.8
3.(2022·江苏连云港·六年级期末)一个文具盒的体积大约180( )。
A.立方毫米 B.立方厘米 C.立方分米 D.立方米
4.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学六年级期末)一个长方体木桶,从外面量长是6分米,宽是5分米,高4分米。它的容量可能是( )。
A.120升 B.100升 C.130升 D.30升
5.(2022·江苏无锡·六年级期末)把一个长10cm、宽8cm、高6cm的长方体,切成两个相等的长方体,它们的表面积之和比原来最多增加( )平方厘米。
A.480 B.160 C.96 D.80
6.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学六年级期末)一个正方体的棱长总和是48分米,它的表面积是( )。
A.64平方分米 B.96平方分米 C.144平方分米 D.72平方分米
7.(2021·江苏盐城·六年级期末)一个长方体正好能切成3个棱长是4厘米的正方体(如图),3个正方体的表面积之和比原来长方体增加了( )平方厘米。
A.16 B.32 C.480 D.64
8.(2021·江苏盐城·六年级期末)把体积是1立方米的正方体木块,平均切成棱长是1分米的小正方体木块,一共可以切成( )个。
A.10 B.100 C.1000 D.10000
二、填空题(满分16分)
9.(2022·江苏扬州·六年级期末)在下列的括号里填上适当的数。
45分=( )时 12毫升=( )立方分米
10.(2021·江苏淮安·六年级期末)用铁丝焊接一个长10厘米、宽8厘米、高5厘米的长方体框架,至少需要铁丝( )厘米。如果用白纸贴满长方体的各个面,至少要用白纸( )平方厘米;这个长方体的体积是( )立方厘米。
11.(2019·江苏·六年级单元测试)一个长方体的长、宽、高都扩大到原来的2倍,表面积就扩大到原来的( )倍,体积扩大到原来的( )倍。
12.(2021·江苏·六年级单元测试)一个正方体棱长的总和是60厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
13.(2021·江苏南京·小升初真题)棱长是4厘米的正方体的表面积是( )平方厘米,体积是( )立方厘米,可以截成棱长是2厘米的正方体( )个。
14.(2022·江苏徐州·六年级期末)把长12米的长方体材料(如图),平均锯成3段后,表面积比原来增加2.4平方米,原来这根木料的体积是( )立方米。
15.(2021·江苏·兴化市乐吾实验学校六年级阶段练习)一个长方体的纸箱长是7分米,宽是6分米,高是4.5分米。最大的面的长是( )分米,宽是( )分米,一个这样的面的面积是( )平方分米;最小的面的面积是( )平方分米。
16.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学六年级期末)一根5米长的长方体木料,木工师傅把它锯成3段,表面积增加了24平方米,这根木料的横截面是( )平方米。
三、判断题(满分8分)
17.(2020·江苏·六年级课时练习)两个体积一样的大盒子,它们的容积一定同样大。( )
18.(2022·江苏·六年级)把一个棱长为4厘米的正方体切割成两个完全一样的长方体,每个长方体的体积是32立方厘米,表面积是48平方厘米。( )
19.(2021·江苏·六年级期末)一个正方体的棱长总和是36厘米,它的体积和表面积相等。( )
20.(2021·江苏无锡·六年级期中)一个棱长为6cm的正方体,它的表面积和体积相等。( )
四、图形计算题(满分6分)
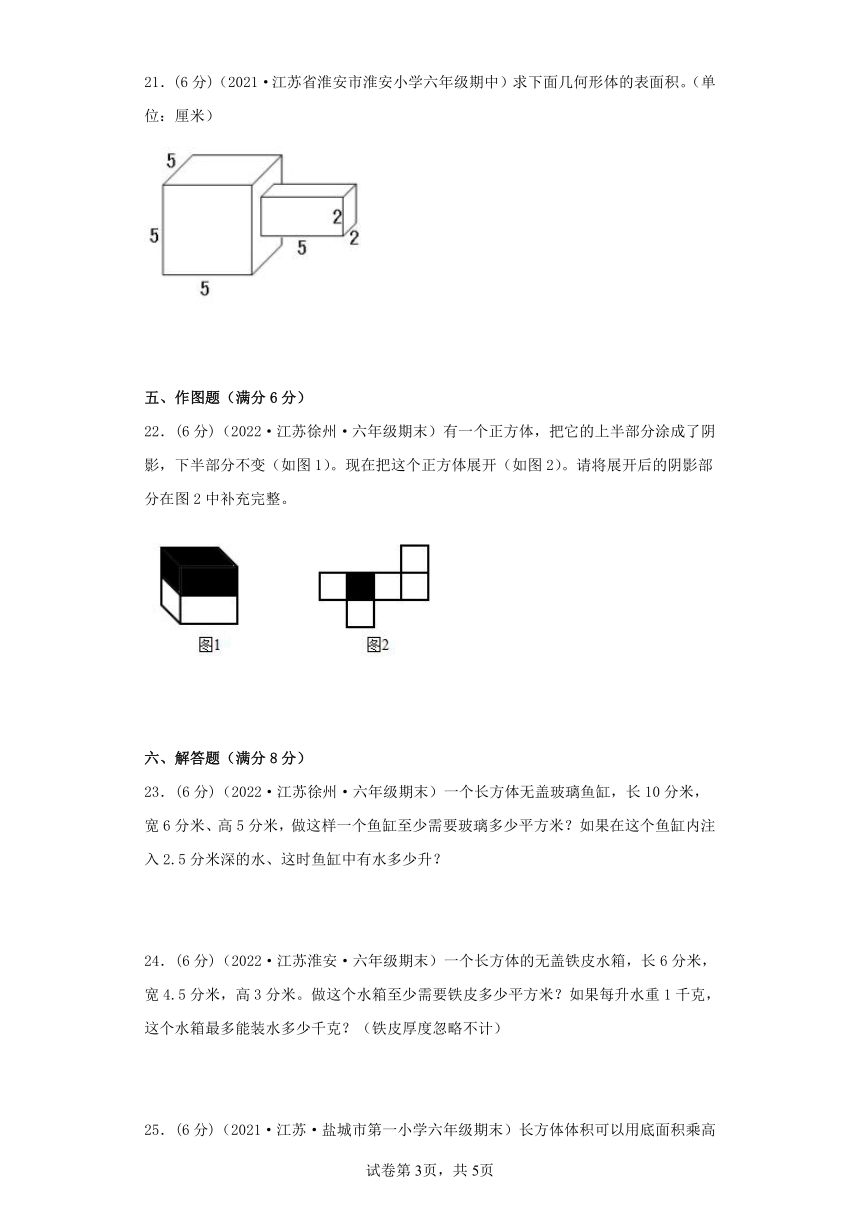
21.(6分)(2021·江苏省淮安市淮安小学六年级期中)求下面几何形体的表面积。(单位:厘米)
五、作图题(满分6分)
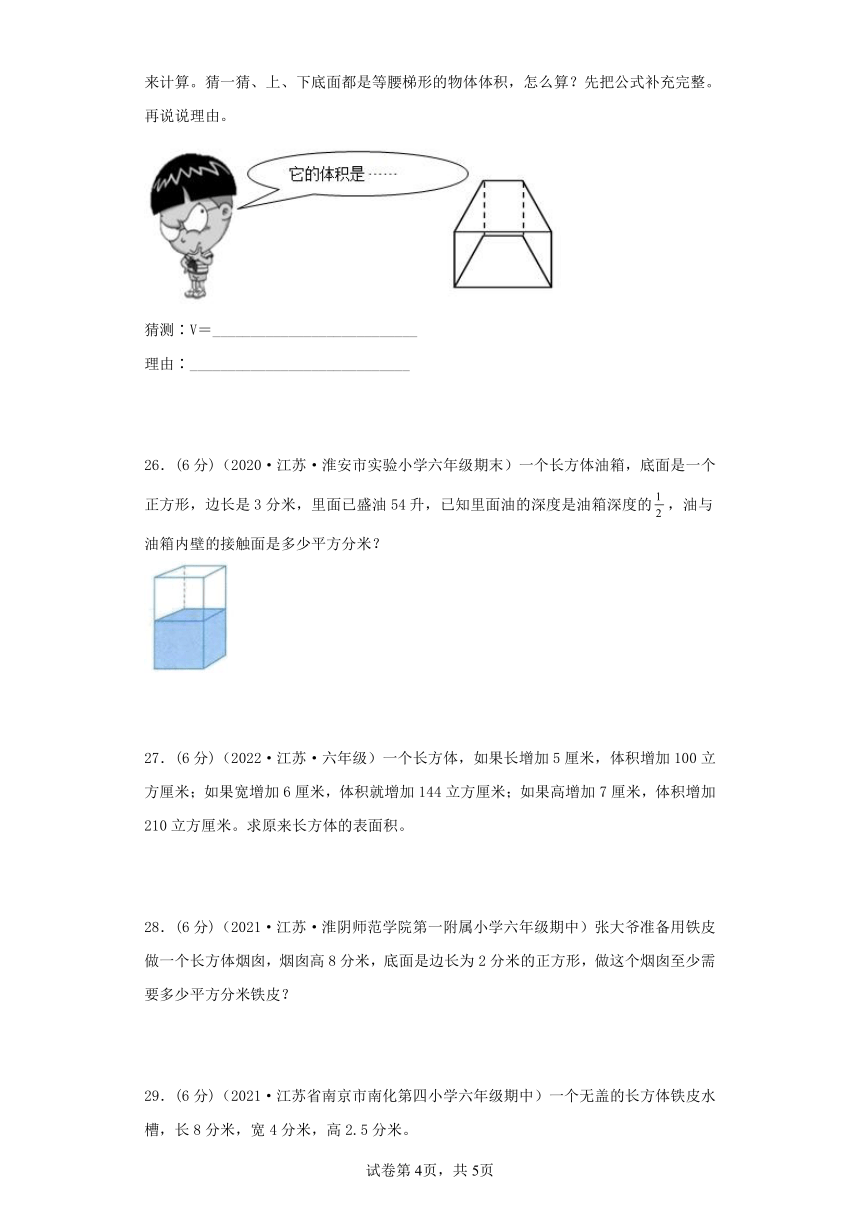
22.(6分)(2022·江苏徐州·六年级期末)有一个正方体,把它的上半部分涂成了阴影,下半部分不变(如图1)。现在把这个正方体展开(如图2)。请将展开后的阴影部分在图2中补充完整。
六、解答题(满分8分)
23.(6分)(2022·江苏徐州·六年级期末)一个长方体无盖玻璃鱼缸,长10分米,宽6分米、高5分米,做这样一个鱼缸至少需要玻璃多少平方米?如果在这个鱼缸内注入2.5分米深的水、这时鱼缸中有水多少升?
24.(6分)(2022·江苏淮安·六年级期末)一个长方体的无盖铁皮水箱,长6分米,宽4.5分米,高3分米。做这个水箱至少需要铁皮多少平方米?如果每升水重1千克,这个水箱最多能装水多少千克?(铁皮厚度忽略不计)
25.(6分)(2021·江苏·盐城市第一小学六年级期末)长方体体积可以用底面积乘高来计算。猜一猜、上、下底面都是等腰梯形的物体体积,怎么算?先把公式补充完整。再说说理由。
猜测∶V=___________________________
理由∶_____________________________
26.(6分)(2020·江苏·淮安市实验小学六年级期末)一个长方体油箱,底面是一个正方形,边长是3分米,里面已盛油54升,已知里面油的深度是油箱深度的,油与油箱内壁的接触面是多少平方分米?
27.(6分)(2022·江苏·六年级)一个长方体,如果长增加5厘米,体积增加100立方厘米;如果宽增加6厘米,体积就增加144立方厘米;如果高增加7厘米,体积增加210立方厘米。求原来长方体的表面积。
28.(6分)(2021·江苏·淮阴师范学院第一附属小学六年级期中)张大爷准备用铁皮做一个长方体烟囱,烟囱高8分米,底面是边长为2分米的正方形,做这个烟囱至少需要多少平方分米铁皮?
29.(6分)(2021·江苏省南京市南化第四小学六年级期中)一个无盖的长方体铁皮水槽,长8分米,宽4分米,高2.5分米。
(1)做这个水槽需要多少平方分米的铁皮?
(2)这个水槽装满水,水重多少千克?(1升水重1千克)
30.(6分)(2022·江苏泰州·六年级期末)光明小学准备修建一个长6米、宽3米、深50厘米的沙坑。
(1)如果要在沙坑的四周和底面抹上水泥,抹水泥的面积是多少平方米?
(2)如果要在沙坑里填满黄沙,准备黄沙19吨,够不够?(每立方米黄沙重2.4吨)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【解析】
【分析】
正方体展开图有四种类型,即“一四一”,“二二二“、“三三”、“一三二”,据此解答。
【详解】
A.属于正方体展开图“二二二”类型;
B.不属于正方体展开图;
C.属于正方体展开图“一四一”类型;
D.属于正方体展开图“一三二”类型。
答案:B
【点评】
主要考查正方体展开图,熟练掌握正方体展开图的特征,也可以动手实践操作下。
2.C
【解析】
【分析】
根据正方体的体积=棱长×棱长×棱长,以及积的变化规律:因数乘几或除以几(0除外),积就乘几或除以几;据此解答。
【详解】
2×2×2
=4×2
=8
正方体的棱长扩大到原来的2倍,那么体积扩大到原来的8倍。
答案:C
【点评】
掌握正方体的体积计算公式以及积的变化规律是解题的关键。
3.B
【解析】
【分析】
根据生活经验,对体积单位和数据的大小认识,可知计量一个文具盒的体积用“立方厘米”做单位。
【详解】
由分析可知;一个文具盒的体积大约180立方厘米。
答案:B
【点评】
此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
4.B
【解析】
【分析】
首先根据长方体的体积公式:v=abh,把数据代入公式求出这个木桶的体积,由于木桶的木板有一定的厚度,所以它的容积要小于它的体积,据此解答。
【详解】
6×5×4=120(立方分米)
120立方分米=120升
木桶的容积<120升,100升最符合题意。
答案:B
【点评】
此题主要考查长方体的体积公式的灵活运用,关键是熟记公式。
5.B
【解析】
【分析】
将长方体切成两个,如果切面的长和宽是最大值,那么表面积增加的是最多的,由此可知,长10cm,宽8cm,增加的是2个面的面积,用10×8×2即可解答。
【详解】
10×8×2
=80×2
=160(平方厘米)
答案:B
【点评】
此题主要考查学生对长方体表面积的理解与认识。
6.B
【解析】
【分析】
由正方体的特征可知:正方体共有12条棱,且每条棱长都相等,棱长总和是48分米,则可以求出每条棱的长度,进而利用正方体的表面积公式就可以求出其表面积。
【详解】
棱长:48÷12=4(分米)
正方体的表面积:
4×4×6
=16×6,
=96(平方分米)
答案:B
【点评】
解答此题的主要依据是:正方体共有12条棱长,且每条棱长都相等以及正方体的表面积公式。
7.D
【解析】
【分析】
通过观察图形可知,一个长方体正好能切成3个棱长是4厘米的正方体,3个正方体的表面积之和比原来长方体增加了4个切面的面积,根据正方形的面积公式:S=a2,把数据代入公式解答。
【详解】
4×4×4
=16×4
=64(平方厘米)
答案:D
【点评】
此题考查的目的是理解掌握长方体、正方体表面积的意义,关键是明确:一个长方体正好能切成3个棱长是4厘米的正方体,3个正方体的表面积之和比原来长方体增加了4个切面的面积。
8.C
【解析】
【分析】
根据1立方米与1立方分米的进率是1000即可判断。
【详解】
因为1立方米=1000立方分米,
也就相当于1立方米里面有1000个1立方分米,
所以体积是1立方米的正方体木块,可以切割成1000个1立方分米的小正方体木块;
答案:C
【点评】
此题也可以利用画图操作,进行观察,根据1米=10分米,每个棱上可以割成10个,一共可割成:10×10×10=1000个,然后选出答案即可。
9.##0.75 ##0.012
【解析】
【分析】
低级单位化高级单位,除以单位之间的进率。1时=60分,1立方分米=1升=1000毫升。
【详解】
45÷60=,则45分=时;
12÷1000=,则12毫升=立方分米。
【点评】
考查单位的换算。要熟练掌握单位之间的进率和换算方法。
10.92 340 400
【解析】
【分析】
根据长方体的棱长总和=(长+宽+高)×4,代入数据,求出这个长方体的棱长总和;再根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,求出至少要用白纸的面积;再根据长方体体积公式:长×宽×高,代入数据,即可解答。
【详解】
棱长总和:
(10+8+5)×4
=(18+5)×4
=23×4
=92(厘米)
表面积:
(10×8+10×5+8×5)×2
=(80+50+40)×2
=(130+40)×2
=170×2
=340(平方厘米)
10×8×5
=80×5
=400(立方厘米)
【点评】
根据长方体的棱长总和公式、表面积公式、体积公式进行解答,关键是熟记公式。
11.4 8
【解析】
【分析】
根据长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,设出原来的长、宽、高,利用长方体的表面积公式表示出其表面积,再用现在的长、宽、高,得出现在的表面积,用现在的表面积除以原来的表面积,就是表面积扩大的倍数,同理得出体积扩大的倍数。
【详解】
令原来的长、宽、高分别为a、b、h,
则原来的表面积:(ab+ah+bh)×2
现在的表面积:(2a×2b+2a×2h+2b×2h)×2
=(4ab+4ah+4bh)×2
=(ab+ah+bh)×8
现在的表面积是原来的:[(ab+ah+bh)×8]÷[(ab+ah+bh)×2]=4
原来的体积:abh
现在的体积:2a×2b×2h=8abh
现在的体积是原来的:8abh÷abh=8
所以一个长方体的长、宽、高都扩大到原来的2倍,则表面积扩大到原来的4倍,体积扩大到原来的8倍。
【点评】
此题主要考查长方体的表面积公式、体积公式的灵活运用,以及因数与积的变化规律的应用。
12.150 125
【解析】
【分析】
由题意得正方体的棱长=总和÷12,再根据正方体的表面积=6a2计算出表面积,根据计算体积。
【详解】
60÷12=5(厘米)
6×5×5=150(平方厘米)
5×5×5=125(立方厘米)
【点评】
根据正方体的棱长=总和÷12求出正方体的棱长是解题的关键。
13.96 64 8
【解析】
【分析】
①根据正方体的表面积和体积公式即可求得其表面积和体积;
②抓住正方体分割前后的体积不变,即可得出小正方体的个数。
【详解】
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)
2×2×2=8(立方厘米)
64÷8=8(个)
则棱长是4厘米的正方体的表面积是96平方厘米,体积是64立方厘米,可以截成棱长是2厘米的正方体8个。
【点评】
此题考查了正方体表面积和体积公式的灵活应用,以及正方体分割的方法。
14.7.2
【解析】
【分析】
根据题意可知,把长12米的长方体材料,平均锯成3段后,表面积比原来增加2.4平方米,表面积增加的是4个截面的面积,据此可以求出每个截面的面积,然后根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】
2.4÷4×12
=0.6×12
=7.2(立方米)
原来这根木料的体积是7.2立方米。
【点评】
此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是求出长方体的底面积。
15.7 6 42 27
【解析】
【分析】
根据长方体的特征,这个长方体的6个面都是长方形,相对的面的面积相等。由题意可知,这个长方体纸盒的最大面是底面,长是7分米,宽是6分米;最小面是左右面,长是6分米,宽是4.5分米;根据长方形的面积公式:S=ab,分别求出它们的面积。
【详解】
最大面的长是7分米,宽是6分米,面积是:7×6=42(平方分米);
最小面的长是6分米,宽是4.5分米,面积是:6×4.5=27(平方分米)。
【点评】
此题主要考查长方体表面积的计算,需要根据长方形的面积公式解答。
16.6
【解析】
【分析】
锯成3段后,表面积增加了4个横截面的面积,因为表面积是增加了24平方米,由此即可求出横截面的面积是24÷4=6平方米,据此解答即可。
【详解】
根据分析,这根木料的横截面是:
24÷4=6(平方米)
【点评】
抓住长方体的切割特点和增加的表面积求出长方体的横截面的面积是解决此题的关键。
17.×
【解析】
【分析】
容积是指物体所容纳物体的体积,两个体积一样大的盒子,盒皮的厚度不一样,所容纳物体的体积就不一样,盒皮厚的容纳的体积少些,盒皮薄的容纳的体积多些,如果厚度一样,容积就一样大,据此解答即可。
【详解】
两个体积一样大的盒子,它们的容积一定同样大的说法是错误的,应该是容积不一定同样大。
答案:×
【点评】
此题考查容积的意义,解决此题的关键是容积的定义,注重盒皮的厚度。
18.×
【解析】
【分析】
由“一个棱长为4厘米的正方体”可以求出正方体的1个面的面积,则切出的每个小长方体的表面积都等于原正方体的表面积的一半与一个正方体的面的面积之和,据此即可解答。
【详解】
4×4×6÷2+4×4
=48+16
=64(平方厘米)
答案:×
【点评】
此题考查的是长方体表面积和体积计算,解答此题的关键是明确每个小长方体的表面积都包括哪几个部分。
19.×
【解析】
【分析】
正方体的棱长=棱长总和÷12,据此求出正方体的棱长,正方体的体积=棱长×棱长×棱长,正方体的表面积=棱长×棱长×6,据此解答。
【详解】
36÷12=3(厘米)
体积:3×3×3=27(立方厘米),表面积:3×3×6=54(平方厘米)
体积和表面积不是同一种量,无法比较,原题说法错误。
答案:×
【点评】
物体的体积和表面积不是同一种量,无法进行比较。
20.×
【解析】
【分析】
物体的表面或封闭图形的大小,叫做它们的面积。体积是指物体所占空间的大小。表面积和体积意义不同,无法比较,据此分析。
【详解】
一个棱长为6cm的正方体,它的表面积和体积无法比较,所以原题说法错误。
答案:×
【点评】
正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。
21.190平方厘米
【解析】
【分析】
观察图形可知,棱长5厘米的正方体的表面积,与长是5厘米,宽是2厘米的长方体的侧面积之和,四个面相等,根据正方体表面积公式:棱长×棱长×6,长方体侧面积公式:长×宽×4,代入数据,即可解答。
【详解】
5×5×6+5×2×4
=25×6+10×4
=150+40
=190(平方厘米)
22.见详解
【解析】
【分析】
根据图可知,这个完全涂上黑色的小正方形的四周有4个小正方形被涂上一半,根据正方体展开图的特征,即可知道图2黑色区域的小正方形,它的左边和右边的小正方形各涂了一半阴影,即竖直涂上一半的阴影,这两部分阴影和2黑色区域阴影部分挨着;它下面涂色部分是横着的阴影,也和它挨着;第4个小正方形是展开图的最右上角的小正方形,它的涂色区域是水平的一半,再上面。
【详解】
由分析可知:
【点评】
主要考查正方体展开图,可以动手实际操作一下。
23.2.2平方米;150升
【解析】
【分析】
由于鱼缸是无盖的,根据长方体5个面的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解,再根据1平方米=100平方分米,转换单位即可;由于注入2.5分米深的水,则此时水形成的形状是一个长10分米,宽6分米,高2.5分米的长方体,根据长方体的体积公式:长×宽×高,把数代入公式即可求解,再根据1升=1立方分米,由此转换单位。
【详解】
10×6+(10×5+6×5)×2
=60+(50+30)×2
=60+80×2
=60+160
=220(平方分米)
220平方分米=2.2平方米。
10×6×2.5
=60×2.5
=150(立方分米)
150立方分米=150升
答:做这样一个鱼缸需要玻璃2.2平方米;这时鱼缸中有水150升。
【点评】
主要考查长方体的表面积和体积公式,熟练掌握它们的公式并灵活运用,要注意转换单位。
24.0.9平方米,81千克
【解析】
【分析】
铁皮的面积=(长×高+宽×高)×2+长×宽,代入数据计算即可;水的体积=长×宽×高,再乘每升水的质量即可。
【详解】
(6×3+4.5×3)×2+6×4.5
=(18+13.5)×2+27
=63+27
=90(平方分米)
=0.9(平方米);
6×4.5×3
=27×3
=81(立方分米)
=81(升)
81×1=81(千克)
答:做这个水箱至少需要铁皮0.9平方米,这个水箱最多能装水81千克。
【点评】
此题考查了长方体表面积和体积的综合应用,需牢记公式认真计算,注意单位换算。
25.见详解
【解析】
【分析】
长方体的体积=长×宽×高,又长×宽是长方体的底面积,由此推知长方体的体积=底面积×高,进而推测出上、下底面都是等腰梯形的物体体积公式;据此解答。
【详解】
猜测∶V=Sh
理由∶先求出梯形的面积S=(上底+下底)×高÷2,四棱柱的体积V则为梯形的面积S×棱柱的高h。
【点评】
通过对长方体体积公式的理解,合理推测即可。
26.81平方分米
【解析】
【分析】
先根据1立方分米=1升换算出油的体积是多少立方分米,然后用油的体积除以长方体油箱的底面积,即可得到油的深度,再根据长方体表面积计算公式求出油与油箱内壁的接触面积。
【详解】
54升=54立方分米
油的深度:
54÷(3×3)
=54÷9
=6(分米)
油与油箱内壁的接触面积:
3×6×4+3×3
=72+9
=81(平方分米)
答:油与油箱内壁的接触面积是81平方分米。
【点评】
此题主要考查长方体的体积的计算方法的灵活应用.注意体积单位和容积单位的换算。
27.148平方厘米
【解析】
【分析】
当长增加5厘米,则宽和高不变,此时增加部分的体积:5×宽×高=100,由此即可求出宽×高=20平方厘米;宽增加6厘米,则长和高不变,增加部分的体积:长×高×6=144,则长×高=24平方厘米;高增加7厘米,则长和宽不变,增加部分的体积:长×宽×7=210,则长×宽=30平方厘米,之后根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,把数代入公式即可求解。
【详解】
宽×高:100÷5=20(平方厘米)
长×高:144÷6=24(平方厘米)
长×宽:210÷7=30(平方厘米)
表面积:(20+24+30)×2
=74×2
=148(平方厘米)
答:原来长方体的表面积是148平方厘米。
【点评】
此题关键是理解长增加宽和高不变,宽增加长和高不变,高增加长和宽不变。根据长方体的表面积公式解答即可。
28.64平方分米
【解析】
【分析】
由于长方体烟囱有4个面,没有上下两个面,即根据长方体的表面积公式:(长×高+宽×高)×2,把数代入公式即可。
【详解】
(8×2+8×2)×2
=(16+16)×2
=32×2
=64(平方分米)
答:做这个烟囱至少需要64平方分米铁皮。
【点评】
主要考查长方体的表面积公式,要注意联系生活实际看这个长方体有几个面。
29.(1)92平方分米;
(2)80千克
【解析】
【分析】
(1)由题意可知,做这个水槽需要前后、左右和下共5个面,则需要“长×高×2+宽×高×2+长×宽”平方分米的铁皮;
(2)根据 “长方体的容积=长×宽×高”求出水槽中水的体积,再乘1升水的质量即可。
【详解】
(1)8×4+8×2.5×2+4×2.5×2
=32+40+20
=92(平方分米)
答:做这个水槽需要92平方分米的铁皮。
(2)8×4×2.5×1
=32×2.5
=80(千克)
答:水重80千克。
【点评】
熟练掌握长方体表面积和体积的计算方法是解答的关键。
30.(1)27平方米;(2)不够
【解析】
【分析】
(1)根据题意,求出这个沙坑的底面积加上四个侧面积,根据长方体的表面积公式:长×宽+(长×高+宽×高)×2,代入数据,即可解答;
(2)根据长方体的体积公式:长×宽×高,用体积×2.4,再和19吨比较,大于19吨,就不够,小于19吨,就够。
【详解】
(1)50厘米=0.5米
6×3+(6×0.5+3×0.5)×2
=18+(3+1.5)×2
=18+4.5×2
=18+9
=27(平方米)
答:抹水泥的面积是27平方米。
(2)6×3×0.5×2.4
=18×0.5×2.4
=9×2.4
=21.6(吨)
21.6>19
准备19吨黄沙不够。
答:不够。
【点评】
考查长方体表面积公式、体积公式的应用,注意单位名数的统一。
答案第1页,共2页
答案第1页,共2页
一、选择题(满分16分)
1.(2021·江苏盐城·六年级期末)下面图形中,( )图沿虚线折叠后不能围成正方体。
A. B.
C. D.
2.(2020·江苏·六年级期中)正方体的棱长扩大到原来的2倍,那么体积扩大到原来的( )倍。
A.2 B.4 C.8
3.(2022·江苏连云港·六年级期末)一个文具盒的体积大约180( )。
A.立方毫米 B.立方厘米 C.立方分米 D.立方米
4.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学六年级期末)一个长方体木桶,从外面量长是6分米,宽是5分米,高4分米。它的容量可能是( )。
A.120升 B.100升 C.130升 D.30升
5.(2022·江苏无锡·六年级期末)把一个长10cm、宽8cm、高6cm的长方体,切成两个相等的长方体,它们的表面积之和比原来最多增加( )平方厘米。
A.480 B.160 C.96 D.80
6.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学六年级期末)一个正方体的棱长总和是48分米,它的表面积是( )。
A.64平方分米 B.96平方分米 C.144平方分米 D.72平方分米
7.(2021·江苏盐城·六年级期末)一个长方体正好能切成3个棱长是4厘米的正方体(如图),3个正方体的表面积之和比原来长方体增加了( )平方厘米。
A.16 B.32 C.480 D.64
8.(2021·江苏盐城·六年级期末)把体积是1立方米的正方体木块,平均切成棱长是1分米的小正方体木块,一共可以切成( )个。
A.10 B.100 C.1000 D.10000
二、填空题(满分16分)
9.(2022·江苏扬州·六年级期末)在下列的括号里填上适当的数。
45分=( )时 12毫升=( )立方分米
10.(2021·江苏淮安·六年级期末)用铁丝焊接一个长10厘米、宽8厘米、高5厘米的长方体框架,至少需要铁丝( )厘米。如果用白纸贴满长方体的各个面,至少要用白纸( )平方厘米;这个长方体的体积是( )立方厘米。
11.(2019·江苏·六年级单元测试)一个长方体的长、宽、高都扩大到原来的2倍,表面积就扩大到原来的( )倍,体积扩大到原来的( )倍。
12.(2021·江苏·六年级单元测试)一个正方体棱长的总和是60厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
13.(2021·江苏南京·小升初真题)棱长是4厘米的正方体的表面积是( )平方厘米,体积是( )立方厘米,可以截成棱长是2厘米的正方体( )个。
14.(2022·江苏徐州·六年级期末)把长12米的长方体材料(如图),平均锯成3段后,表面积比原来增加2.4平方米,原来这根木料的体积是( )立方米。
15.(2021·江苏·兴化市乐吾实验学校六年级阶段练习)一个长方体的纸箱长是7分米,宽是6分米,高是4.5分米。最大的面的长是( )分米,宽是( )分米,一个这样的面的面积是( )平方分米;最小的面的面积是( )平方分米。
16.(2022·江苏省淮安市淮阴区淮阴师范学院第二附属小学六年级期末)一根5米长的长方体木料,木工师傅把它锯成3段,表面积增加了24平方米,这根木料的横截面是( )平方米。
三、判断题(满分8分)
17.(2020·江苏·六年级课时练习)两个体积一样的大盒子,它们的容积一定同样大。( )
18.(2022·江苏·六年级)把一个棱长为4厘米的正方体切割成两个完全一样的长方体,每个长方体的体积是32立方厘米,表面积是48平方厘米。( )
19.(2021·江苏·六年级期末)一个正方体的棱长总和是36厘米,它的体积和表面积相等。( )
20.(2021·江苏无锡·六年级期中)一个棱长为6cm的正方体,它的表面积和体积相等。( )
四、图形计算题(满分6分)
21.(6分)(2021·江苏省淮安市淮安小学六年级期中)求下面几何形体的表面积。(单位:厘米)
五、作图题(满分6分)
22.(6分)(2022·江苏徐州·六年级期末)有一个正方体,把它的上半部分涂成了阴影,下半部分不变(如图1)。现在把这个正方体展开(如图2)。请将展开后的阴影部分在图2中补充完整。
六、解答题(满分8分)
23.(6分)(2022·江苏徐州·六年级期末)一个长方体无盖玻璃鱼缸,长10分米,宽6分米、高5分米,做这样一个鱼缸至少需要玻璃多少平方米?如果在这个鱼缸内注入2.5分米深的水、这时鱼缸中有水多少升?
24.(6分)(2022·江苏淮安·六年级期末)一个长方体的无盖铁皮水箱,长6分米,宽4.5分米,高3分米。做这个水箱至少需要铁皮多少平方米?如果每升水重1千克,这个水箱最多能装水多少千克?(铁皮厚度忽略不计)
25.(6分)(2021·江苏·盐城市第一小学六年级期末)长方体体积可以用底面积乘高来计算。猜一猜、上、下底面都是等腰梯形的物体体积,怎么算?先把公式补充完整。再说说理由。
猜测∶V=___________________________
理由∶_____________________________
26.(6分)(2020·江苏·淮安市实验小学六年级期末)一个长方体油箱,底面是一个正方形,边长是3分米,里面已盛油54升,已知里面油的深度是油箱深度的,油与油箱内壁的接触面是多少平方分米?
27.(6分)(2022·江苏·六年级)一个长方体,如果长增加5厘米,体积增加100立方厘米;如果宽增加6厘米,体积就增加144立方厘米;如果高增加7厘米,体积增加210立方厘米。求原来长方体的表面积。
28.(6分)(2021·江苏·淮阴师范学院第一附属小学六年级期中)张大爷准备用铁皮做一个长方体烟囱,烟囱高8分米,底面是边长为2分米的正方形,做这个烟囱至少需要多少平方分米铁皮?
29.(6分)(2021·江苏省南京市南化第四小学六年级期中)一个无盖的长方体铁皮水槽,长8分米,宽4分米,高2.5分米。
(1)做这个水槽需要多少平方分米的铁皮?
(2)这个水槽装满水,水重多少千克?(1升水重1千克)
30.(6分)(2022·江苏泰州·六年级期末)光明小学准备修建一个长6米、宽3米、深50厘米的沙坑。
(1)如果要在沙坑的四周和底面抹上水泥,抹水泥的面积是多少平方米?
(2)如果要在沙坑里填满黄沙,准备黄沙19吨,够不够?(每立方米黄沙重2.4吨)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.B
【解析】
【分析】
正方体展开图有四种类型,即“一四一”,“二二二“、“三三”、“一三二”,据此解答。
【详解】
A.属于正方体展开图“二二二”类型;
B.不属于正方体展开图;
C.属于正方体展开图“一四一”类型;
D.属于正方体展开图“一三二”类型。
答案:B
【点评】
主要考查正方体展开图,熟练掌握正方体展开图的特征,也可以动手实践操作下。
2.C
【解析】
【分析】
根据正方体的体积=棱长×棱长×棱长,以及积的变化规律:因数乘几或除以几(0除外),积就乘几或除以几;据此解答。
【详解】
2×2×2
=4×2
=8
正方体的棱长扩大到原来的2倍,那么体积扩大到原来的8倍。
答案:C
【点评】
掌握正方体的体积计算公式以及积的变化规律是解题的关键。
3.B
【解析】
【分析】
根据生活经验,对体积单位和数据的大小认识,可知计量一个文具盒的体积用“立方厘米”做单位。
【详解】
由分析可知;一个文具盒的体积大约180立方厘米。
答案:B
【点评】
此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
4.B
【解析】
【分析】
首先根据长方体的体积公式:v=abh,把数据代入公式求出这个木桶的体积,由于木桶的木板有一定的厚度,所以它的容积要小于它的体积,据此解答。
【详解】
6×5×4=120(立方分米)
120立方分米=120升
木桶的容积<120升,100升最符合题意。
答案:B
【点评】
此题主要考查长方体的体积公式的灵活运用,关键是熟记公式。
5.B
【解析】
【分析】
将长方体切成两个,如果切面的长和宽是最大值,那么表面积增加的是最多的,由此可知,长10cm,宽8cm,增加的是2个面的面积,用10×8×2即可解答。
【详解】
10×8×2
=80×2
=160(平方厘米)
答案:B
【点评】
此题主要考查学生对长方体表面积的理解与认识。
6.B
【解析】
【分析】
由正方体的特征可知:正方体共有12条棱,且每条棱长都相等,棱长总和是48分米,则可以求出每条棱的长度,进而利用正方体的表面积公式就可以求出其表面积。
【详解】
棱长:48÷12=4(分米)
正方体的表面积:
4×4×6
=16×6,
=96(平方分米)
答案:B
【点评】
解答此题的主要依据是:正方体共有12条棱长,且每条棱长都相等以及正方体的表面积公式。
7.D
【解析】
【分析】
通过观察图形可知,一个长方体正好能切成3个棱长是4厘米的正方体,3个正方体的表面积之和比原来长方体增加了4个切面的面积,根据正方形的面积公式:S=a2,把数据代入公式解答。
【详解】
4×4×4
=16×4
=64(平方厘米)
答案:D
【点评】
此题考查的目的是理解掌握长方体、正方体表面积的意义,关键是明确:一个长方体正好能切成3个棱长是4厘米的正方体,3个正方体的表面积之和比原来长方体增加了4个切面的面积。
8.C
【解析】
【分析】
根据1立方米与1立方分米的进率是1000即可判断。
【详解】
因为1立方米=1000立方分米,
也就相当于1立方米里面有1000个1立方分米,
所以体积是1立方米的正方体木块,可以切割成1000个1立方分米的小正方体木块;
答案:C
【点评】
此题也可以利用画图操作,进行观察,根据1米=10分米,每个棱上可以割成10个,一共可割成:10×10×10=1000个,然后选出答案即可。
9.##0.75 ##0.012
【解析】
【分析】
低级单位化高级单位,除以单位之间的进率。1时=60分,1立方分米=1升=1000毫升。
【详解】
45÷60=,则45分=时;
12÷1000=,则12毫升=立方分米。
【点评】
考查单位的换算。要熟练掌握单位之间的进率和换算方法。
10.92 340 400
【解析】
【分析】
根据长方体的棱长总和=(长+宽+高)×4,代入数据,求出这个长方体的棱长总和;再根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,求出至少要用白纸的面积;再根据长方体体积公式:长×宽×高,代入数据,即可解答。
【详解】
棱长总和:
(10+8+5)×4
=(18+5)×4
=23×4
=92(厘米)
表面积:
(10×8+10×5+8×5)×2
=(80+50+40)×2
=(130+40)×2
=170×2
=340(平方厘米)
10×8×5
=80×5
=400(立方厘米)
【点评】
根据长方体的棱长总和公式、表面积公式、体积公式进行解答,关键是熟记公式。
11.4 8
【解析】
【分析】
根据长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,设出原来的长、宽、高,利用长方体的表面积公式表示出其表面积,再用现在的长、宽、高,得出现在的表面积,用现在的表面积除以原来的表面积,就是表面积扩大的倍数,同理得出体积扩大的倍数。
【详解】
令原来的长、宽、高分别为a、b、h,
则原来的表面积:(ab+ah+bh)×2
现在的表面积:(2a×2b+2a×2h+2b×2h)×2
=(4ab+4ah+4bh)×2
=(ab+ah+bh)×8
现在的表面积是原来的:[(ab+ah+bh)×8]÷[(ab+ah+bh)×2]=4
原来的体积:abh
现在的体积:2a×2b×2h=8abh
现在的体积是原来的:8abh÷abh=8
所以一个长方体的长、宽、高都扩大到原来的2倍,则表面积扩大到原来的4倍,体积扩大到原来的8倍。
【点评】
此题主要考查长方体的表面积公式、体积公式的灵活运用,以及因数与积的变化规律的应用。
12.150 125
【解析】
【分析】
由题意得正方体的棱长=总和÷12,再根据正方体的表面积=6a2计算出表面积,根据计算体积。
【详解】
60÷12=5(厘米)
6×5×5=150(平方厘米)
5×5×5=125(立方厘米)
【点评】
根据正方体的棱长=总和÷12求出正方体的棱长是解题的关键。
13.96 64 8
【解析】
【分析】
①根据正方体的表面积和体积公式即可求得其表面积和体积;
②抓住正方体分割前后的体积不变,即可得出小正方体的个数。
【详解】
4×4×6=96(平方厘米)
4×4×4=64(立方厘米)
2×2×2=8(立方厘米)
64÷8=8(个)
则棱长是4厘米的正方体的表面积是96平方厘米,体积是64立方厘米,可以截成棱长是2厘米的正方体8个。
【点评】
此题考查了正方体表面积和体积公式的灵活应用,以及正方体分割的方法。
14.7.2
【解析】
【分析】
根据题意可知,把长12米的长方体材料,平均锯成3段后,表面积比原来增加2.4平方米,表面积增加的是4个截面的面积,据此可以求出每个截面的面积,然后根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】
2.4÷4×12
=0.6×12
=7.2(立方米)
原来这根木料的体积是7.2立方米。
【点评】
此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是求出长方体的底面积。
15.7 6 42 27
【解析】
【分析】
根据长方体的特征,这个长方体的6个面都是长方形,相对的面的面积相等。由题意可知,这个长方体纸盒的最大面是底面,长是7分米,宽是6分米;最小面是左右面,长是6分米,宽是4.5分米;根据长方形的面积公式:S=ab,分别求出它们的面积。
【详解】
最大面的长是7分米,宽是6分米,面积是:7×6=42(平方分米);
最小面的长是6分米,宽是4.5分米,面积是:6×4.5=27(平方分米)。
【点评】
此题主要考查长方体表面积的计算,需要根据长方形的面积公式解答。
16.6
【解析】
【分析】
锯成3段后,表面积增加了4个横截面的面积,因为表面积是增加了24平方米,由此即可求出横截面的面积是24÷4=6平方米,据此解答即可。
【详解】
根据分析,这根木料的横截面是:
24÷4=6(平方米)
【点评】
抓住长方体的切割特点和增加的表面积求出长方体的横截面的面积是解决此题的关键。
17.×
【解析】
【分析】
容积是指物体所容纳物体的体积,两个体积一样大的盒子,盒皮的厚度不一样,所容纳物体的体积就不一样,盒皮厚的容纳的体积少些,盒皮薄的容纳的体积多些,如果厚度一样,容积就一样大,据此解答即可。
【详解】
两个体积一样大的盒子,它们的容积一定同样大的说法是错误的,应该是容积不一定同样大。
答案:×
【点评】
此题考查容积的意义,解决此题的关键是容积的定义,注重盒皮的厚度。
18.×
【解析】
【分析】
由“一个棱长为4厘米的正方体”可以求出正方体的1个面的面积,则切出的每个小长方体的表面积都等于原正方体的表面积的一半与一个正方体的面的面积之和,据此即可解答。
【详解】
4×4×6÷2+4×4
=48+16
=64(平方厘米)
答案:×
【点评】
此题考查的是长方体表面积和体积计算,解答此题的关键是明确每个小长方体的表面积都包括哪几个部分。
19.×
【解析】
【分析】
正方体的棱长=棱长总和÷12,据此求出正方体的棱长,正方体的体积=棱长×棱长×棱长,正方体的表面积=棱长×棱长×6,据此解答。
【详解】
36÷12=3(厘米)
体积:3×3×3=27(立方厘米),表面积:3×3×6=54(平方厘米)
体积和表面积不是同一种量,无法比较,原题说法错误。
答案:×
【点评】
物体的体积和表面积不是同一种量,无法进行比较。
20.×
【解析】
【分析】
物体的表面或封闭图形的大小,叫做它们的面积。体积是指物体所占空间的大小。表面积和体积意义不同,无法比较,据此分析。
【详解】
一个棱长为6cm的正方体,它的表面积和体积无法比较,所以原题说法错误。
答案:×
【点评】
正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长。
21.190平方厘米
【解析】
【分析】
观察图形可知,棱长5厘米的正方体的表面积,与长是5厘米,宽是2厘米的长方体的侧面积之和,四个面相等,根据正方体表面积公式:棱长×棱长×6,长方体侧面积公式:长×宽×4,代入数据,即可解答。
【详解】
5×5×6+5×2×4
=25×6+10×4
=150+40
=190(平方厘米)
22.见详解
【解析】
【分析】
根据图可知,这个完全涂上黑色的小正方形的四周有4个小正方形被涂上一半,根据正方体展开图的特征,即可知道图2黑色区域的小正方形,它的左边和右边的小正方形各涂了一半阴影,即竖直涂上一半的阴影,这两部分阴影和2黑色区域阴影部分挨着;它下面涂色部分是横着的阴影,也和它挨着;第4个小正方形是展开图的最右上角的小正方形,它的涂色区域是水平的一半,再上面。
【详解】
由分析可知:
【点评】
主要考查正方体展开图,可以动手实际操作一下。
23.2.2平方米;150升
【解析】
【分析】
由于鱼缸是无盖的,根据长方体5个面的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解,再根据1平方米=100平方分米,转换单位即可;由于注入2.5分米深的水,则此时水形成的形状是一个长10分米,宽6分米,高2.5分米的长方体,根据长方体的体积公式:长×宽×高,把数代入公式即可求解,再根据1升=1立方分米,由此转换单位。
【详解】
10×6+(10×5+6×5)×2
=60+(50+30)×2
=60+80×2
=60+160
=220(平方分米)
220平方分米=2.2平方米。
10×6×2.5
=60×2.5
=150(立方分米)
150立方分米=150升
答:做这样一个鱼缸需要玻璃2.2平方米;这时鱼缸中有水150升。
【点评】
主要考查长方体的表面积和体积公式,熟练掌握它们的公式并灵活运用,要注意转换单位。
24.0.9平方米,81千克
【解析】
【分析】
铁皮的面积=(长×高+宽×高)×2+长×宽,代入数据计算即可;水的体积=长×宽×高,再乘每升水的质量即可。
【详解】
(6×3+4.5×3)×2+6×4.5
=(18+13.5)×2+27
=63+27
=90(平方分米)
=0.9(平方米);
6×4.5×3
=27×3
=81(立方分米)
=81(升)
81×1=81(千克)
答:做这个水箱至少需要铁皮0.9平方米,这个水箱最多能装水81千克。
【点评】
此题考查了长方体表面积和体积的综合应用,需牢记公式认真计算,注意单位换算。
25.见详解
【解析】
【分析】
长方体的体积=长×宽×高,又长×宽是长方体的底面积,由此推知长方体的体积=底面积×高,进而推测出上、下底面都是等腰梯形的物体体积公式;据此解答。
【详解】
猜测∶V=Sh
理由∶先求出梯形的面积S=(上底+下底)×高÷2,四棱柱的体积V则为梯形的面积S×棱柱的高h。
【点评】
通过对长方体体积公式的理解,合理推测即可。
26.81平方分米
【解析】
【分析】
先根据1立方分米=1升换算出油的体积是多少立方分米,然后用油的体积除以长方体油箱的底面积,即可得到油的深度,再根据长方体表面积计算公式求出油与油箱内壁的接触面积。
【详解】
54升=54立方分米
油的深度:
54÷(3×3)
=54÷9
=6(分米)
油与油箱内壁的接触面积:
3×6×4+3×3
=72+9
=81(平方分米)
答:油与油箱内壁的接触面积是81平方分米。
【点评】
此题主要考查长方体的体积的计算方法的灵活应用.注意体积单位和容积单位的换算。
27.148平方厘米
【解析】
【分析】
当长增加5厘米,则宽和高不变,此时增加部分的体积:5×宽×高=100,由此即可求出宽×高=20平方厘米;宽增加6厘米,则长和高不变,增加部分的体积:长×高×6=144,则长×高=24平方厘米;高增加7厘米,则长和宽不变,增加部分的体积:长×宽×7=210,则长×宽=30平方厘米,之后根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,把数代入公式即可求解。
【详解】
宽×高:100÷5=20(平方厘米)
长×高:144÷6=24(平方厘米)
长×宽:210÷7=30(平方厘米)
表面积:(20+24+30)×2
=74×2
=148(平方厘米)
答:原来长方体的表面积是148平方厘米。
【点评】
此题关键是理解长增加宽和高不变,宽增加长和高不变,高增加长和宽不变。根据长方体的表面积公式解答即可。
28.64平方分米
【解析】
【分析】
由于长方体烟囱有4个面,没有上下两个面,即根据长方体的表面积公式:(长×高+宽×高)×2,把数代入公式即可。
【详解】
(8×2+8×2)×2
=(16+16)×2
=32×2
=64(平方分米)
答:做这个烟囱至少需要64平方分米铁皮。
【点评】
主要考查长方体的表面积公式,要注意联系生活实际看这个长方体有几个面。
29.(1)92平方分米;
(2)80千克
【解析】
【分析】
(1)由题意可知,做这个水槽需要前后、左右和下共5个面,则需要“长×高×2+宽×高×2+长×宽”平方分米的铁皮;
(2)根据 “长方体的容积=长×宽×高”求出水槽中水的体积,再乘1升水的质量即可。
【详解】
(1)8×4+8×2.5×2+4×2.5×2
=32+40+20
=92(平方分米)
答:做这个水槽需要92平方分米的铁皮。
(2)8×4×2.5×1
=32×2.5
=80(千克)
答:水重80千克。
【点评】
熟练掌握长方体表面积和体积的计算方法是解答的关键。
30.(1)27平方米;(2)不够
【解析】
【分析】
(1)根据题意,求出这个沙坑的底面积加上四个侧面积,根据长方体的表面积公式:长×宽+(长×高+宽×高)×2,代入数据,即可解答;
(2)根据长方体的体积公式:长×宽×高,用体积×2.4,再和19吨比较,大于19吨,就不够,小于19吨,就够。
【详解】
(1)50厘米=0.5米
6×3+(6×0.5+3×0.5)×2
=18+(3+1.5)×2
=18+4.5×2
=18+9
=27(平方米)
答:抹水泥的面积是27平方米。
(2)6×3×0.5×2.4
=18×0.5×2.4
=9×2.4
=21.6(吨)
21.6>19
准备19吨黄沙不够。
答:不够。
【点评】
考查长方体表面积公式、体积公式的应用,注意单位名数的统一。
答案第1页,共2页
答案第1页,共2页
