八年级数学上册试题 1.2一定是直角三角形吗同步练习-北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 1.2一定是直角三角形吗同步练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 828.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 14:24:05 | ||
图片预览



文档简介
1.2一定是直角三角形吗
第一课时
一、单选题
1.五根小木棒,其长度分别为,,,,,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
2.下列各组数中,不能作直角三角形三边长的是( ).
A.3、4、5 B.5、12 、13 C.7、24、25 D.7、9、13
3.下列各组数据不是勾股数的是( )
A.2,3,4 B.3,4,5 C.5,12,13 D.6,8,10
4.如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
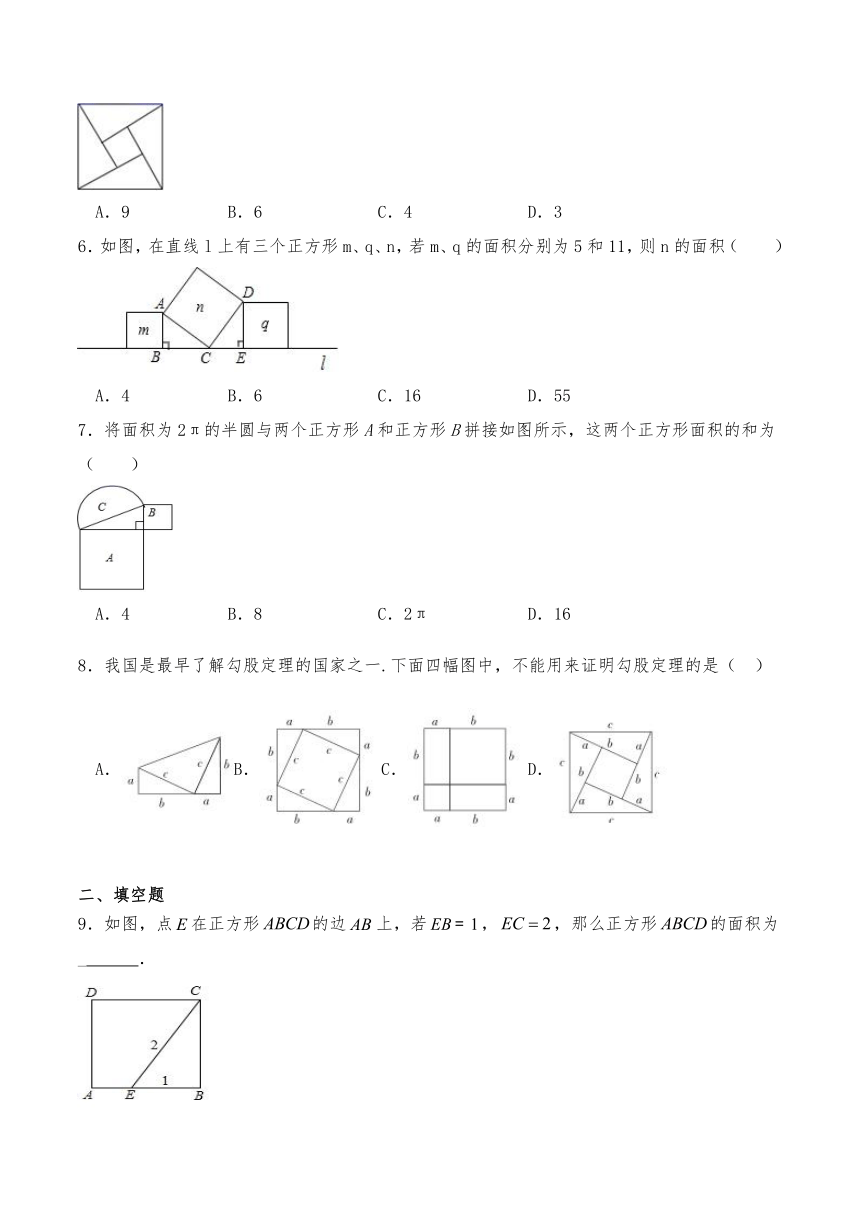
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为
A.9 B.6 C.4 D.3
6.如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( )
A.4 B.6 C.16 D.55
7.将面积为2π的半圆与两个正方形A和正方形B拼接如图所示,这两个正方形面积的和为( )
A.4 B.8 C.2π D.16
8.我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )
A.B.C. D.
二、填空题
9.如图,点在正方形的边上,若,,那么正方形的面积为_ .
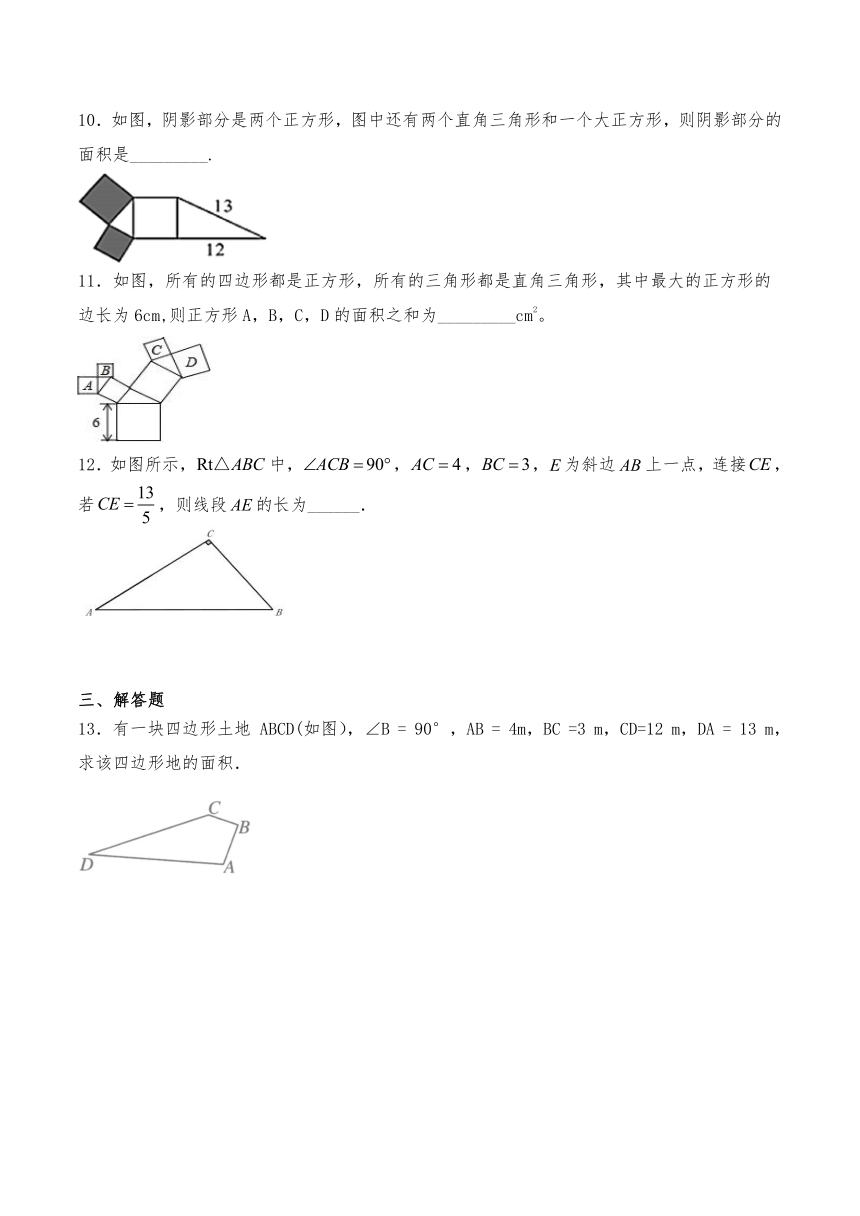
10.如图,阴影部分是两个正方形,图中还有两个直角三角形和一个大正方形,则阴影部分的面积是_________.
11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为6cm,则正方形A,B,C,D的面积之和为_________cm2。
12.如图所示,中,,,,为斜边上一点,连接,若,则线段的长为______.
三、解答题
13.有一块四边形土地 ABCD(如图),∠B = 90°,AB = 4m,BC =3 m,CD=12 m,DA = 13 m,求该四边形地的面积.
14.某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
15.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.
将两个全等的直角三角形按如图所示摆放,其中∠DAB = 90°,求证:a2+b2=c2.
第二课时
一、单选题
1.下列各组数据,是勾股数的是( )
A.,, B.32,42,52
C.0.5,1.2,1.3 D.12,16,20
2.满足下列条件的,不是直角三角形的是( )
A. B.
C. D.
3.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件不能判断△ABC是直角三角形的是( )
A.∠B=∠C+∠A B.a2=(b+c)(b﹣c)
C.∠A:∠B:∠C=3:4:5 D.a:b:c=3:4:5
4.已知,,是三角形的三边长,且,那么此三角形是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.等腰直角三角形 D.锐角三角形
5.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是( )
A. B. C. D.
6.下列说法中正确的是( )
A.在中,.
B.在中,.
C.在中,,.
D.、、是的三边,若,则是直角三角形.
7.下列命题①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a,b,c,(a>b=c),那么a2:b2:c2=2:1:1.其中正确的是( )
A.①② B.①③ C.①④ D.②④
8.如图,两个全等的直角三角形和一个等腰直角三角形恰好构成一个梯形.甲说:梯形的面积可以表示为,乙说:梯形的面积可以表示为,则有( )
A. B.
C. D.
9.给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若,,是勾股数,且最大,则一定有;
④若三个整数,,是直角三角形的三边长,则,,一定是勾股数.
其中正确的是 ( )
A.①② B.②③ C.③④ D.①④
10.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是64,小正方形的面积为4,直角三角形的两直角边长分别为a,b,且a> b . 那么下列结论:(1)a2+b2=64,(2)a-b=2,(3)ab=30,(4)a+b=2.正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
11.意大利著名画家达·芬奇用下图所示的方法证明了勾股定理.若设左图中空白部分的面积为,右图中空白部分的面积为,则下列表示的等式成立的是( )
A. B. C. D.
12.如图,四个全等的直角三角形围成一个正方形ABCD和正方形EFGH,即赵爽弦图,连接AC,FN交EF,GH分别于点M,N已知AH=3DH,且S正方形ABCD,则图中阴影部分的面积之和为( )
A. B. C. D.
二、填空题
13.若三角形的三边长是6,8,,当的值为________时,该三角形是直角三角形.
14.一个三角形的三边长分别是,,,则此三角形是________.
15.如图,正方形网格中的△ABC,若小方格边长都为1,则△ABC是_____ 三角形.
16.如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=___s时,△PBQ为直角三角形.
17.如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.
(1)线段AB的长为__,BC的长为__,CD的长为__,AD的长为__;
(2)连接AC,通过计算△ACD的形状是__;△ABC的形状是__.
18.如图,OA=OB,OC=3,BC=1,数轴上点A表示的数是_____.
19.如图,中,,,直线、、分别通过、、三点,且.若与的距离为3,与的距离为5,则的面积为___________.
20.如图,在中,,,,点是边的中点,点是射线上的一个动点,交的延长线于点,交边于点.当时,的长为______.
21.曾任美国总统的加菲尔德曾经给出了一种勾股定理的证明方法.如图,该图形整体上拼成了一个直角梯形,所以它的面积有两种表示方法,既可以表示为_______,又可以表示为_______.对比两种表示方法可得________,化简,可得.
22.如图在中,,,,为等边三角形,点为围成的区域(包括各边)内的一点,过点作,交直线于点,作,交直线于点,则平行线与间距离的最大值为_________.
三、解答题
23.如图所示的一块地,AD=9 m,CD=12 m,∠ADC=90°,AB=39 m,BC=36 m,求这块地的面积.
24.如图所示,在平面直角坐标系中,点A、B的坐标分别为A(3,1),B(2,4),△OAB是直角三角形吗?借助于网格,证明你的结论.
25.在解答“判断由长为,2,的三条线段组成的三角形是不是直角三角形”一题中,小明是这样做的,你认为小明的解答正确吗?请说明理由.
解:设a=,b=2,c=.
∵a2+b2=()2+22=,c2=()2=,
∴a2+b2≠c2,
∴这三条线段组成的三角形不是直角三角形.
26.观察下列各组勾股数的组成特点,你能求出第7组勾股数a,b,c各是多少吗?第n组呢?
第 1 组:3=2×1+1,4=2×1×(1+1),5=2×1×(1 + 1)+1;
第 2 组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1) + 1;
第 3 组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1) + 1;
第 4 组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1) + 1;
…;
第 7 组:a,b,c.
27.如图,在△ABC中,AB=AC=4,P为BC边上任意一点.
(1)求证:AP2+PB·PC=16.
(2)若BC边上有100个不同的点(不与点B,C重合)P1,P2,…,P100,设mi=APi2+PiB·PiC(i=1,2,…,100).求m1+m2+…+m100的值.
28.勾股定理是人类最伟大的十个科学发现之一,在《周髀算经》中就有“若勾三,股四,则弦五”的记载,汉代数学家赵爽为证明勾股定理创制的“赵爽弦图”也流传至今.迄今为止己有多种证明勾股定理的方法.下面是数学课上创新小组验证过程的一部分.请认真阅读并根据他们的思路将后续的过程补充完整:将两张全等的直角三角形纸片按图所示摆放,其中,点 在线段上,点在边两侧,试证明: .
29.如图,在和中,,,.
(1)若,,,求的大小;
(2)猜想线段与的关系,并证明你的猜想.
30.勾股定理现约有500种证明方法,是用代数思想解决几何问题的最重要的工具之一.中国古代最早对勾股定理进行证明的是三国时期吴国的数学家赵爽,赵爽创制了如图1所示的“勾股圆方图”,在该图中,以弦为边长所得到的正方形是由4个全等的直角三角形再加上中间的小正方形组成的,其中,.
(1)请利用面积相等证明勾股定理;
(2)在图1中,若大正方形的面积是13,,求小正方形的面积;
(3)图2是由“勾股圆方图”变化得到的,正方形由八个全等的直角三角形和正方形拼接而成,记图中正方形,正方形,正方形的面积分别为,,.若,求边的长度.
31.阅读理解:
(问题情境)
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
(探索新知)
从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积+4个直角三角形的面积.
从而得数学等式:(a+b)2=c2+4×ab,化简证得勾股定理:a2+b2=c2.
(初步运用)
(1)如图1,若b=2a,则小正方形面积:大正方形面积= ;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a=4,b=6,此时空白部分的面积为 ;
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC=3,求该风车状图案的面积.
(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
(迁移运用)
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?
带着这个疑问,小丽拼出图5的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
第一课时答案
一、单选题
C.D.A.D.D.C.D.C.
二、填空题
9..
10.25.
11.36.
12.或.
三、解答题
13.连接AC.
∵∠B=90°,
∴AC=(m),
∵52+122=132,
∴△ADC是直角三角形,且∠ACD=90,
∴S四边形ABCD()
14.解:过点A作AD⊥BC于点D,
设BD=x,则CD=14﹣x,在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2 , AD2=AC2﹣CD2 ,
∴AB2﹣BD2=AC2﹣CD2 ,即132﹣x2=152﹣(14﹣x)2 ,
解得x=5,
∴AD2=AB2﹣BD2=132﹣52=144,
∴AD=12(米),
花园的面积=×14×12=84 (m2 )
∴学校修建这个花园的费用=25×84=2100(元).
答:学校修建这个花园需要投资2100元.
15.如图,过点D作,交BC延长线于点F,连接BD,则,
由全等三角形的性质得:,
,
,
,
即,
整理得:.
第二课时答案
一、单选题
D.C.C.B.D.D.C.B.C.D.A.B.
二、填空题
13.100或28
14.直角三角形.
15.直角.
16.或.
17.(1),5,2,2;(2)等腰三角形,直角三角形
18..
19.17.
20.2.5或1.
21.; ; .
22..
三、解答题
23.解: 连接AC,则在Rt△ADC中,
AC2=CD2+AD2=122+92=225,
∴AC=15,
在△ABC中,AB2=1521,
AC2+BC2=152+362=1521,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴S△ABC-S△ACD=AC·BC-AD·CD=×15×36-×12×9=270-54=216.
答:这块地的面积是216平方米.
24.解:∵ OA2=OA12+A1A2=32+12=10,
OB2=OB12+B1B2=22+42=20,
AB2=AC2+BC2=12+32=10,
∴OA2+AB2=OB2.
∴△OAB是以OB为斜边的等腰直角三角形.
25.小明的做法不正确,
理由是:∵()2+()2=22,
∴这三条线段组成的三角形是直角三角形
26.∵第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,
第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,
第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,
第四组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,
∴第七组勾股数是a=2×7+1=15,b=2×7×(7+1)=112,c=2×7×(7+1)+1=113,即15,112,113;
第n组勾股数是2n+1,2n(n+1),2n(n+1)+1.
27.(1)过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=CD,∠ADB=∠ADC=90°,
∴AP2+PB·PC=AP2+(PD+BD)(CD-PD)=AP2+CD2-PD2.
∵AP2-PD2=AD2,
∴AP2+PB·PC=AD2+CD2=AC2=16.
(2)由(1)知mi=APi2+PiB·PiC=16,
∴m1=m2=…=m100=16,
∴m1+m2+…+m100=16×100=1600.
28.证明:连结,作延长线于,则
∴AB=AD=C
∠ADE=∠DAE=900
∴∠BAC=∠DAE=900
即,
∴
∴
即有:
∴
29.解:(1)∵,,,∴,
∵,∴,
∴.
(2)猜想:,,
∵,
∴,
∵, ,
∴≌,
∴,
如图,延长交于点,
∵≌,∴,
∴
∴,
∴.
30.解:(1)∵
∴,
∴小正方形的边长=
又大正方形的边长为
∴正方形的面积为,4个全等直角三角形的面积和为,正方形的面积为,
由“大正方形的面积=4个全等直角三角形的面积+小正方形的面积”得;
∴
经过整理可得
(2)∵大正方形的面积是13,
∴
∵,且
∴
∴(负值舍去)
∴
∴小正方形的面积为1;
(3)∵正方形由八个全等的直角三角形和正方形拼接而成,
∴,,
∴正方形的边长为,
∴正方形的面积为.
而正方形的边长为,正方形的边长为,
∴正方形的面积为,正方形的面积为,
∴,
整理得,,
∴(负值舍去)
31.解:【初步运用】(1)由题意:b=2a,c=,
∴小正方形面积:大正方形面积=5a2:9a2=5:9,
故答案为:5:9;
(2)空白部分的面积为=52﹣2××4×6=28,
故答案为:28;
(3)24÷4=6,
设AC=x,依题意有:(x+3)2+32=(6﹣x)2,
解得x=1,
∴面积为:×(3+1)×3×4
=×4×3×4
=24,
故该飞镖状图案的面积是24;
(4)将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=40,
∴S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=40,
∴x+4y=,
∴S2=x+4y=,
故答案为:;
[迁移运用]结论:a2+b2﹣ab=c2.
理由:由题意:大正三角形面积=三个全等三角形面积+小正三角形面积,
可得:(a+b)×k(a+b)=3××b×ka+×c×ck,
∴(a+b)2=3ab+c2,
∴a2+b2﹣ab=c2.
第一课时
一、单选题
1.五根小木棒,其长度分别为,,,,,现将它们摆成两个直角三角形,如图,其中正确的是( )
A. B.
C. D.
2.下列各组数中,不能作直角三角形三边长的是( ).
A.3、4、5 B.5、12 、13 C.7、24、25 D.7、9、13
3.下列各组数据不是勾股数的是( )
A.2,3,4 B.3,4,5 C.5,12,13 D.6,8,10
4.如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为
A.9 B.6 C.4 D.3
6.如图,在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( )
A.4 B.6 C.16 D.55
7.将面积为2π的半圆与两个正方形A和正方形B拼接如图所示,这两个正方形面积的和为( )
A.4 B.8 C.2π D.16
8.我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )
A.B.C. D.
二、填空题
9.如图,点在正方形的边上,若,,那么正方形的面积为_ .
10.如图,阴影部分是两个正方形,图中还有两个直角三角形和一个大正方形,则阴影部分的面积是_________.
11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为6cm,则正方形A,B,C,D的面积之和为_________cm2。
12.如图所示,中,,,,为斜边上一点,连接,若,则线段的长为______.
三、解答题
13.有一块四边形土地 ABCD(如图),∠B = 90°,AB = 4m,BC =3 m,CD=12 m,DA = 13 m,求该四边形地的面积.
14.某小区内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化小区环境,预计花园每平方米造价为25元,小区修建这个花园需要投资多少元?
15.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.
将两个全等的直角三角形按如图所示摆放,其中∠DAB = 90°,求证:a2+b2=c2.
第二课时
一、单选题
1.下列各组数据,是勾股数的是( )
A.,, B.32,42,52
C.0.5,1.2,1.3 D.12,16,20
2.满足下列条件的,不是直角三角形的是( )
A. B.
C. D.
3.在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,下列条件不能判断△ABC是直角三角形的是( )
A.∠B=∠C+∠A B.a2=(b+c)(b﹣c)
C.∠A:∠B:∠C=3:4:5 D.a:b:c=3:4:5
4.已知,,是三角形的三边长,且,那么此三角形是( )
A.以为斜边的直角三角形 B.以为斜边的直角三角形
C.等腰直角三角形 D.锐角三角形
5.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是( )
A. B. C. D.
6.下列说法中正确的是( )
A.在中,.
B.在中,.
C.在中,,.
D.、、是的三边,若,则是直角三角形.
7.下列命题①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果三角形的三个内角的度数比是3:4:5,那么这个三角形是直角三角形;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a,b,c,(a>b=c),那么a2:b2:c2=2:1:1.其中正确的是( )
A.①② B.①③ C.①④ D.②④
8.如图,两个全等的直角三角形和一个等腰直角三角形恰好构成一个梯形.甲说:梯形的面积可以表示为,乙说:梯形的面积可以表示为,则有( )
A. B.
C. D.
9.给出下列四个说法:
①由于0.3,0.4,0.5不是勾股数,所以以0.3,0.4,0.5为边长的三角形不是直角三角形;
②由于以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数;
③若,,是勾股数,且最大,则一定有;
④若三个整数,,是直角三角形的三边长,则,,一定是勾股数.
其中正确的是 ( )
A.①② B.②③ C.③④ D.①④
10.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是64,小正方形的面积为4,直角三角形的两直角边长分别为a,b,且a> b . 那么下列结论:(1)a2+b2=64,(2)a-b=2,(3)ab=30,(4)a+b=2.正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
11.意大利著名画家达·芬奇用下图所示的方法证明了勾股定理.若设左图中空白部分的面积为,右图中空白部分的面积为,则下列表示的等式成立的是( )
A. B. C. D.
12.如图,四个全等的直角三角形围成一个正方形ABCD和正方形EFGH,即赵爽弦图,连接AC,FN交EF,GH分别于点M,N已知AH=3DH,且S正方形ABCD,则图中阴影部分的面积之和为( )
A. B. C. D.
二、填空题
13.若三角形的三边长是6,8,,当的值为________时,该三角形是直角三角形.
14.一个三角形的三边长分别是,,,则此三角形是________.
15.如图,正方形网格中的△ABC,若小方格边长都为1,则△ABC是_____ 三角形.
16.如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=___s时,△PBQ为直角三角形.
17.如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.
(1)线段AB的长为__,BC的长为__,CD的长为__,AD的长为__;
(2)连接AC,通过计算△ACD的形状是__;△ABC的形状是__.
18.如图,OA=OB,OC=3,BC=1,数轴上点A表示的数是_____.
19.如图,中,,,直线、、分别通过、、三点,且.若与的距离为3,与的距离为5,则的面积为___________.
20.如图,在中,,,,点是边的中点,点是射线上的一个动点,交的延长线于点,交边于点.当时,的长为______.
21.曾任美国总统的加菲尔德曾经给出了一种勾股定理的证明方法.如图,该图形整体上拼成了一个直角梯形,所以它的面积有两种表示方法,既可以表示为_______,又可以表示为_______.对比两种表示方法可得________,化简,可得.
22.如图在中,,,,为等边三角形,点为围成的区域(包括各边)内的一点,过点作,交直线于点,作,交直线于点,则平行线与间距离的最大值为_________.
三、解答题
23.如图所示的一块地,AD=9 m,CD=12 m,∠ADC=90°,AB=39 m,BC=36 m,求这块地的面积.
24.如图所示,在平面直角坐标系中,点A、B的坐标分别为A(3,1),B(2,4),△OAB是直角三角形吗?借助于网格,证明你的结论.
25.在解答“判断由长为,2,的三条线段组成的三角形是不是直角三角形”一题中,小明是这样做的,你认为小明的解答正确吗?请说明理由.
解:设a=,b=2,c=.
∵a2+b2=()2+22=,c2=()2=,
∴a2+b2≠c2,
∴这三条线段组成的三角形不是直角三角形.
26.观察下列各组勾股数的组成特点,你能求出第7组勾股数a,b,c各是多少吗?第n组呢?
第 1 组:3=2×1+1,4=2×1×(1+1),5=2×1×(1 + 1)+1;
第 2 组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1) + 1;
第 3 组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1) + 1;
第 4 组:9=2×4+1,40=2×4×(4+1),41=2×4×(4+1) + 1;
…;
第 7 组:a,b,c.
27.如图,在△ABC中,AB=AC=4,P为BC边上任意一点.
(1)求证:AP2+PB·PC=16.
(2)若BC边上有100个不同的点(不与点B,C重合)P1,P2,…,P100,设mi=APi2+PiB·PiC(i=1,2,…,100).求m1+m2+…+m100的值.
28.勾股定理是人类最伟大的十个科学发现之一,在《周髀算经》中就有“若勾三,股四,则弦五”的记载,汉代数学家赵爽为证明勾股定理创制的“赵爽弦图”也流传至今.迄今为止己有多种证明勾股定理的方法.下面是数学课上创新小组验证过程的一部分.请认真阅读并根据他们的思路将后续的过程补充完整:将两张全等的直角三角形纸片按图所示摆放,其中,点 在线段上,点在边两侧,试证明: .
29.如图,在和中,,,.
(1)若,,,求的大小;
(2)猜想线段与的关系,并证明你的猜想.
30.勾股定理现约有500种证明方法,是用代数思想解决几何问题的最重要的工具之一.中国古代最早对勾股定理进行证明的是三国时期吴国的数学家赵爽,赵爽创制了如图1所示的“勾股圆方图”,在该图中,以弦为边长所得到的正方形是由4个全等的直角三角形再加上中间的小正方形组成的,其中,.
(1)请利用面积相等证明勾股定理;
(2)在图1中,若大正方形的面积是13,,求小正方形的面积;
(3)图2是由“勾股圆方图”变化得到的,正方形由八个全等的直角三角形和正方形拼接而成,记图中正方形,正方形,正方形的面积分别为,,.若,求边的长度.
31.阅读理解:
(问题情境)
教材中小明用4张全等的直角三角形纸片拼成图1,利用此图,可以验证勾股定理吗?
(探索新知)
从面积的角度思考,不难发现:
大正方形的面积=小正方形的面积+4个直角三角形的面积.
从而得数学等式:(a+b)2=c2+4×ab,化简证得勾股定理:a2+b2=c2.
(初步运用)
(1)如图1,若b=2a,则小正方形面积:大正方形面积= ;
(2)现将图1中上方的两直角三角形向内折叠,如图2,若a=4,b=6,此时空白部分的面积为 ;
(3)如图3,将这四个直角三角形紧密地拼接,形成风车状,已知外围轮廓(实线)的周长为24,OC=3,求该风车状图案的面积.
(4)如图4,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,则S2= .
(迁移运用)
如果用三张含60°的全等三角形纸片,能否拼成一个特殊图形呢?
带着这个疑问,小丽拼出图5的等边三角形,你能否仿照勾股定理的验证,发现含60°的三角形三边a、b、c之间的关系,写出此等量关系式及其推导过程.
第一课时答案
一、单选题
C.D.A.D.D.C.D.C.
二、填空题
9..
10.25.
11.36.
12.或.
三、解答题
13.连接AC.
∵∠B=90°,
∴AC=(m),
∵52+122=132,
∴△ADC是直角三角形,且∠ACD=90,
∴S四边形ABCD()
14.解:过点A作AD⊥BC于点D,
设BD=x,则CD=14﹣x,在Rt△ABD与Rt△ACD中,
∵AD2=AB2﹣BD2 , AD2=AC2﹣CD2 ,
∴AB2﹣BD2=AC2﹣CD2 ,即132﹣x2=152﹣(14﹣x)2 ,
解得x=5,
∴AD2=AB2﹣BD2=132﹣52=144,
∴AD=12(米),
花园的面积=×14×12=84 (m2 )
∴学校修建这个花园的费用=25×84=2100(元).
答:学校修建这个花园需要投资2100元.
15.如图,过点D作,交BC延长线于点F,连接BD,则,
由全等三角形的性质得:,
,
,
,
即,
整理得:.
第二课时答案
一、单选题
D.C.C.B.D.D.C.B.C.D.A.B.
二、填空题
13.100或28
14.直角三角形.
15.直角.
16.或.
17.(1),5,2,2;(2)等腰三角形,直角三角形
18..
19.17.
20.2.5或1.
21.; ; .
22..
三、解答题
23.解: 连接AC,则在Rt△ADC中,
AC2=CD2+AD2=122+92=225,
∴AC=15,
在△ABC中,AB2=1521,
AC2+BC2=152+362=1521,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴S△ABC-S△ACD=AC·BC-AD·CD=×15×36-×12×9=270-54=216.
答:这块地的面积是216平方米.
24.解:∵ OA2=OA12+A1A2=32+12=10,
OB2=OB12+B1B2=22+42=20,
AB2=AC2+BC2=12+32=10,
∴OA2+AB2=OB2.
∴△OAB是以OB为斜边的等腰直角三角形.
25.小明的做法不正确,
理由是:∵()2+()2=22,
∴这三条线段组成的三角形是直角三角形
26.∵第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,
第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,
第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,
第四组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,
∴第七组勾股数是a=2×7+1=15,b=2×7×(7+1)=112,c=2×7×(7+1)+1=113,即15,112,113;
第n组勾股数是2n+1,2n(n+1),2n(n+1)+1.
27.(1)过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=CD,∠ADB=∠ADC=90°,
∴AP2+PB·PC=AP2+(PD+BD)(CD-PD)=AP2+CD2-PD2.
∵AP2-PD2=AD2,
∴AP2+PB·PC=AD2+CD2=AC2=16.
(2)由(1)知mi=APi2+PiB·PiC=16,
∴m1=m2=…=m100=16,
∴m1+m2+…+m100=16×100=1600.
28.证明:连结,作延长线于,则
∴AB=AD=C
∠ADE=∠DAE=900
∴∠BAC=∠DAE=900
即,
∴
∴
即有:
∴
29.解:(1)∵,,,∴,
∵,∴,
∴.
(2)猜想:,,
∵,
∴,
∵, ,
∴≌,
∴,
如图,延长交于点,
∵≌,∴,
∴
∴,
∴.
30.解:(1)∵
∴,
∴小正方形的边长=
又大正方形的边长为
∴正方形的面积为,4个全等直角三角形的面积和为,正方形的面积为,
由“大正方形的面积=4个全等直角三角形的面积+小正方形的面积”得;
∴
经过整理可得
(2)∵大正方形的面积是13,
∴
∵,且
∴
∴(负值舍去)
∴
∴小正方形的面积为1;
(3)∵正方形由八个全等的直角三角形和正方形拼接而成,
∴,,
∴正方形的边长为,
∴正方形的面积为.
而正方形的边长为,正方形的边长为,
∴正方形的面积为,正方形的面积为,
∴,
整理得,,
∴(负值舍去)
31.解:【初步运用】(1)由题意:b=2a,c=,
∴小正方形面积:大正方形面积=5a2:9a2=5:9,
故答案为:5:9;
(2)空白部分的面积为=52﹣2××4×6=28,
故答案为:28;
(3)24÷4=6,
设AC=x,依题意有:(x+3)2+32=(6﹣x)2,
解得x=1,
∴面积为:×(3+1)×3×4
=×4×3×4
=24,
故该飞镖状图案的面积是24;
(4)将四边形MTKN的面积设为x,将其余八个全等的三角形面积一个设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,S1+S2+S3=40,
∴S1=8y+x,S2=4y+x,S3=x,
∴S1+S2+S3=3x+12y=40,
∴x+4y=,
∴S2=x+4y=,
故答案为:;
[迁移运用]结论:a2+b2﹣ab=c2.
理由:由题意:大正三角形面积=三个全等三角形面积+小正三角形面积,
可得:(a+b)×k(a+b)=3××b×ka+×c×ck,
∴(a+b)2=3ab+c2,
∴a2+b2﹣ab=c2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
