北师大版数学九年级上册4.3 相似多边形同步练习(含答案)
文档属性
| 名称 | 北师大版数学九年级上册4.3 相似多边形同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 00:00:00 | ||
图片预览


文档简介
4.3 相似多边形
一、单选题
1.下列选项中的两个图形一定相似的是. ( )
A.两个等腰三角形 B.两个矩形 C.两个菱形 D.两个正五边形.
2.下列选项中,不是依据三角形全等知识解决问题的是( )
A.同一时刻,同一地点两栋等高建筑物影子一样长
B.工人师傅用角尺平分任意角
C.利用尺规作图,作一个角等于已知角
D.用放大镜观察蚂蚁的触角
3.在如图所示的图形中,形状相同的是( )
A.图①与图② B.图②与图③ C.图②与图④ D.图①与图④
4.用同一张底片洗出两张照片,一张为2寸,另一张为6寸,则这两张照片上的图像的大小比例为( )
A. B. C. D.不能确定
5.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为( )
A. B. C. D.
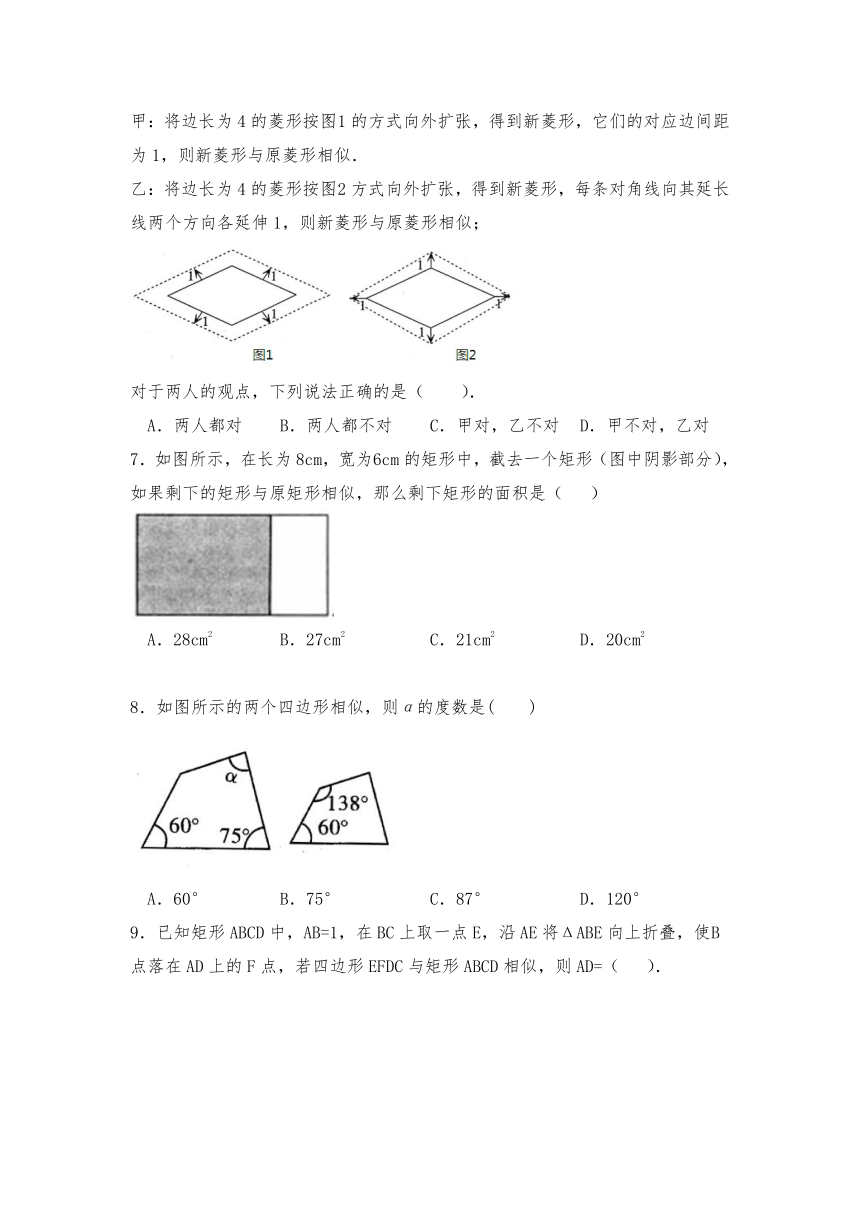
6.在研究相似问题时,甲、乙两同学的观点如下:
甲:将边长为4的菱形按图1的方式向外扩张,得到新菱形,它们的对应边间距为1,则新菱形与原菱形相似.
乙:将边长为4的菱形按图2方式向外扩张,得到新菱形,每条对角线向其延长线两个方向各延伸1,则新菱形与原菱形相似;
对于两人的观点,下列说法正确的是( ).
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
7.如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
8.如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
9.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将ΔABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).
A. B. C. D.2
10.如果两个相似多边形的面积比为9∶4,那么这两个相似多边形的相似比为( )
A.9∶4 B.2∶3 C.3∶2 D.81∶16
二、填空题
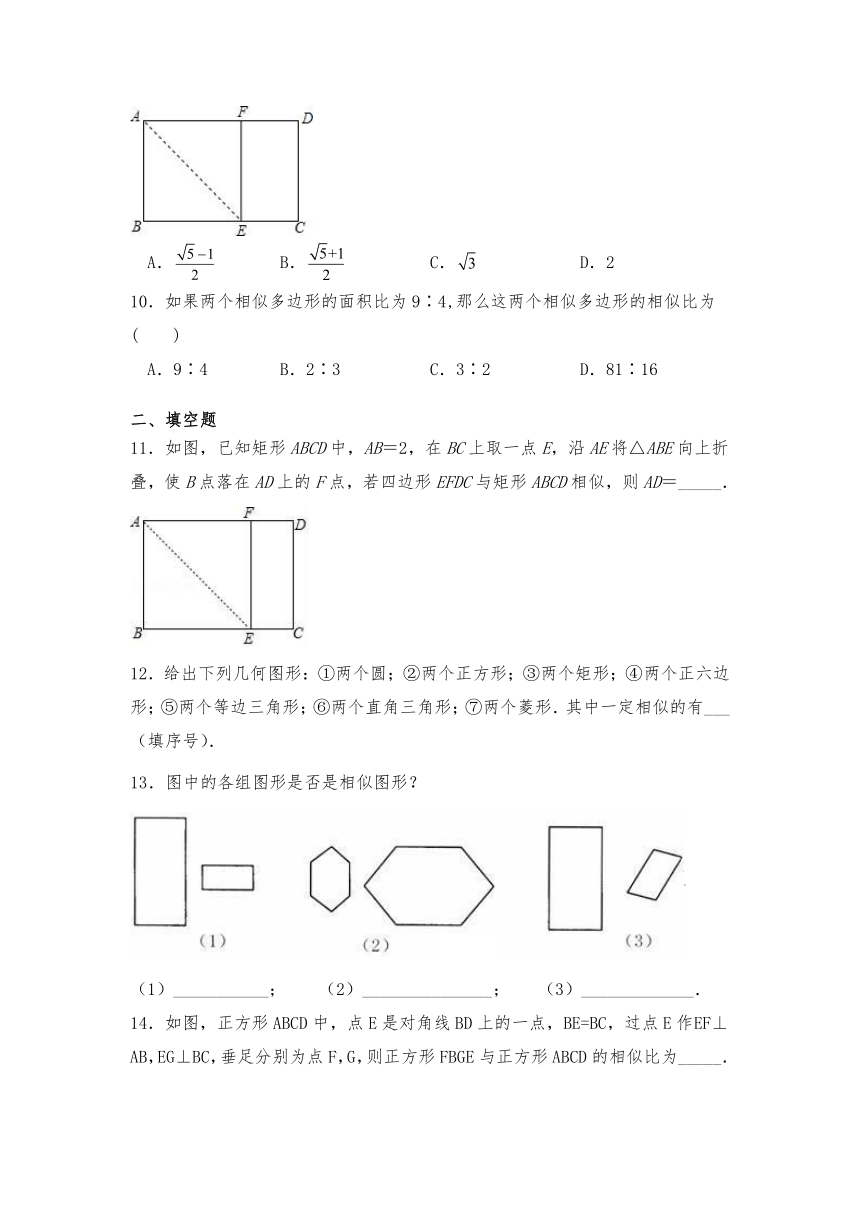
11.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=_____.
12.给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中一定相似的有___(填序号).
13.图中的各组图形是否是相似图形?
___________; (2)_______________; (3)_____________.
14.如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为_____.
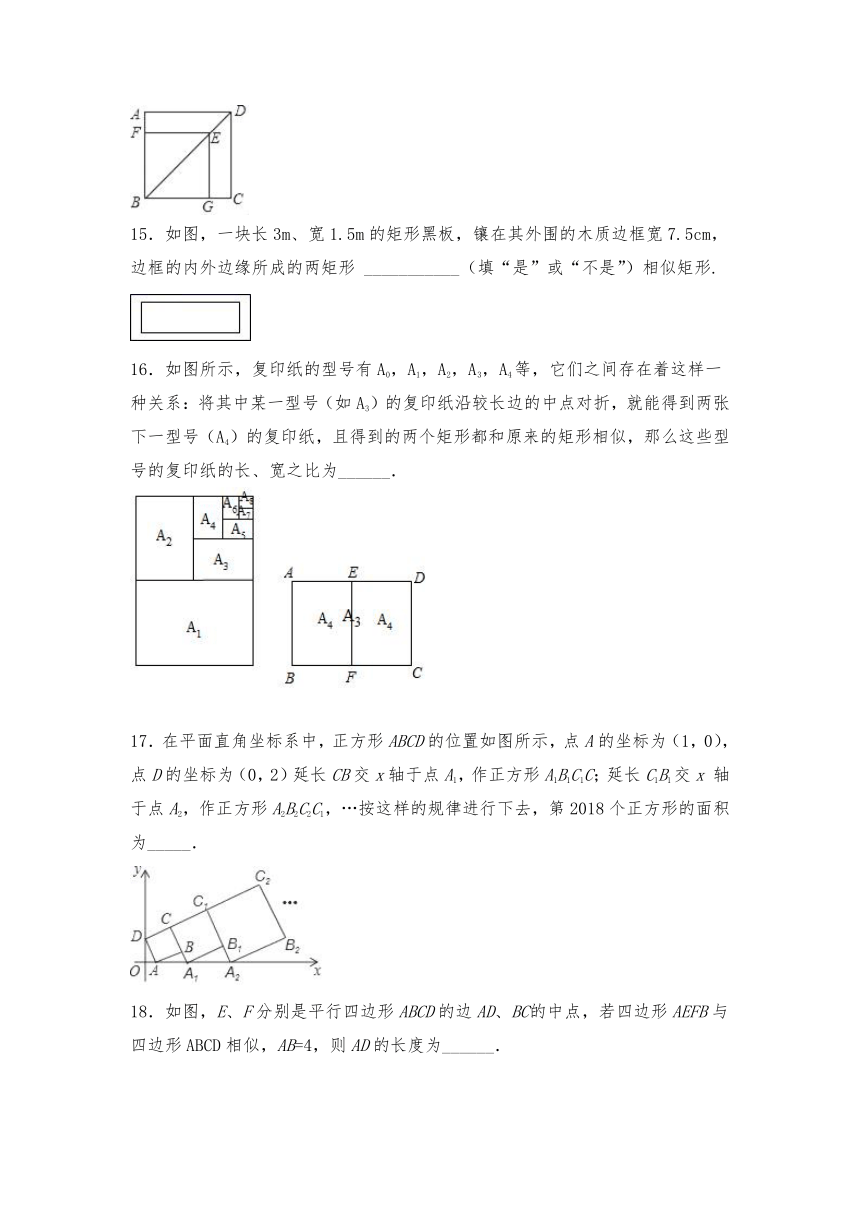
15.如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的两矩形 ___________(填“是”或“不是”)相似矩形.
16.如图所示,复印纸的型号有A0,A1,A2,A3,A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为______.
17.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2)延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为_____.
18.如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形ABCD相似,AB=4,则AD的长度为______.
三、解答题
19.我们已经知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.例如,两个正方形,它们的边长,对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形.请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.
20.如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2﹣4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
21.如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
22.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
23.如图,四边形与四边形相似,求的大小和的长度.
24.如图,四边形为平行四边形,平分交于点,过点作,交于点,连接.
(1)求证:平分;
(2)若,四边形与四边形相似,求的长.
25.已知四边形ABCD和A1B1C1D1中,,且周长之差为12cm,两个四边形的周长分别是多少?
26.如图,四边形ABCD∽四边形A′B′C′D′.
(1)α=
(2)求边x、y的长度.
答案
一、单选题
D.D.D.A.B.C.B.C.B.C.
二、填空题
11.1+
12.①②④⑤.
13.相似 相似 不相似
14.
15.不是.
16.
17.5×()2017.
18..
三、解答题
19.①两个圆,它们的所有元素都对应成比例,是相似图形;
②两个菱形,边的比一定相等,而对应角不一定对应相等,不一定是相似图形;
③两个长方形,对应角的度数一定相同,但对应边的比值不一定相等,不一定是相似图形;
④两个正六边形,它们的边长等元素对应成比例,对应角相等,是相似图形.
∴①④是相似图形,②③不一定是相似图形.
20.∵相似五边形的面积比是1:4,
∴它们的相似比为1:2,
即(x2﹣4):(x2+2x)=1:2,
整理得x2﹣2x﹣8=0,解得x1=4,x2=﹣2(舍去),
当x=4时,x2﹣4=12,x2+2x=24,
∴这根铁丝的总长=5×12+5×24=180(cm).
21.解:∵矩形ABFE∽矩形DEFC,且相似比为1:2,
∴ ,
∵四边形ABCD为矩形,
∴CD=AB=4
∴,
∴DE=8,AE=2,
∴AD=AE+DE=2+8=10.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC;
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴ ,即,
解得:BC=3±3(负值舍去),
∴BC=3+3.
23.解:∵四边形与四边形相似,
.
在四边形中,.
∵四边形与四边形相似,
,
解得
24.解:(1)证明:∵四边形是平行四边形,
,
又,
∴四边形是平行四边形.
由,
得.
平分
,
∴四边形是菱形,
平分.
(2)解:由(1)知,四边形为菱形,
.
∵四边形与四边形相似,
,
即,
或BC=(不符合实际,故舍去).
25.解:设四边形ABCD和四边形A1B1C1D1的周长分别为C1和C2,∵,
∴=
∴C1=C2
∵C2-C1=12
∴C2-C2=12
∴C2=30
∴C1=18
故两个四边形的周长分别为18cm和30cm.
26.解:(1)∵四边形ABCD∽四边形A′B′C′D′,
∴∠A=∠A′=62°,∠B=∠B′=75°,
∴α=360°﹣62°﹣75°﹣140°=83°,
故答案为83°;
(2)∵四边形ABCD∽四边形A′B′C′D′,
∴==,
解得:x=12,y=.
一、单选题
1.下列选项中的两个图形一定相似的是. ( )
A.两个等腰三角形 B.两个矩形 C.两个菱形 D.两个正五边形.
2.下列选项中,不是依据三角形全等知识解决问题的是( )
A.同一时刻,同一地点两栋等高建筑物影子一样长
B.工人师傅用角尺平分任意角
C.利用尺规作图,作一个角等于已知角
D.用放大镜观察蚂蚁的触角
3.在如图所示的图形中,形状相同的是( )
A.图①与图② B.图②与图③ C.图②与图④ D.图①与图④
4.用同一张底片洗出两张照片,一张为2寸,另一张为6寸,则这两张照片上的图像的大小比例为( )
A. B. C. D.不能确定
5.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则的值为( )
A. B. C. D.
6.在研究相似问题时,甲、乙两同学的观点如下:
甲:将边长为4的菱形按图1的方式向外扩张,得到新菱形,它们的对应边间距为1,则新菱形与原菱形相似.
乙:将边长为4的菱形按图2方式向外扩张,得到新菱形,每条对角线向其延长线两个方向各延伸1,则新菱形与原菱形相似;
对于两人的观点,下列说法正确的是( ).
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
7.如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是( )
A.28cm2 B.27cm2 C.21cm2 D.20cm2
8.如图所示的两个四边形相似,则α的度数是( )
A.60° B.75° C.87° D.120°
9.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将ΔABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).
A. B. C. D.2
10.如果两个相似多边形的面积比为9∶4,那么这两个相似多边形的相似比为( )
A.9∶4 B.2∶3 C.3∶2 D.81∶16
二、填空题
11.如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=_____.
12.给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中一定相似的有___(填序号).
13.图中的各组图形是否是相似图形?
___________; (2)_______________; (3)_____________.
14.如图,正方形ABCD中,点E是对角线BD上的一点,BE=BC,过点E作EF⊥AB,EG⊥BC,垂足分别为点F,G,则正方形FBGE与正方形ABCD的相似比为_____.
15.如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的两矩形 ___________(填“是”或“不是”)相似矩形.
16.如图所示,复印纸的型号有A0,A1,A2,A3,A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸沿较长边的中点对折,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似,那么这些型号的复印纸的长、宽之比为______.
17.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2)延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为_____.
18.如图,E、F分别是平行四边形ABCD的边AD、BC的中点,若四边形AEFB与四边形ABCD相似,AB=4,则AD的长度为______.
三、解答题
19.我们已经知道:如果两个几何图形形状相同而大小不一定相同,我们就把它们叫做相似图形.例如,两个正方形,它们的边长,对角线等所有元素都对应成比例,就可以称它们为相似图形.现给出下列4对几何图形:①两个圆;②两个菱形;③两个长方形;④两个正六边形.请指出其中哪几对是相似图形,哪几对不是相似图形,并简单地说明理由.
20.如图,如图用一根铁丝分成两段可以分别围成两个相似的五边形,已知它们的面积比是1:4,其中小五边形的边长为(x2﹣4)cm,大五边形的边长为(x2+2x)cm(其中x>0).求这这根铁丝的总长.
21.如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
22.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
23.如图,四边形与四边形相似,求的大小和的长度.
24.如图,四边形为平行四边形,平分交于点,过点作,交于点,连接.
(1)求证:平分;
(2)若,四边形与四边形相似,求的长.
25.已知四边形ABCD和A1B1C1D1中,,且周长之差为12cm,两个四边形的周长分别是多少?
26.如图,四边形ABCD∽四边形A′B′C′D′.
(1)α=
(2)求边x、y的长度.
答案
一、单选题
D.D.D.A.B.C.B.C.B.C.
二、填空题
11.1+
12.①②④⑤.
13.相似 相似 不相似
14.
15.不是.
16.
17.5×()2017.
18..
三、解答题
19.①两个圆,它们的所有元素都对应成比例,是相似图形;
②两个菱形,边的比一定相等,而对应角不一定对应相等,不一定是相似图形;
③两个长方形,对应角的度数一定相同,但对应边的比值不一定相等,不一定是相似图形;
④两个正六边形,它们的边长等元素对应成比例,对应角相等,是相似图形.
∴①④是相似图形,②③不一定是相似图形.
20.∵相似五边形的面积比是1:4,
∴它们的相似比为1:2,
即(x2﹣4):(x2+2x)=1:2,
整理得x2﹣2x﹣8=0,解得x1=4,x2=﹣2(舍去),
当x=4时,x2﹣4=12,x2+2x=24,
∴这根铁丝的总长=5×12+5×24=180(cm).
21.解:∵矩形ABFE∽矩形DEFC,且相似比为1:2,
∴ ,
∵四边形ABCD为矩形,
∴CD=AB=4
∴,
∴DE=8,AE=2,
∴AD=AE+DE=2+8=10.
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC;
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴ ,即,
解得:BC=3±3(负值舍去),
∴BC=3+3.
23.解:∵四边形与四边形相似,
.
在四边形中,.
∵四边形与四边形相似,
,
解得
24.解:(1)证明:∵四边形是平行四边形,
,
又,
∴四边形是平行四边形.
由,
得.
平分
,
∴四边形是菱形,
平分.
(2)解:由(1)知,四边形为菱形,
.
∵四边形与四边形相似,
,
即,
或BC=(不符合实际,故舍去).
25.解:设四边形ABCD和四边形A1B1C1D1的周长分别为C1和C2,∵,
∴=
∴C1=C2
∵C2-C1=12
∴C2-C2=12
∴C2=30
∴C1=18
故两个四边形的周长分别为18cm和30cm.
26.解:(1)∵四边形ABCD∽四边形A′B′C′D′,
∴∠A=∠A′=62°,∠B=∠B′=75°,
∴α=360°﹣62°﹣75°﹣140°=83°,
故答案为83°;
(2)∵四边形ABCD∽四边形A′B′C′D′,
∴==,
解得:x=12,y=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
