等腰三角形(2)导学案
图片预览
文档简介
“136”导学案——八年级数学(上)
编号: 班级: 姓名:
课题:等腰三角形(2)
主备: 审核: 时间:2014年 9 月 日
一、学习目标
1、掌握等腰三角形的判定方法。
2、运用等腰三角形的判定进行证明和计算。
教学重、难点:
重点:等腰三角形的判定定理。
难点:等腰三角形的判定定理的证明。
二、自主预习
自学指导:阅读教材第77至78页,完成下列各题。
1、在△ABC中,若∠B=∠C,则_______=_______.
2、在△ABC中:
⑴若∠B=∠C,AB=5,则AC=_______.
⑵若∠B=50°,∠C=65°,则△ABC的形状是_______.
⑶若∠A:∠B:∠C=1:1:2,则△ABC的形状是_______.
3、在△ABC中:
⑴若两个内角分别为40°、100°,则这个三角形是_______三角形.
⑵若∠A:∠B:∠C=1:2:2,则这个三角形是_______三角形.
⑶若∠A=∠B,AC=3cm,则BC=_______.
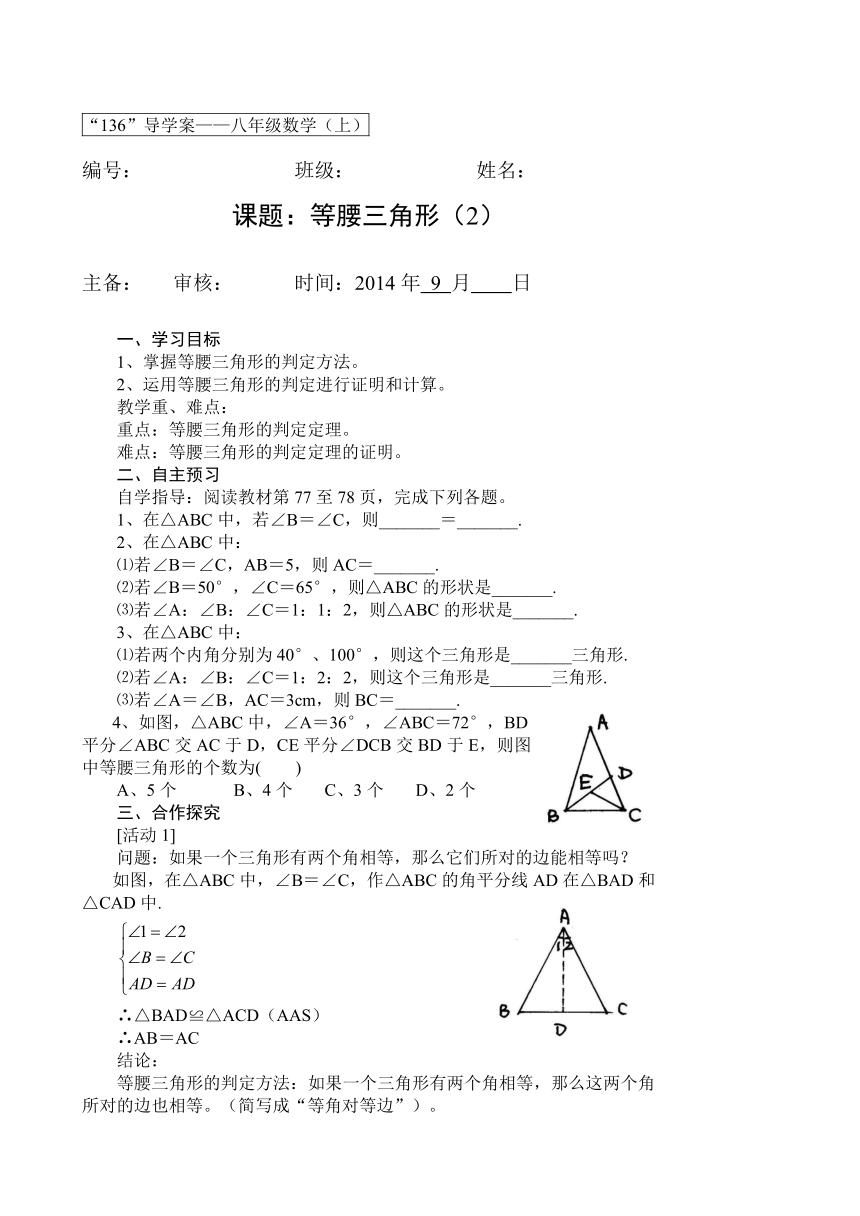
4、如图,△ABC中,∠A=36°,∠A ( http: / / www.21cnjy.com )BC=72°,BD平分∠ABC交AC于D,CE平分∠DCB交BD于E,则图中等腰三角形的个数为( )
A、5个 B、4个 C、3个 D、2个
三、合作探究
[活动1]
问题:如果一个三角形有两个角相等,那么它们所对的边能相等吗?
如图,在△ABC中,∠B=∠C,作△ABC的角平分线AD在△BAD和△CAD中.
∴△BAD≌△ACD(AAS)
∴AB=AC
结论:
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等。(简写成“等角对等边”)。
[活动2]
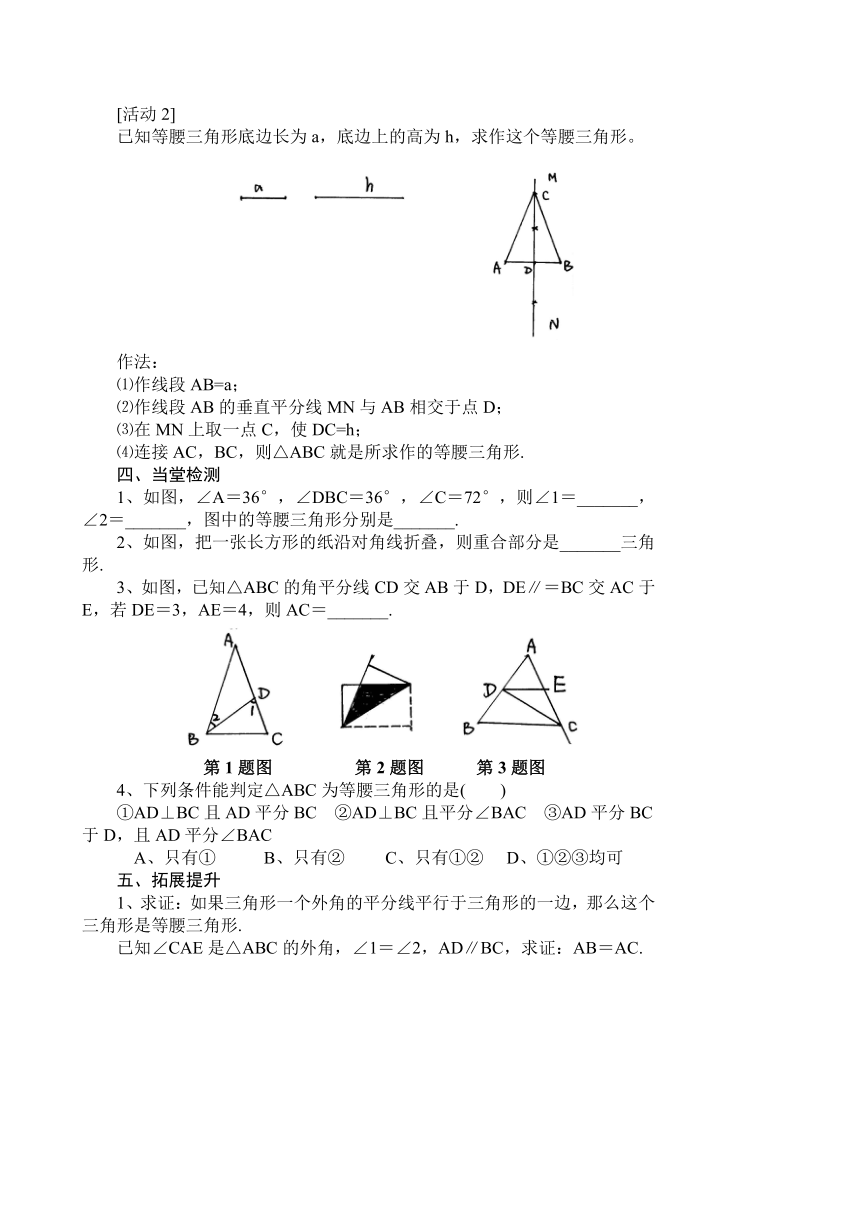
已知等腰三角形底边长为a,底边上的高为h,求作这个等腰三角形。
( http: / / www.21cnjy.com )
作法:
⑴作线段AB=a;
⑵作线段AB的垂直平分线MN与AB相交于点D;
⑶在MN上取一点C,使DC=h;
⑷连接AC,BC,则△ABC就是所求作的等腰三角形.
四、当堂检测
1、如图,∠A=36°,∠DBC=36°, ( http: / / www.21cnjy.com )∠C=72°,则∠1=_______,∠2=_______,图中的等腰三角形分别是_______.
2、如图,把一张长方形的纸沿对角线折叠,则重合部分是_______三角形.
3、如图,已知△ABC的角平分线CD交AB于D,DE∥=BC交AC于E,若DE=3,AE=4,则AC=_______.
( http: / / www.21cnjy.com )
第1题图 第2题图 第3题图
4、下列条件能判定△ABC为等腰三角形的是( )
①AD⊥BC且AD平分BC ②AD⊥BC且平分∠BAC ③AD平分BC于D,且AD平分∠BAC
A、只有① B、只有② C、只有①② D、①②③均可
五、拓展提升
1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知∠CAE是△ABC的外角,∠1=∠2,AD∥BC,求证:AB=AC.
2、如图,AC和BD相交于点O,且AB∥DC,OA=OB. 求证:OC=OD.
( http: / / www.21cnjy.com )
3、求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
六、课后作业
1、下列条件中不能说明三角形是等腰三角形的是( )
A、有两个内角是70°和40°的三角形
B、有一个角是45°的直角三角形
C、一外角为130°与它不相邻内角为50°的三角形
D、有两个角为70°和50°
2、如图,已知OC平分∠AOB,CD⊥OB,若OD=3cm,则CD=( )
A、3cm B、4cm C、1.5cm D、9cm
3、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
( http: / / www.21cnjy.com )
A、①②③ B、①②④ C、②③④ D、①③④
4、如图所示的正方形网格中,网格线的交点称 ( http: / / www.21cnjy.com )为格点,已知A、B是两格点,如果C是图中格点,且使得△ABC为等腰三角形,则点C的个数是( )
A、6个 B、7个 C、8个 D、9个
5、已知,点D到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
⑴如图①,若点O在边BC上,求证:AB=AC.
⑵如图②,若点O在△ABC的内部,求证:AB=AC.
⑶若点O在△ABC的外部,AB=AC成立吗?请画图表示.
( http: / / www.21cnjy.com )
七、课堂小结
学生总结,这节课学到了什么?
八、教学反思
编号: 班级: 姓名:
课题:等腰三角形(2)
主备: 审核: 时间:2014年 9 月 日
一、学习目标
1、掌握等腰三角形的判定方法。
2、运用等腰三角形的判定进行证明和计算。
教学重、难点:
重点:等腰三角形的判定定理。
难点:等腰三角形的判定定理的证明。
二、自主预习
自学指导:阅读教材第77至78页,完成下列各题。
1、在△ABC中,若∠B=∠C,则_______=_______.
2、在△ABC中:
⑴若∠B=∠C,AB=5,则AC=_______.
⑵若∠B=50°,∠C=65°,则△ABC的形状是_______.
⑶若∠A:∠B:∠C=1:1:2,则△ABC的形状是_______.
3、在△ABC中:
⑴若两个内角分别为40°、100°,则这个三角形是_______三角形.
⑵若∠A:∠B:∠C=1:2:2,则这个三角形是_______三角形.
⑶若∠A=∠B,AC=3cm,则BC=_______.
4、如图,△ABC中,∠A=36°,∠A ( http: / / www.21cnjy.com )BC=72°,BD平分∠ABC交AC于D,CE平分∠DCB交BD于E,则图中等腰三角形的个数为( )
A、5个 B、4个 C、3个 D、2个
三、合作探究
[活动1]
问题:如果一个三角形有两个角相等,那么它们所对的边能相等吗?
如图,在△ABC中,∠B=∠C,作△ABC的角平分线AD在△BAD和△CAD中.
∴△BAD≌△ACD(AAS)
∴AB=AC
结论:
等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的边也相等。(简写成“等角对等边”)。
[活动2]
已知等腰三角形底边长为a,底边上的高为h,求作这个等腰三角形。
( http: / / www.21cnjy.com )
作法:
⑴作线段AB=a;
⑵作线段AB的垂直平分线MN与AB相交于点D;
⑶在MN上取一点C,使DC=h;
⑷连接AC,BC,则△ABC就是所求作的等腰三角形.
四、当堂检测
1、如图,∠A=36°,∠DBC=36°, ( http: / / www.21cnjy.com )∠C=72°,则∠1=_______,∠2=_______,图中的等腰三角形分别是_______.
2、如图,把一张长方形的纸沿对角线折叠,则重合部分是_______三角形.
3、如图,已知△ABC的角平分线CD交AB于D,DE∥=BC交AC于E,若DE=3,AE=4,则AC=_______.
( http: / / www.21cnjy.com )
第1题图 第2题图 第3题图
4、下列条件能判定△ABC为等腰三角形的是( )
①AD⊥BC且AD平分BC ②AD⊥BC且平分∠BAC ③AD平分BC于D,且AD平分∠BAC
A、只有① B、只有② C、只有①② D、①②③均可
五、拓展提升
1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.
已知∠CAE是△ABC的外角,∠1=∠2,AD∥BC,求证:AB=AC.
2、如图,AC和BD相交于点O,且AB∥DC,OA=OB. 求证:OC=OD.
( http: / / www.21cnjy.com )
3、求证:如果三角形一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
六、课后作业
1、下列条件中不能说明三角形是等腰三角形的是( )
A、有两个内角是70°和40°的三角形
B、有一个角是45°的直角三角形
C、一外角为130°与它不相邻内角为50°的三角形
D、有两个角为70°和50°
2、如图,已知OC平分∠AOB,CD⊥OB,若OD=3cm,则CD=( )
A、3cm B、4cm C、1.5cm D、9cm
3、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
( http: / / www.21cnjy.com )
A、①②③ B、①②④ C、②③④ D、①③④
4、如图所示的正方形网格中,网格线的交点称 ( http: / / www.21cnjy.com )为格点,已知A、B是两格点,如果C是图中格点,且使得△ABC为等腰三角形,则点C的个数是( )
A、6个 B、7个 C、8个 D、9个
5、已知,点D到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
⑴如图①,若点O在边BC上,求证:AB=AC.
⑵如图②,若点O在△ABC的内部,求证:AB=AC.
⑶若点O在△ABC的外部,AB=AC成立吗?请画图表示.
( http: / / www.21cnjy.com )
七、课堂小结
学生总结,这节课学到了什么?
八、教学反思
