角平分线的判定 导学案
图片预览

文档简介
136导学案——八年级数学(上)
编号: 班级: 姓名:
课题:角平分线的判定
主备: 审核: 时间:2014年 月 第 周
一、教学目标:
1、掌握角平分线的判定方法
2、能够运用角平分线的性质和判定进行推理和计算
3、通过相关的数学活动,培养学生能力,激发学生的学习兴趣
教学重点:角平分线判定的证明及运用
教学难点:灵活运用角平分线的性质和判定解决问题
教学过程:
二、自主预习:
1、角的内部到角的两边的距离相等的点在_______上。
2、如图,∠A=∠C=90°,根据角平分线的判定填空。
1)若DA=DC,则∠_____=∠_______
2)若BA=BC,则∠_____=∠________
3、如图,DB⊥AB,DC⊥AC,BD=CD,∠BAC=80°,则∠BAD=____,∠ADC=_________.
4、到三角形三边距离相等的点( )
A、三条高所在直线的交点 B、三条中线的交点
C、三条角平分线的交点 D、不存在
5、如图,点P是∠BAC内一点,到AB、AC的距离PE=PF,则△PEA≌△PFA的理由是________________.
三、合作探究:
探索并证明角平分线的性质定理的逆定理:
(1)交换角的平分线的性质中的已知和结论,
你能得到什么结论,这个新结论正确吗?
[角的内部到角的两边距离相等的点在角的平分线上.]
(2)你能证明这个结论的正确性吗?(学生完成)
(3)这个结论与角的平分线的性质在应用上有
什么不同?
[这个结论可以判定角的平分线,而角的平分线的性质可用来证明线段相等.]
四、当堂评价:
1.判断题:
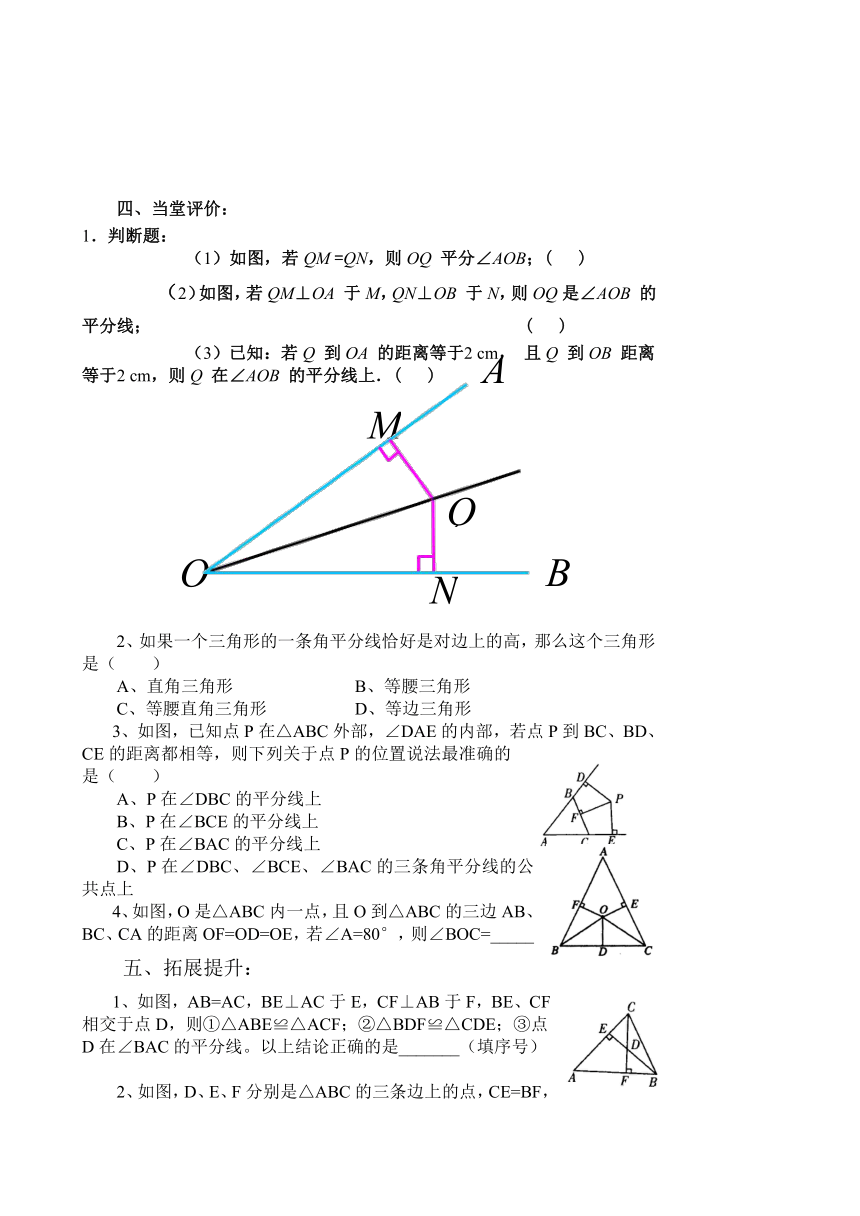
(1)如图,若QM =QN,则OQ 平分∠AOB;( )
(2)如图,若QM⊥OA 于M,QN⊥O ( http: / / www.21cnjy.com )B 于N,则OQ是∠AOB 的平分线; ( )
(3)已知:若Q ( http: / / www.21cnjy.com )到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )
2、如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形是( )
A、直角三角形 B、等腰三角形
C、等腰直角三角形 D、等边三角形
3、如图,已知点P在△ABC外部,∠DAE的内部,若点P到BC、BD、CE的距离都相等,则下列关于点P的位置说法最准确的是( )
A、P在∠DBC的平分线上
B、P在∠BCE的平分线上
C、P在∠BAC的平分线上
D、P在∠DBC、∠BCE、∠BAC的三条角平分线的公共点上
4、如图,O是△ABC内一点,且O到△ABC的三边AB、BC、CA的距离OF=OD=OE,若∠A=80°,则∠BOC=_____
五、拓展提升:
1、如图,AB=AC,BE⊥AC于E,CF ( http: / / www.21cnjy.com )⊥AB于F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线。以上结论正确的是_______(填序号)
2、如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△BDF的面积相等,求证:AD平分∠BAC.
( http: / / www.21cnjy.com )
3、如图,已知点P是△ABC中BC边的中点,PD⊥AB于D,PE⊥AC于E,
1)当PD=PE时,求证:AB=AC.
2)当AB=AC时,求证:PD=PE.
( http: / / www.21cnjy.com )
六、课后检测:
1、如图,AB∥CD,点P到AB、BC、CD的距离相等,则∠BPC=_____。
2、如图,AB=AD,∠A ( http: / / www.21cnjy.com )BC=∠ADC=90°,则下列结论①∠3=∠4;②∠1=∠2;③∠5=∠6;④AC垂直且平分BD,其中正确的有__________.
3、如图,Rt△ABC中,∠C=90°,D为BC上一点,DE⊥AB于点E,DE=DC,且E恰好为AB的中点,则∠B=_______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第1题图 第2题图 第3题图
4、如图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN的周长是__________.
5、如图,∠B=∠C=90°,点M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.
( http: / / www.21cnjy.com )
6、如图,已知AB=CD,△PAB和△PCD的面积相等,求证:OP平分∠AOC.
( http: / / www.21cnjy.com )
7、如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AB,AC=AE,
1)求证:△ACD≌△AEB.
2)试猜想∠AFD和∠AFE的大小关系,并证明你的结论。
( http: / / www.21cnjy.com )
七、课堂小结:这堂课学到了什么?(学生总结)
八、教学反思:
A
B
O
Q
M
N
编号: 班级: 姓名:
课题:角平分线的判定
主备: 审核: 时间:2014年 月 第 周
一、教学目标:
1、掌握角平分线的判定方法
2、能够运用角平分线的性质和判定进行推理和计算
3、通过相关的数学活动,培养学生能力,激发学生的学习兴趣
教学重点:角平分线判定的证明及运用
教学难点:灵活运用角平分线的性质和判定解决问题
教学过程:
二、自主预习:
1、角的内部到角的两边的距离相等的点在_______上。
2、如图,∠A=∠C=90°,根据角平分线的判定填空。
1)若DA=DC,则∠_____=∠_______
2)若BA=BC,则∠_____=∠________
3、如图,DB⊥AB,DC⊥AC,BD=CD,∠BAC=80°,则∠BAD=____,∠ADC=_________.
4、到三角形三边距离相等的点( )
A、三条高所在直线的交点 B、三条中线的交点
C、三条角平分线的交点 D、不存在
5、如图,点P是∠BAC内一点,到AB、AC的距离PE=PF,则△PEA≌△PFA的理由是________________.
三、合作探究:
探索并证明角平分线的性质定理的逆定理:
(1)交换角的平分线的性质中的已知和结论,
你能得到什么结论,这个新结论正确吗?
[角的内部到角的两边距离相等的点在角的平分线上.]
(2)你能证明这个结论的正确性吗?(学生完成)
(3)这个结论与角的平分线的性质在应用上有
什么不同?
[这个结论可以判定角的平分线,而角的平分线的性质可用来证明线段相等.]
四、当堂评价:
1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )
(2)如图,若QM⊥OA 于M,QN⊥O ( http: / / www.21cnjy.com )B 于N,则OQ是∠AOB 的平分线; ( )
(3)已知:若Q ( http: / / www.21cnjy.com )到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )
2、如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形是( )
A、直角三角形 B、等腰三角形
C、等腰直角三角形 D、等边三角形
3、如图,已知点P在△ABC外部,∠DAE的内部,若点P到BC、BD、CE的距离都相等,则下列关于点P的位置说法最准确的是( )
A、P在∠DBC的平分线上
B、P在∠BCE的平分线上
C、P在∠BAC的平分线上
D、P在∠DBC、∠BCE、∠BAC的三条角平分线的公共点上
4、如图,O是△ABC内一点,且O到△ABC的三边AB、BC、CA的距离OF=OD=OE,若∠A=80°,则∠BOC=_____
五、拓展提升:
1、如图,AB=AC,BE⊥AC于E,CF ( http: / / www.21cnjy.com )⊥AB于F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线。以上结论正确的是_______(填序号)
2、如图,D、E、F分别是△ABC的三条边上的点,CE=BF,△DCE和△BDF的面积相等,求证:AD平分∠BAC.
( http: / / www.21cnjy.com )
3、如图,已知点P是△ABC中BC边的中点,PD⊥AB于D,PE⊥AC于E,
1)当PD=PE时,求证:AB=AC.
2)当AB=AC时,求证:PD=PE.
( http: / / www.21cnjy.com )
六、课后检测:
1、如图,AB∥CD,点P到AB、BC、CD的距离相等,则∠BPC=_____。
2、如图,AB=AD,∠A ( http: / / www.21cnjy.com )BC=∠ADC=90°,则下列结论①∠3=∠4;②∠1=∠2;③∠5=∠6;④AC垂直且平分BD,其中正确的有__________.
3、如图,Rt△ABC中,∠C=90°,D为BC上一点,DE⊥AB于点E,DE=DC,且E恰好为AB的中点,则∠B=_______.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第1题图 第2题图 第3题图
4、如图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN的周长是__________.
5、如图,∠B=∠C=90°,点M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.
( http: / / www.21cnjy.com )
6、如图,已知AB=CD,△PAB和△PCD的面积相等,求证:OP平分∠AOC.
( http: / / www.21cnjy.com )
7、如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AB,AC=AE,
1)求证:△ACD≌△AEB.
2)试猜想∠AFD和∠AFE的大小关系,并证明你的结论。
( http: / / www.21cnjy.com )
七、课堂小结:这堂课学到了什么?(学生总结)
八、教学反思:
A
B
O
Q
M
N
