人教版八年级上册数学 11.3.1多边形 同步训练(含答案)
文档属性
| 名称 | 人教版八年级上册数学 11.3.1多边形 同步训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 119.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-05 20:54:07 | ||
图片预览

文档简介
人教版八年级上册数学11.3.1多边形同步训练
一、单选题
1.经过多边形的一个顶点的所有对角线把多边形分成3个三角形,则这个多边形是( )
A.七边形 B.六边形 C.五边形 D.四边形
2.从一个多边形的一个顶点出发,最多可画条对角线,则它是( )边形.
A. B. C. D.
3.一个正多边形的边长是3,从一个顶点可以引出4条对角线,则这个正多边形的周长是( )
A.12 B.15 C.18 D.21
4.过某个多边形一个顶点的所有对角线,将此多边形分成4个三角形,则此多边形的边数为( )
A.7 B.6 C.5 D.4
5.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
6.过边形的一个顶点有12条对角线,边形没有对角线,则的值为( )
A.27 B.30 C.36 D.45
7.从n边形的一个顶点出发作对角线,这些对角线把这个n边形分成的三角形个数为( )
A.(n+1)个 B.n个 C.(n﹣1)个 D.(n﹣2)个
8.如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( )
A.0<AD<7 B.2<AD<7 C.0<AD<13 D.1<AD<13
二、填空题
9.若从一个边形的一个顶点出发,最多可以引条对角线,则 ______ .
10.若从八边形的一个顶点出发,最多可以将此多边形分成________个三角形.
11.若一个多边形截去一个角后,得到的新多边形为十五边形,则原来的多边形边数为______.
12.过某多边形一个顶点的所有对角线,将这个多边形分成3个三角形,这个多边形的边数是______.
13.若一个多边形的边数是这个多边形从一个顶点发出的对角线条数的2倍,则这个多边形是 __边形.
14.一个正八边形,从它的一个顶点可引出m条对角线,并把这个正八边形分成n个三角形,则___________.
15.过边形的一个顶点可作对角线___________条,将多边形分为___________个三角形.
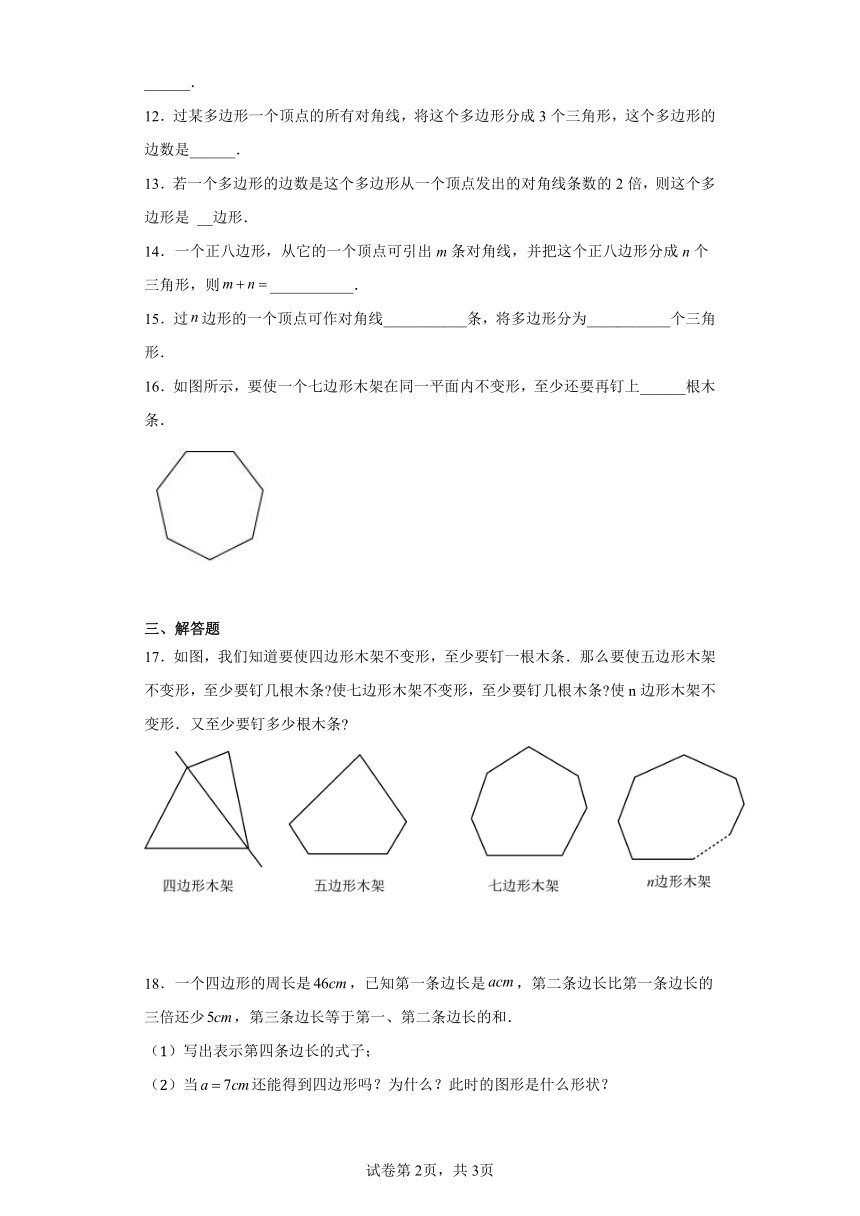
16.如图所示,要使一个七边形木架在同一平面内不变形,至少还要再钉上______根木条.
三、解答题
17.如图,我们知道要使四边形木架不变形,至少要钉一根木条.那么要使五边形木架不变形,至少要钉几根木条 使七边形木架不变形,至少要钉几根木条 使n边形木架不变形.又至少要钉多少根木条
18.一个四边形的周长是,已知第一条边长是,第二条边长比第一条边长的三倍还少,第三条边长等于第一、第二条边长的和.
(1)写出表示第四条边长的式子;
(2)当还能得到四边形吗?为什么?此时的图形是什么形状?
19.探究归纳题:
(1)试验分析:如图1,经过A点可以作1条对角线;同样,经过B点可以作______条对角线;经过C点可以作______条对角线;经过D点可以作______条对角线.通过以上分析和总结,图1共有______条对角线.
(2)拓展延伸:运用1的分析方法,可得:图2共有______条对角线;图3共有______条对角线;
(3)探索归纳:对于n边形,共有______条对角线.(用含n的式子表示)
(4)特例验证:十边形有______对角线.
试卷第2页,共3页
试卷第3页,共3页
参考答案:
1.C
2.C
3.D
4.B
5.C
6.D
7.D
8.D
9.12
10.
11.14或15或16
12.5
13.六
14.
15. / /
16.4
17.要使五边形木架不变形,至少要钉2根木条;使七边形木架不变形,至少要钉4根木条;使n边形木架不变形,至少要钉(n-3)根木条.
18.(1)第四条边长的式子是.(2)当不能得到四边形,此时的图形是线段.
19.(1)1、1、1、2;(2)5、9;(3);(4)35
答案第1页,共2页
答案第1页,共1页
一、单选题
1.经过多边形的一个顶点的所有对角线把多边形分成3个三角形,则这个多边形是( )
A.七边形 B.六边形 C.五边形 D.四边形
2.从一个多边形的一个顶点出发,最多可画条对角线,则它是( )边形.
A. B. C. D.
3.一个正多边形的边长是3,从一个顶点可以引出4条对角线,则这个正多边形的周长是( )
A.12 B.15 C.18 D.21
4.过某个多边形一个顶点的所有对角线,将此多边形分成4个三角形,则此多边形的边数为( )
A.7 B.6 C.5 D.4
5.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是( )
A.5或6 B.6或7 C.5或6或7 D.6或7或8
6.过边形的一个顶点有12条对角线,边形没有对角线,则的值为( )
A.27 B.30 C.36 D.45
7.从n边形的一个顶点出发作对角线,这些对角线把这个n边形分成的三角形个数为( )
A.(n+1)个 B.n个 C.(n﹣1)个 D.(n﹣2)个
8.如图所示,四边形ABCD是凸四边形,AB=2,BC=4,CD=7,则线段AD的取值范围为( )
A.0<AD<7 B.2<AD<7 C.0<AD<13 D.1<AD<13
二、填空题
9.若从一个边形的一个顶点出发,最多可以引条对角线,则 ______ .
10.若从八边形的一个顶点出发,最多可以将此多边形分成________个三角形.
11.若一个多边形截去一个角后,得到的新多边形为十五边形,则原来的多边形边数为______.
12.过某多边形一个顶点的所有对角线,将这个多边形分成3个三角形,这个多边形的边数是______.
13.若一个多边形的边数是这个多边形从一个顶点发出的对角线条数的2倍,则这个多边形是 __边形.
14.一个正八边形,从它的一个顶点可引出m条对角线,并把这个正八边形分成n个三角形,则___________.
15.过边形的一个顶点可作对角线___________条,将多边形分为___________个三角形.
16.如图所示,要使一个七边形木架在同一平面内不变形,至少还要再钉上______根木条.
三、解答题
17.如图,我们知道要使四边形木架不变形,至少要钉一根木条.那么要使五边形木架不变形,至少要钉几根木条 使七边形木架不变形,至少要钉几根木条 使n边形木架不变形.又至少要钉多少根木条
18.一个四边形的周长是,已知第一条边长是,第二条边长比第一条边长的三倍还少,第三条边长等于第一、第二条边长的和.
(1)写出表示第四条边长的式子;
(2)当还能得到四边形吗?为什么?此时的图形是什么形状?
19.探究归纳题:
(1)试验分析:如图1,经过A点可以作1条对角线;同样,经过B点可以作______条对角线;经过C点可以作______条对角线;经过D点可以作______条对角线.通过以上分析和总结,图1共有______条对角线.
(2)拓展延伸:运用1的分析方法,可得:图2共有______条对角线;图3共有______条对角线;
(3)探索归纳:对于n边形,共有______条对角线.(用含n的式子表示)
(4)特例验证:十边形有______对角线.
试卷第2页,共3页
试卷第3页,共3页
参考答案:
1.C
2.C
3.D
4.B
5.C
6.D
7.D
8.D
9.12
10.
11.14或15或16
12.5
13.六
14.
15. / /
16.4
17.要使五边形木架不变形,至少要钉2根木条;使七边形木架不变形,至少要钉4根木条;使n边形木架不变形,至少要钉(n-3)根木条.
18.(1)第四条边长的式子是.(2)当不能得到四边形,此时的图形是线段.
19.(1)1、1、1、2;(2)5、9;(3);(4)35
答案第1页,共2页
答案第1页,共1页
