三角形的稳定性 导学案
图片预览

文档简介
136导学案——八年级数学(上)
编号: 班级: 姓名:
课题:三角形的稳定性
主备: 审核: 时间:2014年 9 月 日
一、学习目标:
1、掌握三角形的高、中线、角平分线的定义中体现出来的性质。
2、会画三角形的高、中线、角平分线。
3、了解三角形的稳定性。
教学重、难点
重点:了解三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线。
难点:
1、三角形的角平分线与角平分线的区别,三角形的高与垂线的区别。
2、钝角三角形高的画法。
3、不同的三角形三条高的位置关系。
教学过程:
二、自主预习:
自学指导:阅读教材第6至7页,完成下列各题
( http: / / www.21cnjy.com )
三、合作探究:
活动1、自主探究
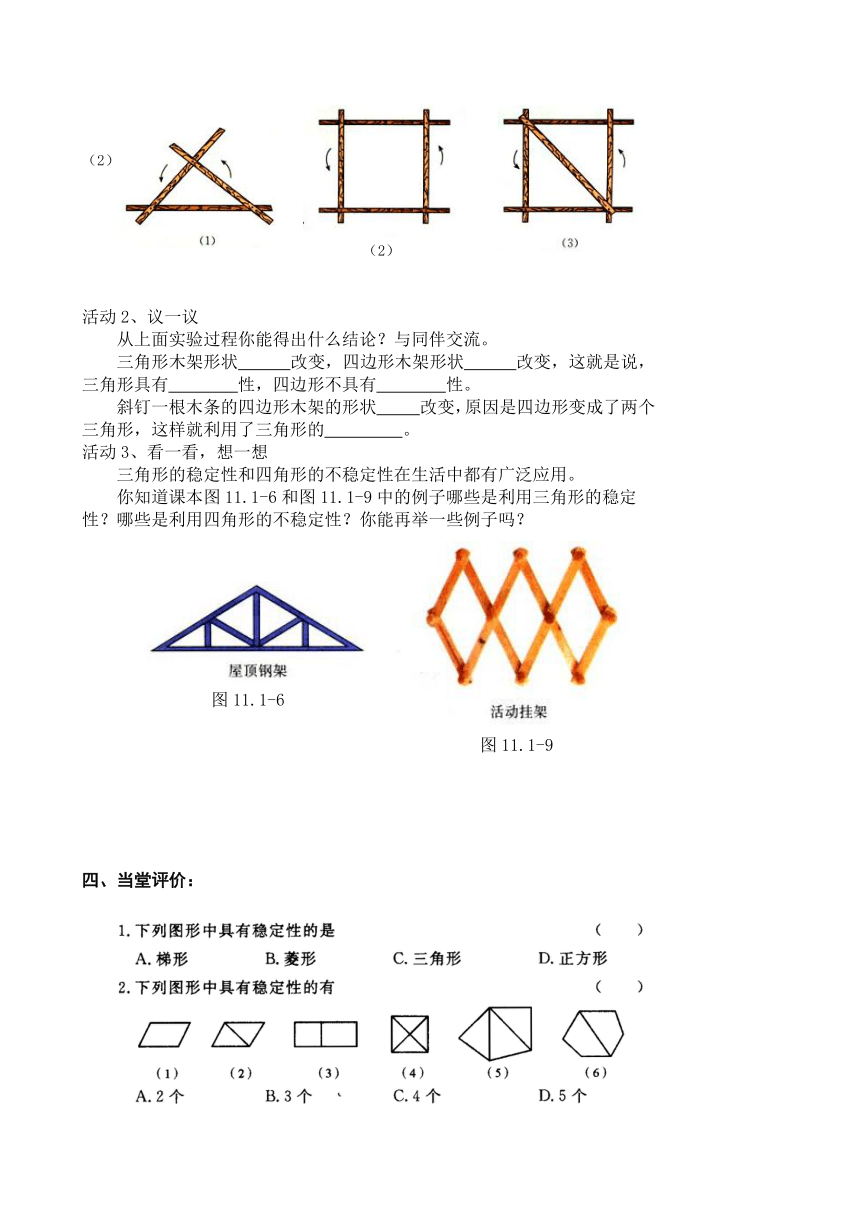
1、如图(1),用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
2、如图(2),用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3、如图(3),在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
(2)
(2)
活动2、议一议
从上面实验过程你能得出什么结论?与同伴交流。
三角形木架形状 改变,四边形木架形状 改变,这就是说,三角形具有 性,四边形不具有 性。
斜钉一根木条的四边形木架的形状 改变,原因是四边形变成了两个三角形,这样就利用了三角形的 。
活动3、看一看,想一想
三角形的稳定性和四角形的不稳定性在生活中都有广泛应用。
你知道课本图11.1-6和图11.1-9中的例子哪些是利用三角形的稳定性?哪些是利用四角形的不稳定性?你能再举一些例子吗?
图11.1-6
图11.1-9
四、当堂评价:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
五、拓展提升:
1、下列图形中具有稳定性的有
(1) (2) (3)
(4) (5) (6)
2、三角形具有稳定性,而其它多边形不具有 ( http: / / www.21cnjy.com )稳定性,要使多边形也具有稳定性必须额外加一些线段,将其转化为几个三角形。试探究要使四边形不变形,至少需要加 条线段,五边形至少需要加 条线段,六边形至少需要加 条线段,n边形(n﹥3)最少需要 条线段才具有稳定性。
3、在建筑工地我们常可看见如右图所示,用木条EF
固定矩形门框ABCD的情形.这种做法根据( )
A.两点之间线段最短 B.两点确定一条直线
C.三角形的稳定性 D.垂线段最短
4、下列图形具有稳定性的有( )
A.梯形 B. 长方形 C. 直角三角形 D. 正方形
六、课后检测:
( http: / / www.21cnjy.com )
4、如右图,一扇窗户打开后,用窗钩BC可将其固定,
这里所运用的几何原理是_____ ____。
5、我们学校的大门是电动推拉门,这种门工作的原理
是根据四边形的 。
七、课堂小结:学生总结,这节课学到了什么?
八、教学反思:
编号: 班级: 姓名:
课题:三角形的稳定性
主备: 审核: 时间:2014年 9 月 日
一、学习目标:
1、掌握三角形的高、中线、角平分线的定义中体现出来的性质。
2、会画三角形的高、中线、角平分线。
3、了解三角形的稳定性。
教学重、难点
重点:了解三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线。
难点:
1、三角形的角平分线与角平分线的区别,三角形的高与垂线的区别。
2、钝角三角形高的画法。
3、不同的三角形三条高的位置关系。
教学过程:
二、自主预习:
自学指导:阅读教材第6至7页,完成下列各题
( http: / / www.21cnjy.com )
三、合作探究:
活动1、自主探究
1、如图(1),用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
2、如图(2),用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3、如图(3),在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
(2)
(2)
活动2、议一议
从上面实验过程你能得出什么结论?与同伴交流。
三角形木架形状 改变,四边形木架形状 改变,这就是说,三角形具有 性,四边形不具有 性。
斜钉一根木条的四边形木架的形状 改变,原因是四边形变成了两个三角形,这样就利用了三角形的 。
活动3、看一看,想一想
三角形的稳定性和四角形的不稳定性在生活中都有广泛应用。
你知道课本图11.1-6和图11.1-9中的例子哪些是利用三角形的稳定性?哪些是利用四角形的不稳定性?你能再举一些例子吗?
图11.1-6
图11.1-9
四、当堂评价:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
五、拓展提升:
1、下列图形中具有稳定性的有
(1) (2) (3)
(4) (5) (6)
2、三角形具有稳定性,而其它多边形不具有 ( http: / / www.21cnjy.com )稳定性,要使多边形也具有稳定性必须额外加一些线段,将其转化为几个三角形。试探究要使四边形不变形,至少需要加 条线段,五边形至少需要加 条线段,六边形至少需要加 条线段,n边形(n﹥3)最少需要 条线段才具有稳定性。
3、在建筑工地我们常可看见如右图所示,用木条EF
固定矩形门框ABCD的情形.这种做法根据( )
A.两点之间线段最短 B.两点确定一条直线
C.三角形的稳定性 D.垂线段最短
4、下列图形具有稳定性的有( )
A.梯形 B. 长方形 C. 直角三角形 D. 正方形
六、课后检测:
( http: / / www.21cnjy.com )
4、如右图,一扇窗户打开后,用窗钩BC可将其固定,
这里所运用的几何原理是_____ ____。
5、我们学校的大门是电动推拉门,这种门工作的原理
是根据四边形的 。
七、课堂小结:学生总结,这节课学到了什么?
八、教学反思:
