多边形的内角和
图片预览

文档简介
136导学案——八年级数学(上)
编号: 班级: 姓名:
课题:多边形的内角和
主备: 审核: 时间:2014年 9 月 日
一、学习目标:
1、掌握多边形外角和及内角和公式。
2、通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法。
教学重、难点
重点:探索多边形的内角和公式及外角和。
难点:如何把多边形转化成三角形,用分割多边形法推导多边形的内角和与外角和。
教学过程:
二、自主预习:
自学指导:阅读教材第21至23页,完成下列各题。
( http: / / www.21cnjy.com )
三、合作探究:
1、 如果一个四边形的一组对角互补,那么另一组对角有什么关系
( http: / / www.21cnjy.com )
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
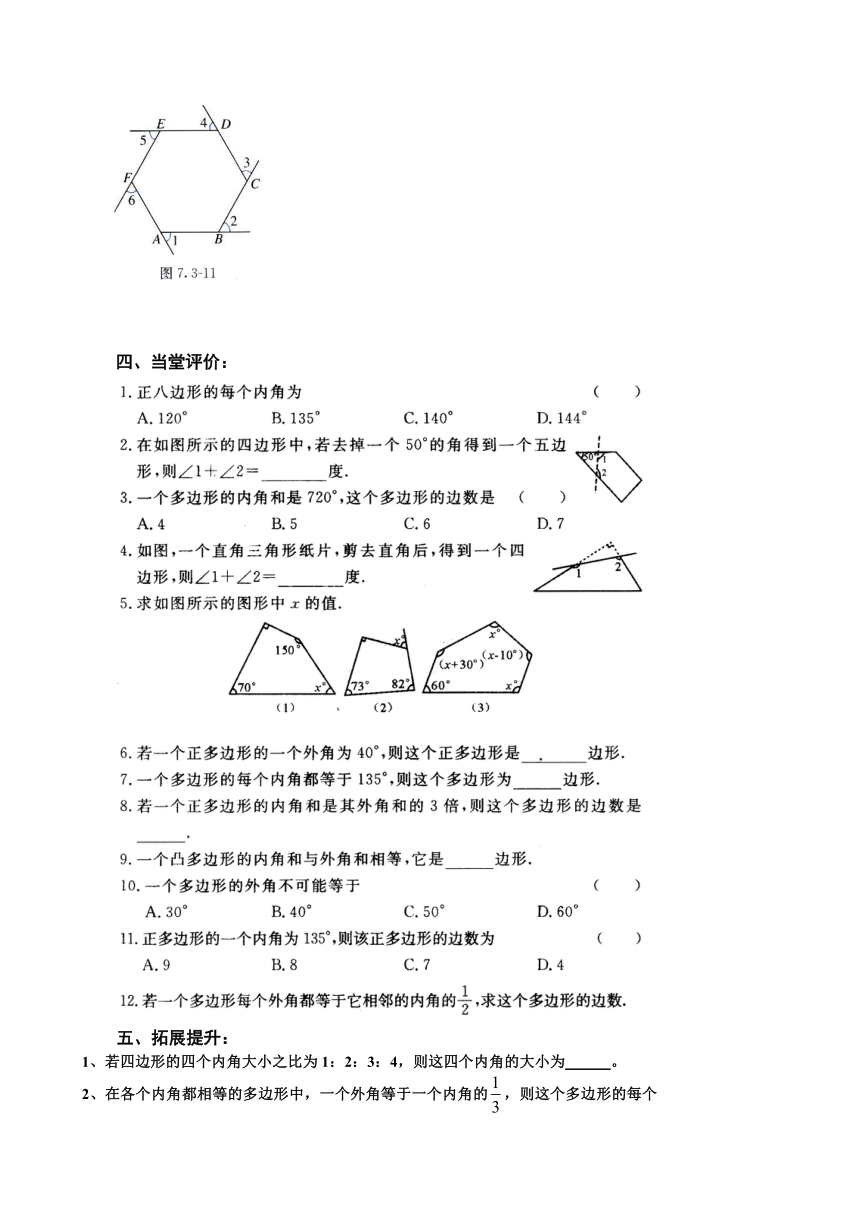
2、如图7.3—11,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少
( http: / / www.21cnjy.com )
四、当堂评价:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
五、拓展提升:
1、若四边形的四个内角大小之比为1:2:3:4,则这四个内角的大小为 。
2、在各个内角都相等的多边形中,一个外角等于一个内角的,则这个多边形的每个内角为 度。
3、若多边形内角和分别为下列度数时,试分别求出多边形的边数。
1260° ② 2160°
4、已知n边形的内角和与外角和之比为9:2,求n。
六、课后检测:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
七、课堂小结:学生总结,这节课学到了什么?
八、教学反思:
编号: 班级: 姓名:
课题:多边形的内角和
主备: 审核: 时间:2014年 9 月 日
一、学习目标:
1、掌握多边形外角和及内角和公式。
2、通过把多边形转化为三角形,体会转化思想在几何中的运用,让学生体会从特殊到一般的认识问题的方法。
教学重、难点
重点:探索多边形的内角和公式及外角和。
难点:如何把多边形转化成三角形,用分割多边形法推导多边形的内角和与外角和。
教学过程:
二、自主预习:
自学指导:阅读教材第21至23页,完成下列各题。
( http: / / www.21cnjy.com )
三、合作探究:
1、 如果一个四边形的一组对角互补,那么另一组对角有什么关系
( http: / / www.21cnjy.com )
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
2、如图7.3—11,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和。六边形的外角和等于多少
( http: / / www.21cnjy.com )
四、当堂评价:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
五、拓展提升:
1、若四边形的四个内角大小之比为1:2:3:4,则这四个内角的大小为 。
2、在各个内角都相等的多边形中,一个外角等于一个内角的,则这个多边形的每个内角为 度。
3、若多边形内角和分别为下列度数时,试分别求出多边形的边数。
1260° ② 2160°
4、已知n边形的内角和与外角和之比为9:2,求n。
六、课后检测:
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
七、课堂小结:学生总结,这节课学到了什么?
八、教学反思:
