2023-2024学年北师大版九年级数学上册课件:第一章第一节菱形的性质与判定(一)(28张PPT)
文档属性
| 名称 | 2023-2024学年北师大版九年级数学上册课件:第一章第一节菱形的性质与判定(一)(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 18:22:45 | ||
图片预览




文档简介
(共28张PPT)
第一章 特殊平行四边形
菱形的性质与判定(一)
思维导图
(限时3分钟)
温故知新
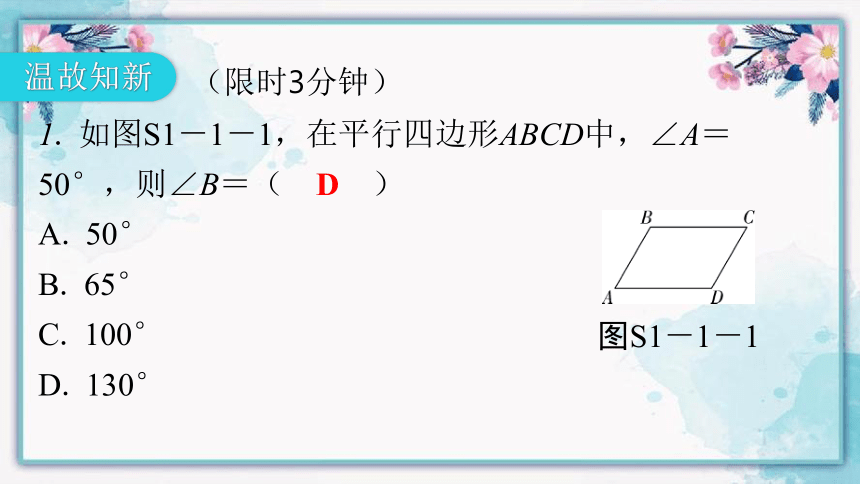
1. 如图S1-1-1,在平行四边形ABCD中,∠A=50°,则∠B=( D )
图S1-1-1
D
A. 50°
B. 65°
C. 100°
D. 130°
2. (2022广东)如图S1-1-2,在 ABCD中,一定正确的是( C )
图S1-1-2
C
A. AD=CD
B. AC=BD
C. AB=CD
D. CD=BC
知识重点
A. 有一组 邻边相等 的平行四边形叫做菱形.
邻边相等
对点范例
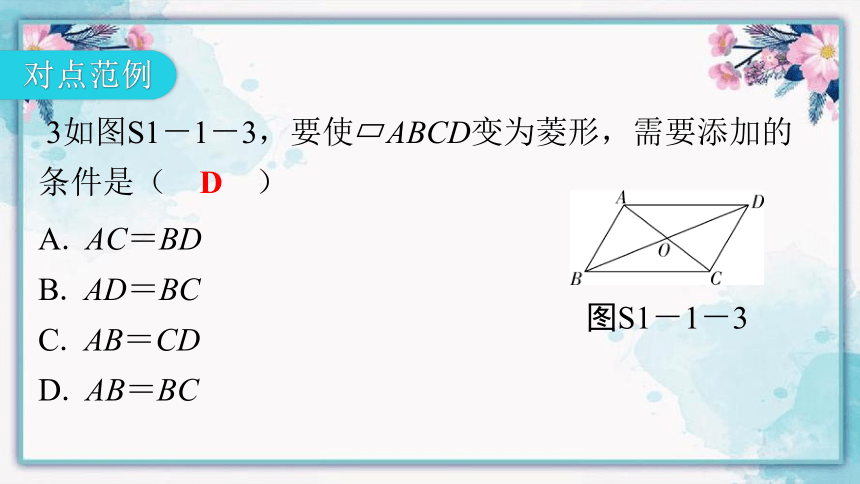
3如图S1-1-3,要使 ABCD变为菱形,需要添加的条件是( D )
图S1-1-3
D
A. AC=BD
B. AD=BC
C. AB=CD
D. AB=BC
知识重点
B. (1)菱形的四条边 相等 ;
(2)菱形的对角线 互相垂直 .
相等
互相垂直
对点范例
4如图S1-1-4,四边形ABCD是菱形,AD=BD,AD=2,则该菱形的周长与对角线AC的长分别是( D )
图S1-1-4
D
A. 16,4
B. 16,
C. 8,2
D. 8,2
课本母题
知识点1 菱形定义的应用
【例1】如图S1-1-5,在平行四边形ABCD中,已知AB=(2x-1)cm,BC=(x+2)cm.要使平行四边形ABCD变为菱形,则x的值应为多少?并求出此时菱形ABCD的边长.
图S1-1-5
思路点拨:当AB=BC时,平行四边形ABCD是菱形,列方程即可求出x 的值,进而可求出AB的长.
解:当AB=BC时,平行四边形ABCD是菱形,
∴2x-1=x+2.
解得x=3.
此时菱形ABCD的边AB长为x+2=5.
∴当x=3时,平行四边形ABCD是菱形,
此时菱形ABCD的边AB长为5 cm.
图S1-1-5
母题变式
5. (原创题)如图S1-1-6,平行四边形ABCD的两边AB,AD的长是关于x,y的方程组的解.当m为何值时,平行四边形ABCD是菱形?
求出这时菱形的边长.
图S1-1-6
解:
图S1-1-6
②-①得x=6-m.
把x=6-m代入①得y=2m-6.
则方程组的解为
∴当x=y时,平行四边形ABCD是菱形.
∴6-m=2m-6.解得m=4.
这时菱形的边长AB=6-m=6-4=2.
课本母题
知识点2 菱形的性质的运用(对角线与边长)
【例2】(课本P4随堂练习改编)如图S1-1-7,在菱形ABCD中,对角线AC与BD相交于点O.
已知AB=5 cm,BD=8 cm,求AC的长.
图S1-1-7
思路点拨:根据菱形的性质可得AC⊥DB,BO=BD,AO=AC,再利用勾股定理计算出AO的长,进而得到AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,BO=BD,AO=AC.
∵BD=8 cm,∴BO=4 cm.
在Rt△ABO中,AO==3(cm).
∴AC=2AO=6(cm).
图S1-1-7
母题变式
6. 如图S1-1-8,在菱形ABCD中,对角线AC,BD相交于点O,AB=5 cm,AO=4 cm.求:
图S1-1-8
(1)两条对角线AC和BD的长;
解:(1)∵四边形ABCD为菱形,
对角线AC,BD相交于点O,
∴AC⊥BD.
∵AB=5 cm,AO=4 cm,
在Rt△AOB中,BO==3(cm).
∴AC=2AO=8(cm),BD=2BO=6(cm).
图S1-1-8
(2)菱形ABCD的周长.
解:(2)菱形ABCD的周长为5×4=20(cm).
图S1-1-8
创新设计
7. (创新题)如图S1-1-9,在菱形ABCD中,对角线AC,BD相交于点O,E,F在对角线BD上,且BF=DE,连接AE,AF.
图S1-1-9
(1)求证:AE=AF;
(1)证明:∵四边形ABCD是菱形,
∴OB=OD,AC⊥BD.
∵BF=DE,
∴BF-OB=DE-OD,
即OF=OE.∴AE=AF.
图S1-1-9
(2)若BE=AE,BD=2AC=16,求线段EF的长.
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC.
∵BD=2AC=16,∴OA=4,OB=8.
设BE=AE=x,则OE=OB-BE=8-x.
在Rt△AOE中,AE2=OA2+OE2,即x2=(8-x)2+42.解得x=5.∴OE=8-5=3.由(1)知OF=OE,
∴EF=2OE=6.
图S1-1-9
8. (创新变式)如图S1-1-10,已知四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
图S1-1-10
(1)求证:AM=DM;
∴BD⊥AC,AB∥CD.∵EF⊥AC,∴EF∥BD.
∴四边形EFDB是平行四边形.
∴DF=EB.∵E是AB的中点,
∴AE=EB.∴AE=DF.
∵AB∥CD,∴∠EAM=∠FDM.
(1)证明:如答图S1-1-1,连接BD.
∵四边形ABCD是菱形,
答图S1-1-1
在△AME和△DMF中,
∴△AME≌△DMF(AAS).
∴AM=DM.
答图S1-1-1
(2)若DF=3,求菱形ABCD的周长.
图S1-1-10
(2)解:由(1)知△AME≌△DMF,
∴AE=DF=3.
∵E为AB的中点,∴AB=2AE=6.
∴菱形ABCD的周长为6×4=24.
谢 谢!
第一章 特殊平行四边形
菱形的性质与判定(一)
思维导图
(限时3分钟)
温故知新
1. 如图S1-1-1,在平行四边形ABCD中,∠A=50°,则∠B=( D )
图S1-1-1
D
A. 50°
B. 65°
C. 100°
D. 130°
2. (2022广东)如图S1-1-2,在 ABCD中,一定正确的是( C )
图S1-1-2
C
A. AD=CD
B. AC=BD
C. AB=CD
D. CD=BC
知识重点
A. 有一组 邻边相等 的平行四边形叫做菱形.
邻边相等
对点范例
3如图S1-1-3,要使 ABCD变为菱形,需要添加的条件是( D )
图S1-1-3
D
A. AC=BD
B. AD=BC
C. AB=CD
D. AB=BC
知识重点
B. (1)菱形的四条边 相等 ;
(2)菱形的对角线 互相垂直 .
相等
互相垂直
对点范例
4如图S1-1-4,四边形ABCD是菱形,AD=BD,AD=2,则该菱形的周长与对角线AC的长分别是( D )
图S1-1-4
D
A. 16,4
B. 16,
C. 8,2
D. 8,2
课本母题
知识点1 菱形定义的应用
【例1】如图S1-1-5,在平行四边形ABCD中,已知AB=(2x-1)cm,BC=(x+2)cm.要使平行四边形ABCD变为菱形,则x的值应为多少?并求出此时菱形ABCD的边长.
图S1-1-5
思路点拨:当AB=BC时,平行四边形ABCD是菱形,列方程即可求出x 的值,进而可求出AB的长.
解:当AB=BC时,平行四边形ABCD是菱形,
∴2x-1=x+2.
解得x=3.
此时菱形ABCD的边AB长为x+2=5.
∴当x=3时,平行四边形ABCD是菱形,
此时菱形ABCD的边AB长为5 cm.
图S1-1-5
母题变式
5. (原创题)如图S1-1-6,平行四边形ABCD的两边AB,AD的长是关于x,y的方程组的解.当m为何值时,平行四边形ABCD是菱形?
求出这时菱形的边长.
图S1-1-6
解:
图S1-1-6
②-①得x=6-m.
把x=6-m代入①得y=2m-6.
则方程组的解为
∴当x=y时,平行四边形ABCD是菱形.
∴6-m=2m-6.解得m=4.
这时菱形的边长AB=6-m=6-4=2.
课本母题
知识点2 菱形的性质的运用(对角线与边长)
【例2】(课本P4随堂练习改编)如图S1-1-7,在菱形ABCD中,对角线AC与BD相交于点O.
已知AB=5 cm,BD=8 cm,求AC的长.
图S1-1-7
思路点拨:根据菱形的性质可得AC⊥DB,BO=BD,AO=AC,再利用勾股定理计算出AO的长,进而得到AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD,BO=BD,AO=AC.
∵BD=8 cm,∴BO=4 cm.
在Rt△ABO中,AO==3(cm).
∴AC=2AO=6(cm).
图S1-1-7
母题变式
6. 如图S1-1-8,在菱形ABCD中,对角线AC,BD相交于点O,AB=5 cm,AO=4 cm.求:
图S1-1-8
(1)两条对角线AC和BD的长;
解:(1)∵四边形ABCD为菱形,
对角线AC,BD相交于点O,
∴AC⊥BD.
∵AB=5 cm,AO=4 cm,
在Rt△AOB中,BO==3(cm).
∴AC=2AO=8(cm),BD=2BO=6(cm).
图S1-1-8
(2)菱形ABCD的周长.
解:(2)菱形ABCD的周长为5×4=20(cm).
图S1-1-8
创新设计
7. (创新题)如图S1-1-9,在菱形ABCD中,对角线AC,BD相交于点O,E,F在对角线BD上,且BF=DE,连接AE,AF.
图S1-1-9
(1)求证:AE=AF;
(1)证明:∵四边形ABCD是菱形,
∴OB=OD,AC⊥BD.
∵BF=DE,
∴BF-OB=DE-OD,
即OF=OE.∴AE=AF.
图S1-1-9
(2)若BE=AE,BD=2AC=16,求线段EF的长.
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC.
∵BD=2AC=16,∴OA=4,OB=8.
设BE=AE=x,则OE=OB-BE=8-x.
在Rt△AOE中,AE2=OA2+OE2,即x2=(8-x)2+42.解得x=5.∴OE=8-5=3.由(1)知OF=OE,
∴EF=2OE=6.
图S1-1-9
8. (创新变式)如图S1-1-10,已知四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
图S1-1-10
(1)求证:AM=DM;
∴BD⊥AC,AB∥CD.∵EF⊥AC,∴EF∥BD.
∴四边形EFDB是平行四边形.
∴DF=EB.∵E是AB的中点,
∴AE=EB.∴AE=DF.
∵AB∥CD,∴∠EAM=∠FDM.
(1)证明:如答图S1-1-1,连接BD.
∵四边形ABCD是菱形,
答图S1-1-1
在△AME和△DMF中,
∴△AME≌△DMF(AAS).
∴AM=DM.
答图S1-1-1
(2)若DF=3,求菱形ABCD的周长.
图S1-1-10
(2)解:由(1)知△AME≌△DMF,
∴AE=DF=3.
∵E为AB的中点,∴AB=2AE=6.
∴菱形ABCD的周长为6×4=24.
谢 谢!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
