第十一章 三角形单元检测题(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
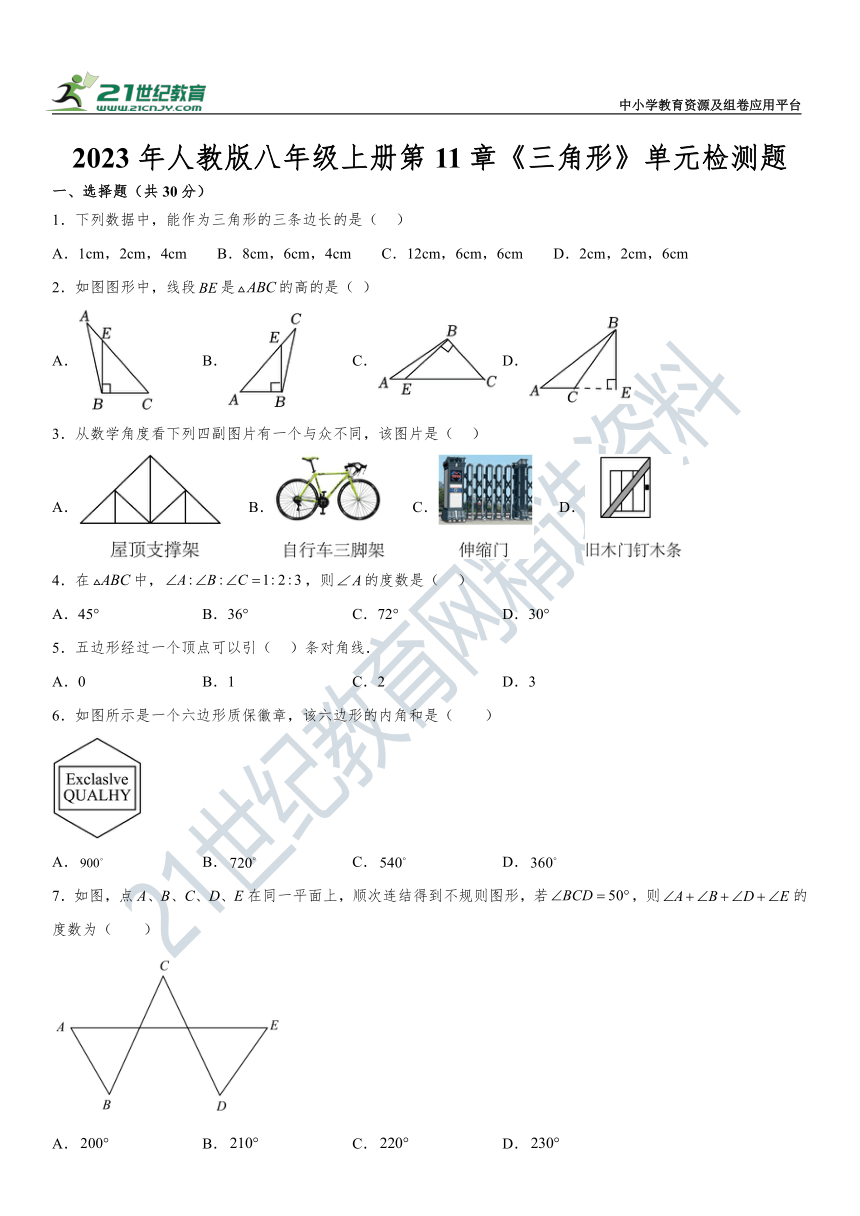
2023年人教版八年级上册第11章《三角形》单元检测题
一、选择题(共30分)
1.下列数据中,能作为三角形的三条边长的是( )
A.1cm,2cm,4cm B.8cm,6cm,4cm C.12cm,6cm,6cm D.2cm,2cm,6cm
2.如图图形中,线段是的高的是( )
A. B. C. D.
3.从数学角度看下列四副图片有一个与众不同,该图片是( )
A. B. C. D.
4.在中,,则的度数是( )
A.45° B.36° C.72° D.30°
5.五边形经过一个顶点可以引( )条对角线.
A.0 B.1 C.2 D.3
6.如图所示是一个六边形质保徽章,该六边形的内角和是( )
A. B. C. D.
7.如图,点A、B、C、D、E在同一平面上,顺次连结得到不规则图形,若,则的度数为( )
A. B. C. D.
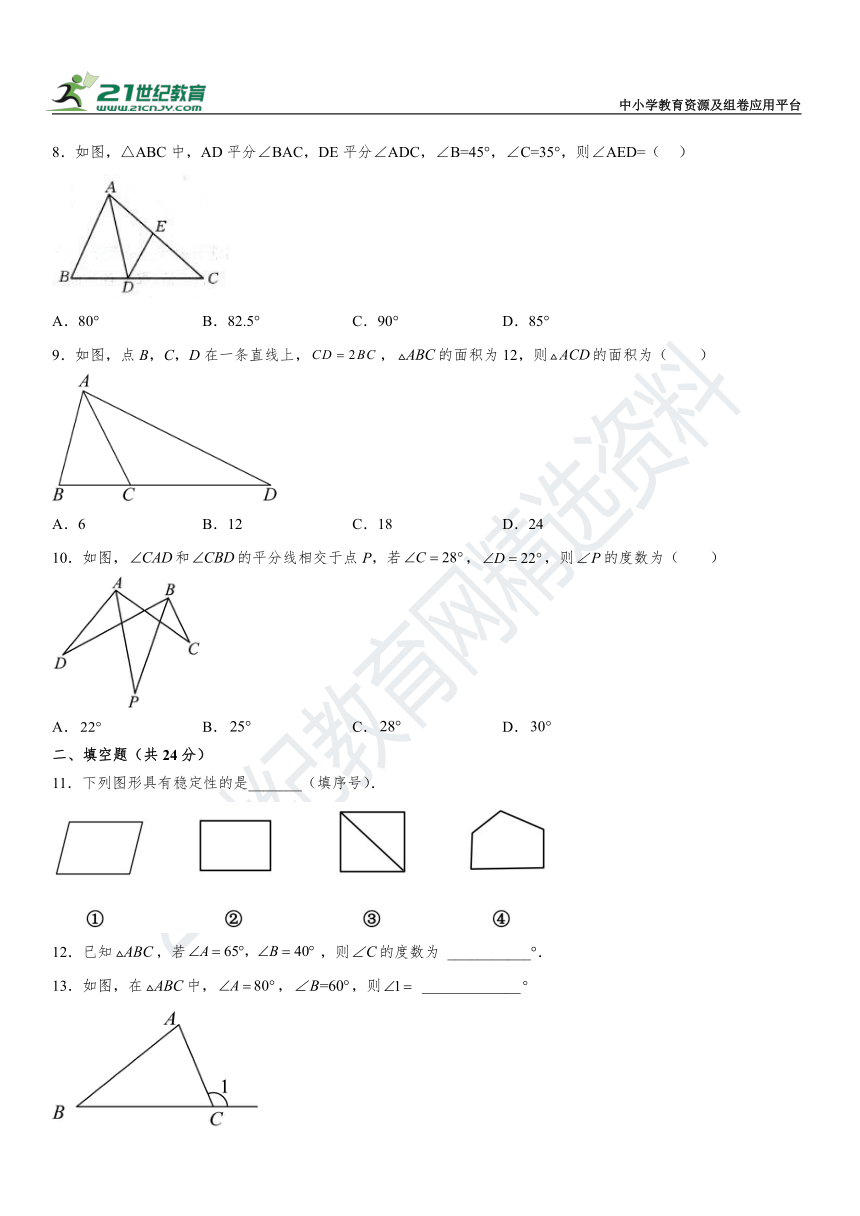
8.如图,△ABC中,AD平分∠BAC,DE平分∠ADC,∠B=45°,∠C=35°,则∠AED=( )
A.80° B.82.5° C.90° D.85°
9.如图,点B,C,D在一条直线上,,的面积为12,则的面积为( )
A.6 B.12 C.18 D.24
10.如图,和的平分线相交于点P,若,,则的度数为( )
A. B. C. D.
二、填空题(共24分)
11.下列图形具有稳定性的是_______(填序号).
12.已知,若,则的度数为 ___________°.
13.如图,在中,,,则 _____________
14.已知三角形的三边分别为3,x,4,那么x的取值范围是_______
15.若一个多边形的每个内角均为,则这个多边形的边数为___________.
16.如图,是的中线,是的中线,若,则_____.
三、解答题(共66分)
17.(6分)已知三角形的两边长分别是、,第三边为整数且为不等式组的解,求这个三角形的周长.
18.(6分)如图,已知于点,且,,求的度数.
19.(7分)如图,,分别平分,,它们交于点,求证:.
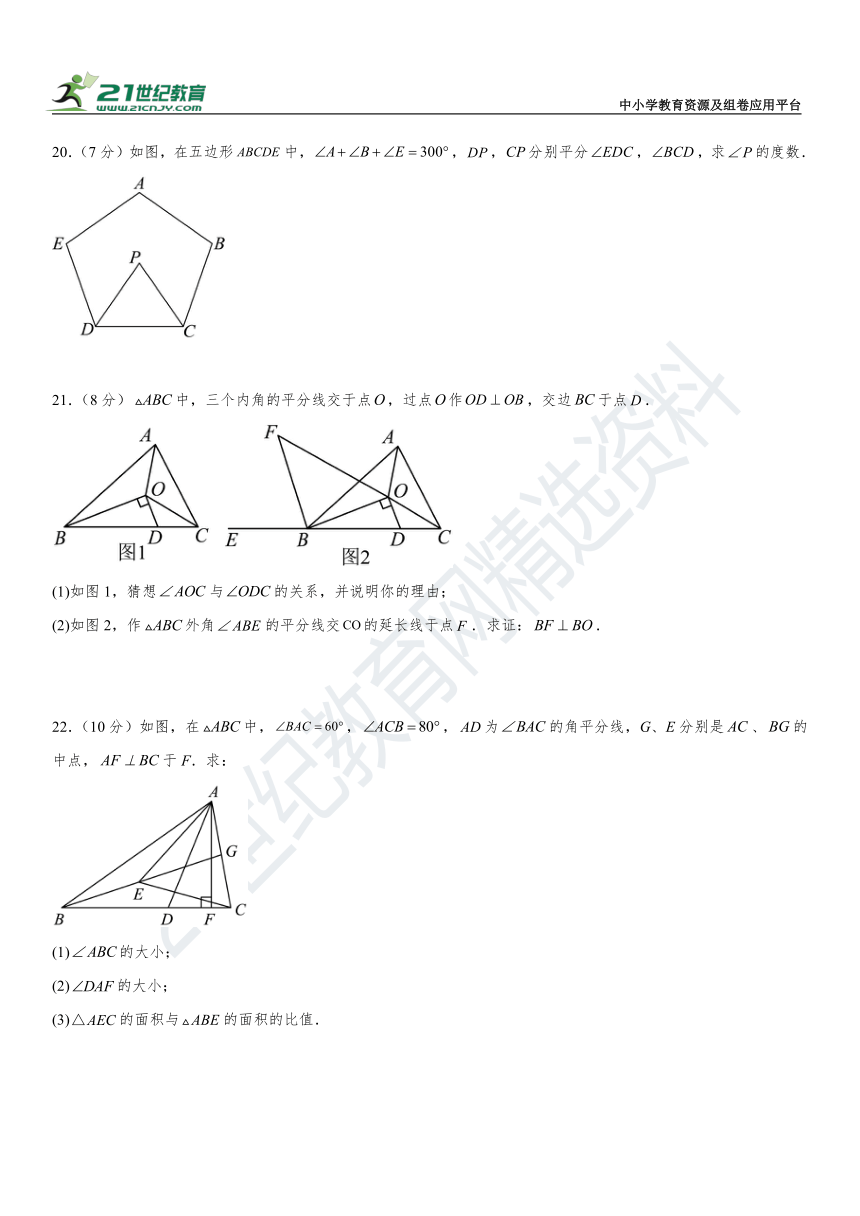
20.(7分)如图,在五边形中,,,分别平分,,求的度数.
21.(8分)中,三个内角的平分线交于点,过点作,交边于点.
(1)如图1,猜想与的关系,并说明你的理由;
(2)如图2,作外角的平分线交的延长线于点.求证:.
22.(10分)如图,在中,,,为的角平分线,G、E分别是、的中点,于F.求:
(1)的大小;
(2)的大小;
(3)的面积与的面积的比值.
23.(10分)如图1,点是内部一点,连接,并延长交于点.
(1)试探究与的大小关系;
(2)试探究与的大小关系;
(3)如图2,点,是内部两点,试探究与的大小关系.
24.(12分)根据题意解答:(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题: 如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
解:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= (∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
参考答案
1.B
【分析】根据三角形任意两边的和大于第三边逐项判断即可解答.
【详解】解:A、,不能组成三角形;
B、,能组成三角形;
C、,不能够组成三角形;
D、,不能组成三角形.
故选B.
【点睛】本题主要考查了三角形三边的条件,掌握用两条较短的线段相加,如果大于最长那条就能够组成三角形.
2.D
【分析】用三角形高的定义即可求解.
【详解】解:由三角形高的定义可知只有D选项中线段是的高,
故选D.
【点睛】本题主要考查了三角形高线的定义,熟练掌握从三角形的一个顶点向对边所在直线作垂线,顶点与垂足间的线段叫做三角形的高是解题的关键.
3.C
【分析】利用三角形的稳定性和四边形的不稳定性进行解答即可.
【详解】伸缩门是利用了四边形的不稳定性,A、B、D都是利用了三角形的稳定性.
故选:C.
【点睛】本题考查了三角形的稳定性在实际生活中的应用问题,解题的关键是分析能否在同一平面内组成三角形.
4.D
【分析】设,则,,再利用三角形内角和列方程,解方程求得的值,即可求得的度数.
【详解】设,则,,
∵,
即:,
解得:
∴,
故选:D.
【点睛】本题考查了三角形的内角和定理,一元一次方程的实际应用,设参数、利用方程的思想来解决问题是解决此类问题的关键.
5.C
【分析】根据从一个边形一个顶点出发,可以连的对角线的条数是,进行计算即可.
【详解】解∶,
∴五边形经过一个顶点可以引2条对角线.
故选∶C.
【点睛】此题主要考查了多边形的对角线,解答此类题目可以直接记忆:一个n边形一个顶点出发,可以连的对角线的条数是.
6.B
【分析】根据多边形内角和公式进行解答即可.
【详解】解:这个六边形的内角和为:,故B正确.
故选:B.
【点睛】本题主要考查了多边形内角和,解题的关键是熟练掌握多边形内角和公式.
7.D
【分析】根据得出,进而可得出,根据三角形内角和即可得出答案.
【详解】解:如图所示:
∵,
∴,
∵,,
∴,
∵,,
∴
.
故选:D.
【点睛】本题主要考查了三角形内角和以及对顶角相等等知识,解题的关键是熟练掌握三角形内角和为.
8.B
【分析】由三角形的内角和定理可得∠BAC=100°,再利用角平分线的性质得到∠EDC=47.5°,最后利用三角形外角的性质得出结果.
【详解】∵∠B=45°,∠C=35°,
∴∠BAC=180°-45°-35°=100°,
∵AD平分∠BAC,
∴∠BAD==50°,
∵∠ADC=∠B+∠BAD=50°+45°=95°, DE平分∠ADC,
∴∠EDC===47.5°,
∵∠AED=∠C+∠EDC,
∴∠AED=35°+47.5°=82.5°.
故选B.
【点睛】本题考查了三角形的内角和定理、角平分线的性质及三角形外角的性质,解题的关键是熟练掌握三角形的内角和及三角形外角的性质.
9.D
【分析】过点A作于点H,根据三角形的面积公式结合即可求出的面积.
【详解】解:过点A作于点H,
∵的面积为12,
∴,
∵,
∴的面积.
故选:D.
【点睛】本题主要考查了三角形的面积公式,掌握与有相同的高是解决问题的关键.
10.B
【分析】设,,根据角平分线的定义可知,,,再根据三角形外角的性质可得,,从而可得,再进行求解即可.
【详解】解:如图,设,,
∵平分,平分,
∴,,
∵,,
∴,
∴,即,
又∵,,
∴,
∴,即,
∴,即,
∴,
故选:B.
【点睛】本题考查角平分线的定义、三角形外角的性质,熟练掌握三角形外角的性质是解题的关键.
11.③
【分析】根据三角形具有稳定性进行求解即可.
【详解】解:∵三角形具有稳定性,四边形和五边形不具有稳定性,
∴具有稳定性的是③,
故答案为:③.
【点睛】本题考查了三角形具有稳定性,是基础题,需熟记,关键是根据三角形具有稳定性解答.
12.
【分析】根据三角形内角和定理列方程求解即可得到答案.
【详解】解:在中,,则由三角形内角和定理可得,
,
故答案为:.
【点睛】本题考查三角形内角和定理,熟记三角形三个内角和为是解决问题的关键.
13.140
【分析】利用三角形外角的性质解答即可.
【详解】解:,,
.
,
故答案为:140.
【点睛】本题考查了三角形外角的性质,解答此类题目的关键是熟记三角形内角与外角的关系.
14.1【详解】试题分析:根据三角形的任意两边之和大于第三边,两边之差小于第三边可得:
4-3<x<4+3,
即1<x<7.
故答案为1<x<7.
点睛:此题主要考查了三角形的三边关系定理,三角形中第三边的范围是:大于已知的两边的差,而小于已知两边的和.
15.9
【分析】根据多边形的内角和为,列出方程进行求解即可.
【详解】解:由题意,得:,
解得:;
故答案为:.
【点睛】本题考查多边形的内角和.熟练掌握多边形的内角和为,是解题的关键.
16.12
【分析】根据是的中线,是的中线,得到,再根据,即可得到答案.
【详解】解:∵是的中线,是的中线,
∴,
∴.
∵,
∴
故答案为:12.
【点睛】本题考查中线的性质,解题的关键是熟练掌握中线的相关知识.
17.
【分析】分别解不等式,得出整数解,根据三角形的三边关系即可求解.
【详解】解:
解不等式①得.
解不等式②得
∴
∴不等式的整数解为、、
∵
∴取
∴三角形周长为.
【点睛】本题考查了解一元一次不等式组,三角形的三边关系,正确的求得不等式的整数解是解题的关键.
18.的度数为
【分析】先根据得,再根据求出的度数,最后由,进行计算即可得到答案.
【详解】解:,
,
,
,
,
,
的度数为.
【点睛】本题主要考查了直角三角形的两个锐角互余,三角形的外角的定义,熟练掌握直角三角形的两个锐角互余,三角形的外角的定义,是解题的关键.
19.见解析
【分析】延长交于点,设,,利用三角形外角的性质求出,可得,同理求出,进而可得结论.
【详解】证明:如图,延长交于点,
设,,
∴,
,
同理可得,
,
.
【点睛】本题考查了三角形外角的性质,角的和差计算,熟知三角形的一个外角等于与它不相邻的两个内角和是解题的关键.
20.
【分析】根据五边形的内角和求出和的和,再根据角平分线及三角形内角和求出的度数.
【详解】解:五边形的内角和等于,,
;
,分别平分,,
,
;
故答案为:.
【点睛】本题主要考查了多边形的内角和公式、角平分线的定义等知识点,熟记公式以及整体思想的运用是解答本题的关键.
21.(1)
(2)见解析
【分析】(1)利用角平分线的定义和三角形的内角和定理,结合三角形的外角性质得到即可;
(2)利用角平分线的定义和平角定义求解即可.
【详解】(1)解:.理由为:
∵中,三个内角的平分线交于点,
∴,,,
∴,
∵,
∴,
∴,
∴;
(2)证明:∵平分,平分,
∴,,
∴,
∴.
【点睛】本题考查三角形的内角和定理、三角形的外角性质、角平分线的定义,熟练掌握三角形的外角性质是解答的关键.
22.(1)
(2)证明见解析
(3)
【分析】(1)根据三角形内角和定理即可求解;
(2)由角平分线的定义可得,再由垂线的定义可得,再根据三角形内角和定理求得,即可求解;
(3)由G为的中点,E为的中点,可得,,从而可得,,可得,即可求解.
【详解】(1)解:∵,
又∵,,
∴;
(2)解:∵ 为的平分线,,
,
又,
,
∴,
∴;
(3)解:∵G为的中点,
∴,
∴,
又∵E为的中点,
∴,
∴,
∴,
∴.
【点睛】本题考查角平分线的定义、垂线的定义、三角形内角和定理,熟练掌握三角形内角和定理是解题的关键.
23.(1),理由见解析
(2),理由见解析
(3),理由见解析
【分析】(1)利用三角形的两边之和大于第三边解题即可;
(2)在和中,利用三角形的两边之和大于第三边解题即可;
(3)延长交的延长线于G,交于点F,在、和中,利用三角形的两边之和大于第三边解题即可.
【详解】(1)解:,理由为:
,
∴
即:
(2),理由为:
在中,,
在中,,
两式相加得:+
即:
(3),理由为:
如图,延长交的延长线于G,交于点F,
在中,,①
在中,,②
中,,③
得:
【点睛】本题考查三角形的三边关系,熟练掌握三角形的三遍之间的关系是解题的关键.
24.(1)证明见解析;(2)①∠P=26゜;②∠P=180°﹣(∠B+∠D);③∠P=90°+ (∠B+∠D).
【分析】(1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
②根据四边形的内角和等于360°,可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解;
③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.
【详解】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜, ∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)①∠P=26゜.
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4.由(1)的结论得:∠PAD+∠P=∠PCD+∠D ①,∠PAB+∠P=∠PCB+∠B ②,∵∠PAB=∠1,∠1=∠2,∴∠PAB=∠2,∴∠2+∠P=∠3+∠B ③,①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P=(∠B+∠D )=26°.
②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,∴2∠P+∠B+∠D=360°,
∴∠P=180°﹣(∠B+∠D);
③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,∠2+∠P=(180°﹣∠3)+∠D,∴2∠P=180°+∠D+∠B,∴∠P=90°+ (∠B+∠D).
【点睛】本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.
中小学教育资源及组卷应用平台
2023年人教版八年级上册第11章《三角形》单元检测题
一、选择题(共30分)
1.下列数据中,能作为三角形的三条边长的是( )
A.1cm,2cm,4cm B.8cm,6cm,4cm C.12cm,6cm,6cm D.2cm,2cm,6cm
2.如图图形中,线段是的高的是( )
A. B. C. D.
3.从数学角度看下列四副图片有一个与众不同,该图片是( )
A. B. C. D.
4.在中,,则的度数是( )
A.45° B.36° C.72° D.30°
5.五边形经过一个顶点可以引( )条对角线.
A.0 B.1 C.2 D.3
6.如图所示是一个六边形质保徽章,该六边形的内角和是( )
A. B. C. D.
7.如图,点A、B、C、D、E在同一平面上,顺次连结得到不规则图形,若,则的度数为( )
A. B. C. D.
8.如图,△ABC中,AD平分∠BAC,DE平分∠ADC,∠B=45°,∠C=35°,则∠AED=( )
A.80° B.82.5° C.90° D.85°
9.如图,点B,C,D在一条直线上,,的面积为12,则的面积为( )
A.6 B.12 C.18 D.24
10.如图,和的平分线相交于点P,若,,则的度数为( )
A. B. C. D.
二、填空题(共24分)
11.下列图形具有稳定性的是_______(填序号).
12.已知,若,则的度数为 ___________°.
13.如图,在中,,,则 _____________
14.已知三角形的三边分别为3,x,4,那么x的取值范围是_______
15.若一个多边形的每个内角均为,则这个多边形的边数为___________.
16.如图,是的中线,是的中线,若,则_____.
三、解答题(共66分)
17.(6分)已知三角形的两边长分别是、,第三边为整数且为不等式组的解,求这个三角形的周长.
18.(6分)如图,已知于点,且,,求的度数.
19.(7分)如图,,分别平分,,它们交于点,求证:.
20.(7分)如图,在五边形中,,,分别平分,,求的度数.
21.(8分)中,三个内角的平分线交于点,过点作,交边于点.
(1)如图1,猜想与的关系,并说明你的理由;
(2)如图2,作外角的平分线交的延长线于点.求证:.
22.(10分)如图,在中,,,为的角平分线,G、E分别是、的中点,于F.求:
(1)的大小;
(2)的大小;
(3)的面积与的面积的比值.
23.(10分)如图1,点是内部一点,连接,并延长交于点.
(1)试探究与的大小关系;
(2)试探究与的大小关系;
(3)如图2,点,是内部两点,试探究与的大小关系.
24.(12分)根据题意解答:(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题: 如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
解:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得:∠P+∠3=∠1+∠B①,∠P+∠2=∠4+∠D②,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= (∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
参考答案
1.B
【分析】根据三角形任意两边的和大于第三边逐项判断即可解答.
【详解】解:A、,不能组成三角形;
B、,能组成三角形;
C、,不能够组成三角形;
D、,不能组成三角形.
故选B.
【点睛】本题主要考查了三角形三边的条件,掌握用两条较短的线段相加,如果大于最长那条就能够组成三角形.
2.D
【分析】用三角形高的定义即可求解.
【详解】解:由三角形高的定义可知只有D选项中线段是的高,
故选D.
【点睛】本题主要考查了三角形高线的定义,熟练掌握从三角形的一个顶点向对边所在直线作垂线,顶点与垂足间的线段叫做三角形的高是解题的关键.
3.C
【分析】利用三角形的稳定性和四边形的不稳定性进行解答即可.
【详解】伸缩门是利用了四边形的不稳定性,A、B、D都是利用了三角形的稳定性.
故选:C.
【点睛】本题考查了三角形的稳定性在实际生活中的应用问题,解题的关键是分析能否在同一平面内组成三角形.
4.D
【分析】设,则,,再利用三角形内角和列方程,解方程求得的值,即可求得的度数.
【详解】设,则,,
∵,
即:,
解得:
∴,
故选:D.
【点睛】本题考查了三角形的内角和定理,一元一次方程的实际应用,设参数、利用方程的思想来解决问题是解决此类问题的关键.
5.C
【分析】根据从一个边形一个顶点出发,可以连的对角线的条数是,进行计算即可.
【详解】解∶,
∴五边形经过一个顶点可以引2条对角线.
故选∶C.
【点睛】此题主要考查了多边形的对角线,解答此类题目可以直接记忆:一个n边形一个顶点出发,可以连的对角线的条数是.
6.B
【分析】根据多边形内角和公式进行解答即可.
【详解】解:这个六边形的内角和为:,故B正确.
故选:B.
【点睛】本题主要考查了多边形内角和,解题的关键是熟练掌握多边形内角和公式.
7.D
【分析】根据得出,进而可得出,根据三角形内角和即可得出答案.
【详解】解:如图所示:
∵,
∴,
∵,,
∴,
∵,,
∴
.
故选:D.
【点睛】本题主要考查了三角形内角和以及对顶角相等等知识,解题的关键是熟练掌握三角形内角和为.
8.B
【分析】由三角形的内角和定理可得∠BAC=100°,再利用角平分线的性质得到∠EDC=47.5°,最后利用三角形外角的性质得出结果.
【详解】∵∠B=45°,∠C=35°,
∴∠BAC=180°-45°-35°=100°,
∵AD平分∠BAC,
∴∠BAD==50°,
∵∠ADC=∠B+∠BAD=50°+45°=95°, DE平分∠ADC,
∴∠EDC===47.5°,
∵∠AED=∠C+∠EDC,
∴∠AED=35°+47.5°=82.5°.
故选B.
【点睛】本题考查了三角形的内角和定理、角平分线的性质及三角形外角的性质,解题的关键是熟练掌握三角形的内角和及三角形外角的性质.
9.D
【分析】过点A作于点H,根据三角形的面积公式结合即可求出的面积.
【详解】解:过点A作于点H,
∵的面积为12,
∴,
∵,
∴的面积.
故选:D.
【点睛】本题主要考查了三角形的面积公式,掌握与有相同的高是解决问题的关键.
10.B
【分析】设,,根据角平分线的定义可知,,,再根据三角形外角的性质可得,,从而可得,再进行求解即可.
【详解】解:如图,设,,
∵平分,平分,
∴,,
∵,,
∴,
∴,即,
又∵,,
∴,
∴,即,
∴,即,
∴,
故选:B.
【点睛】本题考查角平分线的定义、三角形外角的性质,熟练掌握三角形外角的性质是解题的关键.
11.③
【分析】根据三角形具有稳定性进行求解即可.
【详解】解:∵三角形具有稳定性,四边形和五边形不具有稳定性,
∴具有稳定性的是③,
故答案为:③.
【点睛】本题考查了三角形具有稳定性,是基础题,需熟记,关键是根据三角形具有稳定性解答.
12.
【分析】根据三角形内角和定理列方程求解即可得到答案.
【详解】解:在中,,则由三角形内角和定理可得,
,
故答案为:.
【点睛】本题考查三角形内角和定理,熟记三角形三个内角和为是解决问题的关键.
13.140
【分析】利用三角形外角的性质解答即可.
【详解】解:,,
.
,
故答案为:140.
【点睛】本题考查了三角形外角的性质,解答此类题目的关键是熟记三角形内角与外角的关系.
14.1
4-3<x<4+3,
即1<x<7.
故答案为1<x<7.
点睛:此题主要考查了三角形的三边关系定理,三角形中第三边的范围是:大于已知的两边的差,而小于已知两边的和.
15.9
【分析】根据多边形的内角和为,列出方程进行求解即可.
【详解】解:由题意,得:,
解得:;
故答案为:.
【点睛】本题考查多边形的内角和.熟练掌握多边形的内角和为,是解题的关键.
16.12
【分析】根据是的中线,是的中线,得到,再根据,即可得到答案.
【详解】解:∵是的中线,是的中线,
∴,
∴.
∵,
∴
故答案为:12.
【点睛】本题考查中线的性质,解题的关键是熟练掌握中线的相关知识.
17.
【分析】分别解不等式,得出整数解,根据三角形的三边关系即可求解.
【详解】解:
解不等式①得.
解不等式②得
∴
∴不等式的整数解为、、
∵
∴取
∴三角形周长为.
【点睛】本题考查了解一元一次不等式组,三角形的三边关系,正确的求得不等式的整数解是解题的关键.
18.的度数为
【分析】先根据得,再根据求出的度数,最后由,进行计算即可得到答案.
【详解】解:,
,
,
,
,
,
的度数为.
【点睛】本题主要考查了直角三角形的两个锐角互余,三角形的外角的定义,熟练掌握直角三角形的两个锐角互余,三角形的外角的定义,是解题的关键.
19.见解析
【分析】延长交于点,设,,利用三角形外角的性质求出,可得,同理求出,进而可得结论.
【详解】证明:如图,延长交于点,
设,,
∴,
,
同理可得,
,
.
【点睛】本题考查了三角形外角的性质,角的和差计算,熟知三角形的一个外角等于与它不相邻的两个内角和是解题的关键.
20.
【分析】根据五边形的内角和求出和的和,再根据角平分线及三角形内角和求出的度数.
【详解】解:五边形的内角和等于,,
;
,分别平分,,
,
;
故答案为:.
【点睛】本题主要考查了多边形的内角和公式、角平分线的定义等知识点,熟记公式以及整体思想的运用是解答本题的关键.
21.(1)
(2)见解析
【分析】(1)利用角平分线的定义和三角形的内角和定理,结合三角形的外角性质得到即可;
(2)利用角平分线的定义和平角定义求解即可.
【详解】(1)解:.理由为:
∵中,三个内角的平分线交于点,
∴,,,
∴,
∵,
∴,
∴,
∴;
(2)证明:∵平分,平分,
∴,,
∴,
∴.
【点睛】本题考查三角形的内角和定理、三角形的外角性质、角平分线的定义,熟练掌握三角形的外角性质是解答的关键.
22.(1)
(2)证明见解析
(3)
【分析】(1)根据三角形内角和定理即可求解;
(2)由角平分线的定义可得,再由垂线的定义可得,再根据三角形内角和定理求得,即可求解;
(3)由G为的中点,E为的中点,可得,,从而可得,,可得,即可求解.
【详解】(1)解:∵,
又∵,,
∴;
(2)解:∵ 为的平分线,,
,
又,
,
∴,
∴;
(3)解:∵G为的中点,
∴,
∴,
又∵E为的中点,
∴,
∴,
∴,
∴.
【点睛】本题考查角平分线的定义、垂线的定义、三角形内角和定理,熟练掌握三角形内角和定理是解题的关键.
23.(1),理由见解析
(2),理由见解析
(3),理由见解析
【分析】(1)利用三角形的两边之和大于第三边解题即可;
(2)在和中,利用三角形的两边之和大于第三边解题即可;
(3)延长交的延长线于G,交于点F,在、和中,利用三角形的两边之和大于第三边解题即可.
【详解】(1)解:,理由为:
,
∴
即:
(2),理由为:
在中,,
在中,,
两式相加得:+
即:
(3),理由为:
如图,延长交的延长线于G,交于点F,
在中,,①
在中,,②
中,,③
得:
【点睛】本题考查三角形的三边关系,熟练掌握三角形的三遍之间的关系是解题的关键.
24.(1)证明见解析;(2)①∠P=26゜;②∠P=180°﹣(∠B+∠D);③∠P=90°+ (∠B+∠D).
【分析】(1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
②根据四边形的内角和等于360°,可得(180°﹣∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°﹣∠3)+∠D=360°,然后整理即可得解;
③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.
【详解】解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜, ∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)①∠P=26゜.
∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4.由(1)的结论得:∠PAD+∠P=∠PCD+∠D ①,∠PAB+∠P=∠PCB+∠B ②,∵∠PAB=∠1,∠1=∠2,∴∠PAB=∠2,∴∠2+∠P=∠3+∠B ③,①+③得∠2+∠P+∠PAD+∠P=∠3+∠B+∠PCD+∠D,即2∠P+180°=∠B+∠D+180°,
∴∠P=(∠B+∠D )=26°.
②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴(180°﹣2∠1)+∠B=(180°﹣2∠4)+∠D,在四边形APCB中,(180°﹣∠1)+∠P+∠4+∠B=360°,在四边形APCD中,∠2+∠P+(180°﹣∠3)+∠D=360°,∴2∠P+∠B+∠D=360°,
∴∠P=180°﹣(∠B+∠D);
③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,∠2+∠P=(180°﹣∠3)+∠D,∴2∠P=180°+∠D+∠B,∴∠P=90°+ (∠B+∠D).
【点睛】本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.
