数学人教A版(2019)选择性必修第一册1.2空间向量基本定理(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.2空间向量基本定理(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-05 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
选修一《第一章 空间向量与立体几何》
1.2 空间向量基本定理
回顾:平面向量基本定理
若 , 是同一平面内的两个不共线向量,则对于这一平面内的任一向量,
有且只有一对实数x,y,使=x+y.
若, 不共线,则把{,}叫做表示这一平面内所有向量的基底.
平面内任一向量可用2个不共线的向量表示
空间中任一向量可用3个不共面的向量表示吗?
类比推广
空间中任一向量可用3个两两垂直且不共面的向量表示吗?
引入:空间向量的分解与表示
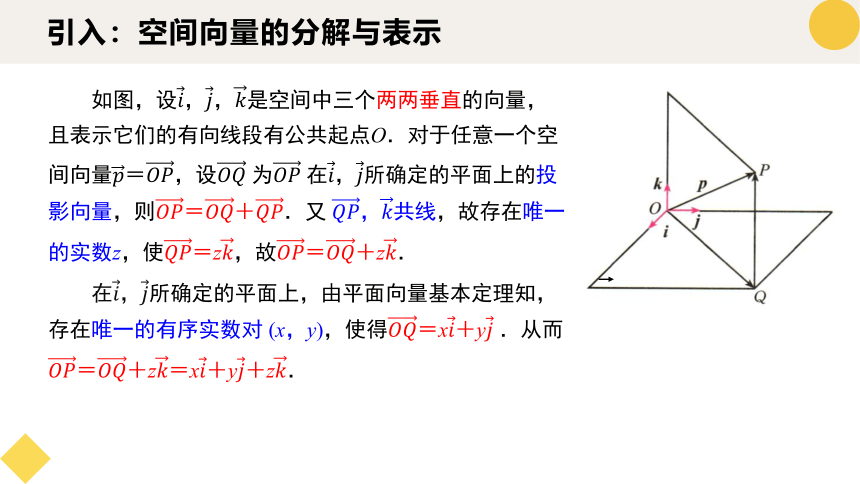
如图,设,,是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点O.对于任意一个空间向量=,设 为 在,所确定的平面上的投影向量,则=+.又 ,共线,故存在唯一的实数z,使=z,故=+z.
在,所确定的平面上,由平面向量基本定理知,存在唯一的有序实数对 (x,y),使得=x+y .从而 =+z=x+y+z.
引入:空间向量的分解与表示
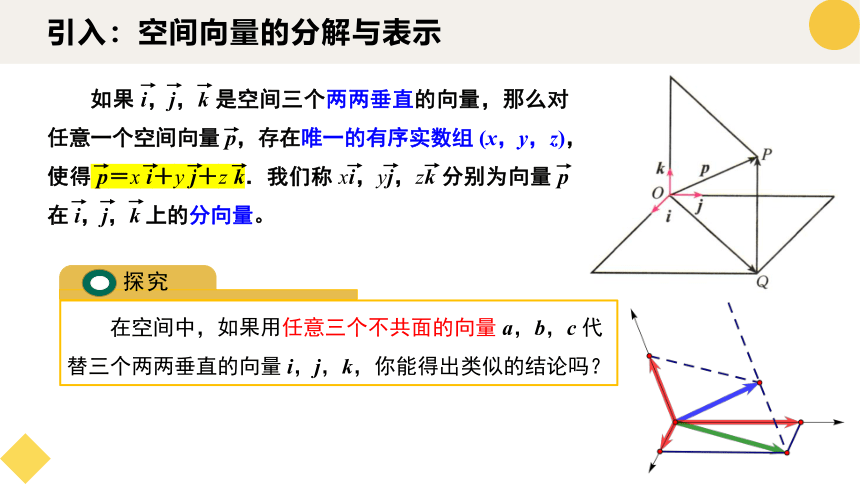
如果 i,j,k 是空间三个两两垂直的向量,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得 p=x i+y j+z k.我们称 xi,yj,zk 分别为向量 p 在 i,j,k 上的分向量。
在空间中,如果用任意三个不共面的向量 a,b,c 代替三个两两垂直的向量 i,j,k,你能得出类似的结论吗?
探究
新知1.空间向量基本定理
定理:如果三个向量 ,,不共面,那么对任意一个空间向量,
存在唯一的有序实数组 (x,y,z),使得=x+y+z.
把{,,}叫做空间的一个基底,,,叫做基向量.
①空间中任意三个不共面的向量都可以构成空间的一个基底.
②单位正交基底{}:基底中的三个基向量两两垂直,且长度都为1.
③把空间向量进行正交分解:把任意一个空间向量分解为三个两两垂直的向量, 即=x+y+z.
【基础巩固】基底的理解
P12-练习1.已知{,,}是空间的一个基底,从中选哪一个向量,一定可以与向量=构成空间的另一个基底?
P15-2.若{,,}构成空间的一个基底,则下列向量不共面的是( )
A.+,, B.,+,
C.+,, D.+,++,
若三个向量中存在一个向量可用另外两个向量表示,则三向量共面,不可构成基底.
【升级巩固】基底的判断
假设三个向量共面,建立x,y的方程组,若有解,则不可构成基底;若无解,则可构成基底.
若三个向量中存在一个向量可用另外两个向量表示,则三向量共面,不可构成基底.
小结:基底的判断
【基底法的应用1】表示空间向量
P12-例1.如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且 MN=ON,AP=AN,用向量,,表示.
同类题:P15-3、4
以三角形法则或平行四边形法则为切入点,建立目标向量与基底的关系.
【基底法的应用1】表示空间向量
P12-练习3.如图,已知平行六面体OABC-O′A′B′C′,点G是侧面BB′C′C 的中心,且=a,=b,=c .
(1){a,b,c} 是否构成空间的一个基底?
(2)如果 {a,b,c} 构成空间的一个基底,那么用它表示下列向量:
,,,.
是
【基底法的应用2】求线段长度(向量的模)
四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA=2,且PA与AB,AD的夹角均为60°,点M是PC的中点,求BM的长.
【基底法的应用3】求异面直线所成角(向量夹角)
P13-例3.如图,正方体 ABCD-A′B′C′D′ 的棱长为 1,E,F,G 分别为 C′D′,A′D′,D′D 的中点.求CE与AG所成角的余弦值.
同类:P14-2
P15-7(2)
【基底法的应用4】证线线垂直(向量数量积为0)
P13-例2.如图,在平行六面体 ABCD-A1B1C1D1 中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N 分别为 D1C1,C1B1 的中点.求证 :MN⊥AC1.
同类题:P14-3
P15-6/7(1)
课堂小结:空间向量的基底
1.基底的判断:若三个向量不共面,则可作为空间向量的一个基底.
①存在一个向量可以另外两个向量表示,则三向量共面;
②假设三向量共面,建立x,y的方程组,若无解,则不共面,若有解,则共面.
2.基底的构建:常依托正方体、长方体、平行六面体、四面体等几何体,用
从同一顶点出发的三条棱对应的向量为基底,并尽量选已知夹角和长度的向量.
3.用基底表示向量:结合向量的加减法运算法则寻找目标向量与基向量的关系.
4.基底的运用:用基底法解决立体几何中的垂直、共线、角度、模长等问题.
课堂小结:空间向量的基底
4.基底的运用:用基底法解决立体几何中的垂直、共线、角度、模长等问题.
(4)若要求线段长度,则转化为求向量的模.
新知:空间向量的投影向量
长度比+方向
综合运用——基底法
P15-7.如图,在棱长为2的正方体 ABCD-A1B1C1D1中,E,F分别是D1D与BD的中点,点G在CD上,且CG=GD.
(1)求证:EF⊥B1C; (2)求EF与C1G所成角的余弦值.
综合运用——基底法
P15-7.如图,在棱长为2的正方体 ABCD-A1B1C1D1中,E,F分别是D1D与BD的中点,点G在CD上,且CG=GD.
(1)求证:EF⊥B1C; (2)求EF与C1G所成角的余弦值.
拓广探索
①四面体中的3组对棱中有2组两两垂直,
则另一组对棱也互相垂直.
P15-8.已知四面体中三组相对棱的中点间的距离都相等,
求证:这个四面体的相对的棱两两垂直。
P10-9.如图,在四面体OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB.
②四面体中3组对棱的中点间的距离相等,
则这3组对棱两两垂直.
P10-8.(三垂线定理)若平面内的一条直线与这个平面的斜线在面内的射影垂直,则它与这个斜线也垂直.
好学数学,数学好学,学好数学。
FIGHTING
选修一《第一章 空间向量与立体几何》
1.2 空间向量基本定理
回顾:平面向量基本定理
若 , 是同一平面内的两个不共线向量,则对于这一平面内的任一向量,
有且只有一对实数x,y,使=x+y.
若, 不共线,则把{,}叫做表示这一平面内所有向量的基底.
平面内任一向量可用2个不共线的向量表示
空间中任一向量可用3个不共面的向量表示吗?
类比推广
空间中任一向量可用3个两两垂直且不共面的向量表示吗?
引入:空间向量的分解与表示
如图,设,,是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点O.对于任意一个空间向量=,设 为 在,所确定的平面上的投影向量,则=+.又 ,共线,故存在唯一的实数z,使=z,故=+z.
在,所确定的平面上,由平面向量基本定理知,存在唯一的有序实数对 (x,y),使得=x+y .从而 =+z=x+y+z.
引入:空间向量的分解与表示
如果 i,j,k 是空间三个两两垂直的向量,那么对任意一个空间向量 p,存在唯一的有序实数组 (x,y,z),使得 p=x i+y j+z k.我们称 xi,yj,zk 分别为向量 p 在 i,j,k 上的分向量。
在空间中,如果用任意三个不共面的向量 a,b,c 代替三个两两垂直的向量 i,j,k,你能得出类似的结论吗?
探究
新知1.空间向量基本定理
定理:如果三个向量 ,,不共面,那么对任意一个空间向量,
存在唯一的有序实数组 (x,y,z),使得=x+y+z.
把{,,}叫做空间的一个基底,,,叫做基向量.
①空间中任意三个不共面的向量都可以构成空间的一个基底.
②单位正交基底{}:基底中的三个基向量两两垂直,且长度都为1.
③把空间向量进行正交分解:把任意一个空间向量分解为三个两两垂直的向量, 即=x+y+z.
【基础巩固】基底的理解
P12-练习1.已知{,,}是空间的一个基底,从中选哪一个向量,一定可以与向量=构成空间的另一个基底?
P15-2.若{,,}构成空间的一个基底,则下列向量不共面的是( )
A.+,, B.,+,
C.+,, D.+,++,
若三个向量中存在一个向量可用另外两个向量表示,则三向量共面,不可构成基底.
【升级巩固】基底的判断
假设三个向量共面,建立x,y的方程组,若有解,则不可构成基底;若无解,则可构成基底.
若三个向量中存在一个向量可用另外两个向量表示,则三向量共面,不可构成基底.
小结:基底的判断
【基底法的应用1】表示空间向量
P12-例1.如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且 MN=ON,AP=AN,用向量,,表示.
同类题:P15-3、4
以三角形法则或平行四边形法则为切入点,建立目标向量与基底的关系.
【基底法的应用1】表示空间向量
P12-练习3.如图,已知平行六面体OABC-O′A′B′C′,点G是侧面BB′C′C 的中心,且=a,=b,=c .
(1){a,b,c} 是否构成空间的一个基底?
(2)如果 {a,b,c} 构成空间的一个基底,那么用它表示下列向量:
,,,.
是
【基底法的应用2】求线段长度(向量的模)
四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA=2,且PA与AB,AD的夹角均为60°,点M是PC的中点,求BM的长.
【基底法的应用3】求异面直线所成角(向量夹角)
P13-例3.如图,正方体 ABCD-A′B′C′D′ 的棱长为 1,E,F,G 分别为 C′D′,A′D′,D′D 的中点.求CE与AG所成角的余弦值.
同类:P14-2
P15-7(2)
【基底法的应用4】证线线垂直(向量数量积为0)
P13-例2.如图,在平行六面体 ABCD-A1B1C1D1 中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N 分别为 D1C1,C1B1 的中点.求证 :MN⊥AC1.
同类题:P14-3
P15-6/7(1)
课堂小结:空间向量的基底
1.基底的判断:若三个向量不共面,则可作为空间向量的一个基底.
①存在一个向量可以另外两个向量表示,则三向量共面;
②假设三向量共面,建立x,y的方程组,若无解,则不共面,若有解,则共面.
2.基底的构建:常依托正方体、长方体、平行六面体、四面体等几何体,用
从同一顶点出发的三条棱对应的向量为基底,并尽量选已知夹角和长度的向量.
3.用基底表示向量:结合向量的加减法运算法则寻找目标向量与基向量的关系.
4.基底的运用:用基底法解决立体几何中的垂直、共线、角度、模长等问题.
课堂小结:空间向量的基底
4.基底的运用:用基底法解决立体几何中的垂直、共线、角度、模长等问题.
(4)若要求线段长度,则转化为求向量的模.
新知:空间向量的投影向量
长度比+方向
综合运用——基底法
P15-7.如图,在棱长为2的正方体 ABCD-A1B1C1D1中,E,F分别是D1D与BD的中点,点G在CD上,且CG=GD.
(1)求证:EF⊥B1C; (2)求EF与C1G所成角的余弦值.
综合运用——基底法
P15-7.如图,在棱长为2的正方体 ABCD-A1B1C1D1中,E,F分别是D1D与BD的中点,点G在CD上,且CG=GD.
(1)求证:EF⊥B1C; (2)求EF与C1G所成角的余弦值.
拓广探索
①四面体中的3组对棱中有2组两两垂直,
则另一组对棱也互相垂直.
P15-8.已知四面体中三组相对棱的中点间的距离都相等,
求证:这个四面体的相对的棱两两垂直。
P10-9.如图,在四面体OABC中,OA⊥BC,OB⊥AC,求证:OC⊥AB.
②四面体中3组对棱的中点间的距离相等,
则这3组对棱两两垂直.
P10-8.(三垂线定理)若平面内的一条直线与这个平面的斜线在面内的射影垂直,则它与这个斜线也垂直.
好学数学,数学好学,学好数学。
FIGHTING
