2022-2023学年鲁教版(五四制)六年级下册数学素养提升练习(尖子生培养)(无答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)六年级下册数学素养提升练习(尖子生培养)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 415.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 23:00:09 | ||
图片预览



文档简介
六年级下册数学素养提升练习(尖子生培养)
一、单选题
1.已知,则等于( )
A. B. C. D.
2.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )
A.50°、130° B.都是10°
C.50°、130°或10°、10° D.以上都不对
3.将多项式加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A. B.±4x C. D.
4.已知,,,则a、b、c的大小关系为( )
A. B. C. D.
5.下列计算结果正确的是( )
A.
B.
C.
D.
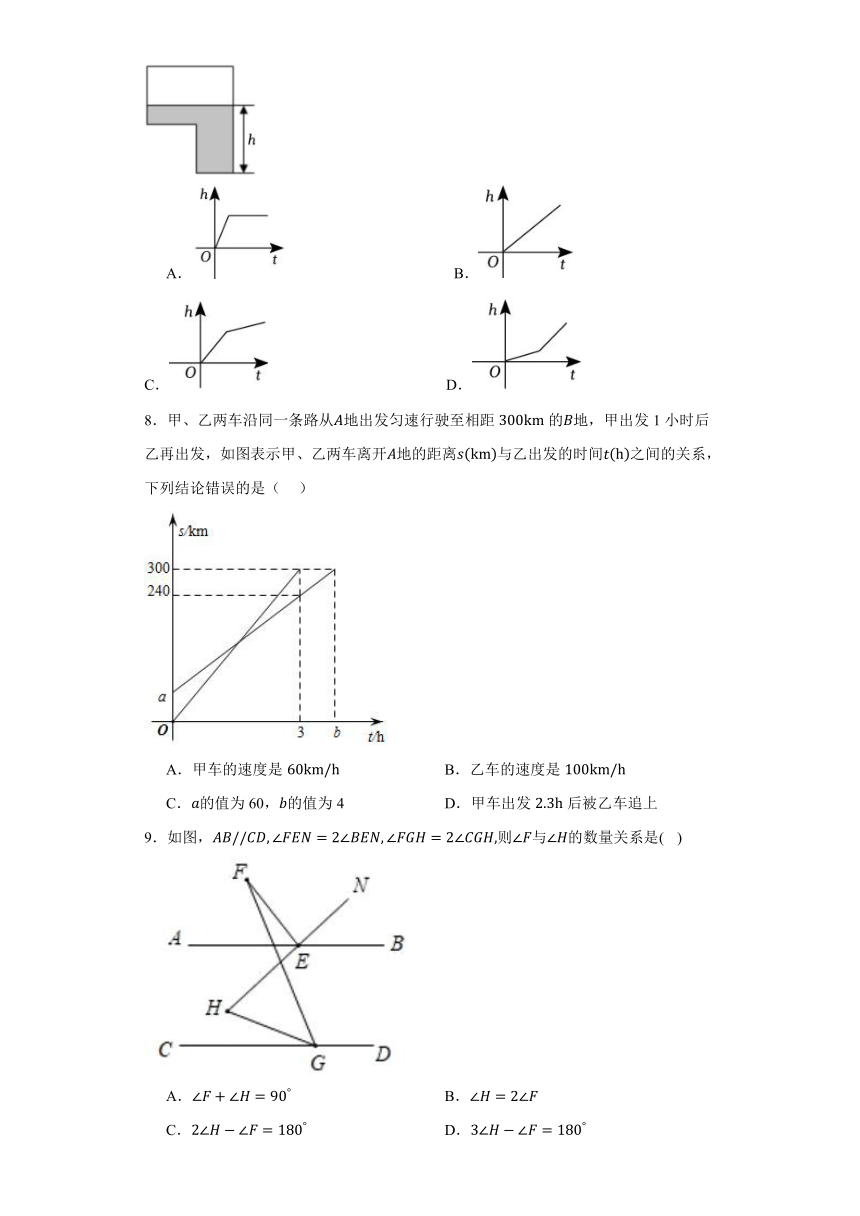
6.向高为10厘米的容器中注水,注满为止,若注水量()与水深(cm)之间的关系的图象大致如图所示,则这个容器是下列四个图中的( )
A. B. C. D.
7.如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
B.
C. D.
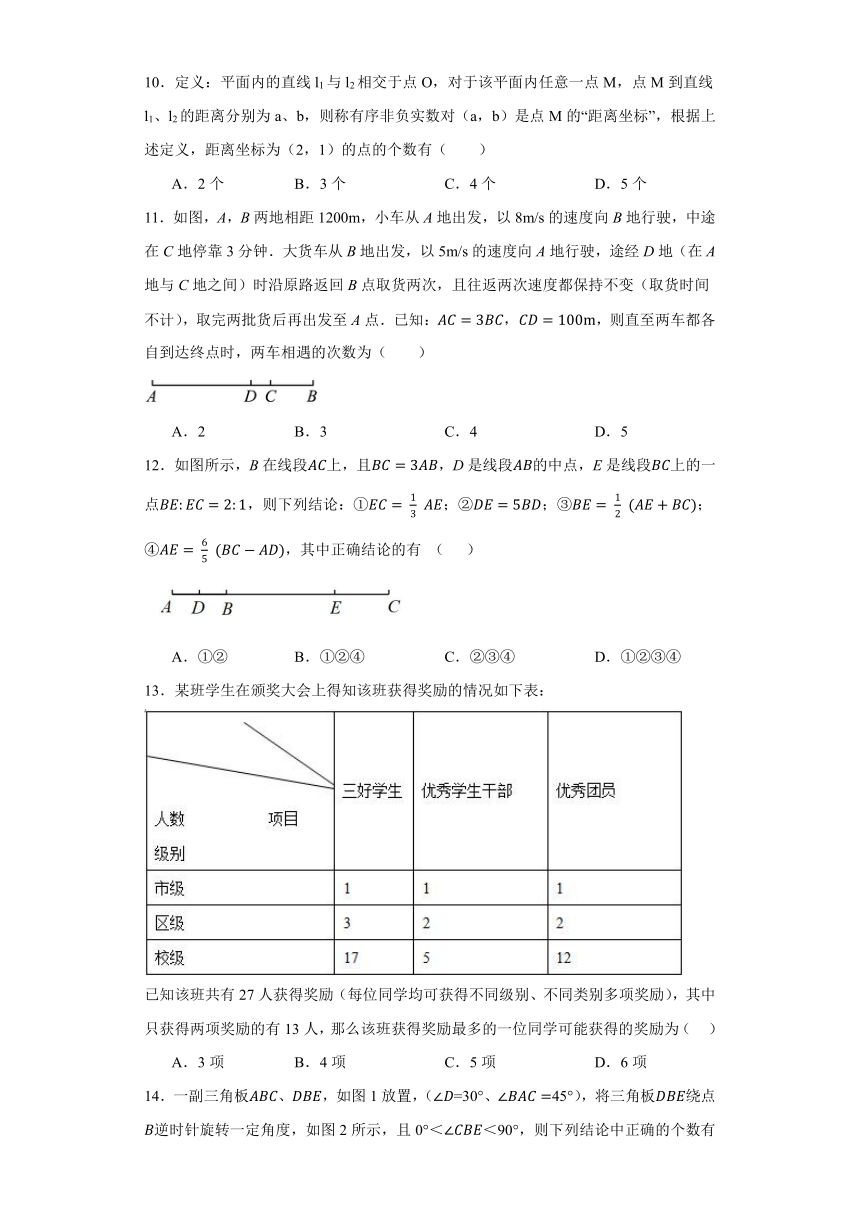
8.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
9.如图,则与的数量关系是( )
A. B.
C. D.
10.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A.2个 B.3个 C.4个 D.5个
11.如图,A,B两地相距1200m,小车从A地出发,以8m/s的速度向B地行驶,中途在C地停靠3分钟.大货车从B地出发,以5m/s的速度向A地行驶,途经D地(在A地与C地之间)时沿原路返回B点取货两次,且往返两次速度都保持不变(取货时间不计),取完两批货后再出发至A点.已知:,则直至两车都各自到达终点时,两车相遇的次数为( )
A.2 B.3 C.4 D.5
12.如图所示,B在线段上,且,D是线段的中点,E是线段上的一点,则下列结论:① ;②;③ ;④ ,其中正确结论的有 ( )
A.①② B.①②④ C.②③④ D.①②③④
13.某班学生在颁奖大会上得知该班获得奖励的情况如下表:
已知该班共有27人获得奖励(每位同学均可获得不同级别、不同类别多项奖励),其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A.3项 B.4项 C.5项 D.6项
14.一副三角板、,如图1放置,(=30°、45°),将三角板绕点逆时针旋转一定角度,如图2所示,且0°<<90°,则下列结论中正确的个数有( )
①的角度恒为105°;
②在旋转过程中,若平分,平分,的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成90°的次数为2次;
④在图1的情况下,作,则平分
A.1个 B.2个 C.3个 D.4个
15.如图,点M在线段AN的延长线上,且线段,第一次操作:分别取线段和的中点、;第二次操作:分别取线段和的中点,;第三次操作:分别取线段和的中点,;…连续这样操作2023次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
16.杨辉三角是中国古代数学杰出研究成果之一,它把(其中n为自然数)的展开式中的各项的系数直观地体现了出来,其中的展开式中的各项系数依次对应杨辉三角的第行的每一项,如下所示:
的展开式
…
根据上述材料,则的展开式中含项的系数为 ( )
A.10 B. C.40 D.
二、填空题
17.若是关于的完全平方式,则___________.
18.已知直线与直线相交于点O,,于点O,则___________.
19.设m =(2+1)(22+1)(24+1)…(264+1),则m的个位数字是_____.
20.如图,两直线AB、CD平行,则__________.
21.如图,在的内部,平分.若,,则____°(用含m、n的代数式表示).
22.如图,点A、B、C在同一条直线上,点D为的中点,点P为延长线上一动点,点E为的中点,则的值是___________.
23.为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度匀速往返跑步,已知小明的速度大于小强的速度. 在跑步的过程中,小明和小强两人之间的距离y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家____米.
24.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,其中第1个图案中有6个正三角形,第2个图案中有10个正三角形,第3个图案中有14个正三角形,…依此规律,第n个图案中有________个正三角形.(用含n的代数式表示)
三、解答题
25.如图已知线段、,
(1)线段在线段上(点C、A在点B的左侧,点D在点C的右侧)
①若线段,,M、N分别为、的中点,求的长.
②M、N分别为、的中点,求证:
(2)线段在线段的延长线上,M、N分别为、的中点,②中的结论是否成立?请画出图形,直接写出结论
26.如图,是的角分线,为的角分线.
(1)若,,求的度数;
(2)若与互为补角,求的度数;
(3)在(2)的条件下,过点O引一条射线OG,使,且,平分,求的度数?
27.如图,AD∥BC,若∠ADP=∠α,∠BCP=∠β,射线OM上有一动点P.
(1)当点P在A,B两点之间运动时,∠CPD与∠α、∠β之间有何数量关系?请说明理由
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的何数量关系.
28.数形结合是一种非常重要的数学思想,它包含两个方面,第一种是“以数解形”,第二种是“以形助数”,我国著名数学家华罗庚曾说过:“数无形时少直觉,形少数时难入微”.请你使用数形结合这种思想解决下面问题:
图1是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分为四块完成相同的小长方形,然后按照图2的形状拼成一个正方形.
(1)观察图2,用两种方法计算阴影部分的面积,可以得到一个等式,请使用代数式,,ab写出这个等式_____________.
(2)运用你所得到的公式,计算:若m、n为实数,且,,试求的值.
(3)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设,两正方形的面积和,求图中阴影部分的面积.
29.阅读:在计算的过程中,我们可以先从简单的、特殊的情形入手,再到复杂的、一般的问题,通过观察、归纳、总结,形成解决一类问题的一般方法,数学中把这样的过程叫做特殊到一般.如下所示:
【观察】①;
②;
③;
……
(1)【归纳】由此可得: ________;
(2)【应用】请运用上面的结论,解决下列问题:计算:_______;
(3)计算:______;
(4)若,求的值.
30.九年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为分)进行了一次初步统计.看到分以上(含分)有人,但没有满分,也没有低于分的.为更清楚了解本班考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示,请根据图中提供的信息解答下列问题:
(1)班级共有 名学生参加了考试,填上两个图中的空缺部分;
(2)参加考试的学生中分到分的学生有 人;
(3)若全校九年级共有名学生,则九年级成绩在分的约有名学生.
31.“互联网+”的出现,在一定程度上推动了现代物流业尤其是快递业的发展.小刚打算网购一些物品,并了解到两家快递公司的收费方式.甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价;乙公司:按物品重量每千克6元计价外再加包装费10元.设小刚网购物品的重量为x千克(x正数),根据题意列表:
物品重量(千克) 0.5 1 1.5 2 … x
甲公司费用(y甲元) 20 20 22 a … y甲
乙公司费用(y乙元) 13 16 19 22 … y乙
(1)在变化过程中的两个变量物品重量x(千克)和甲公司费用y甲(元),其中,自变量是______,因变量是______,表格中a的值为______;
(2)请直接写出表示y乙与x之间关系的表达式:__________;
(3)如图,是小刚画出的表示甲公司费用y甲(元)和乙公司费用y乙(元)分别与物品重量x(千克)关系的图象.
①图中两图象的交点A表示的意义是:______;
②若小刚网购物品的重量为4千克,如果想节省快递费用,结合图象,你认为小刚应选择的快递公司是______.
32.猜想说理:
(1)如图,,分别就图1、图2、图3写出,,的关系,并任选其中一个图形说明理由:
拓展应用:
(2)如图4,若,则 度;
(3)在图5中,若,请你用含n的代数式表示的度数.
一、单选题
1.已知,则等于( )
A. B. C. D.
2.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )
A.50°、130° B.都是10°
C.50°、130°或10°、10° D.以上都不对
3.将多项式加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( )
A. B.±4x C. D.
4.已知,,,则a、b、c的大小关系为( )
A. B. C. D.
5.下列计算结果正确的是( )
A.
B.
C.
D.
6.向高为10厘米的容器中注水,注满为止,若注水量()与水深(cm)之间的关系的图象大致如图所示,则这个容器是下列四个图中的( )
A. B. C. D.
7.如图,某蓄水池的横断面示意图,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系( )
B.
C. D.
8.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
9.如图,则与的数量关系是( )
A. B.
C. D.
10.定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )
A.2个 B.3个 C.4个 D.5个
11.如图,A,B两地相距1200m,小车从A地出发,以8m/s的速度向B地行驶,中途在C地停靠3分钟.大货车从B地出发,以5m/s的速度向A地行驶,途经D地(在A地与C地之间)时沿原路返回B点取货两次,且往返两次速度都保持不变(取货时间不计),取完两批货后再出发至A点.已知:,则直至两车都各自到达终点时,两车相遇的次数为( )
A.2 B.3 C.4 D.5
12.如图所示,B在线段上,且,D是线段的中点,E是线段上的一点,则下列结论:① ;②;③ ;④ ,其中正确结论的有 ( )
A.①② B.①②④ C.②③④ D.①②③④
13.某班学生在颁奖大会上得知该班获得奖励的情况如下表:
已知该班共有27人获得奖励(每位同学均可获得不同级别、不同类别多项奖励),其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A.3项 B.4项 C.5项 D.6项
14.一副三角板、,如图1放置,(=30°、45°),将三角板绕点逆时针旋转一定角度,如图2所示,且0°<<90°,则下列结论中正确的个数有( )
①的角度恒为105°;
②在旋转过程中,若平分,平分,的角度恒为定值;
③在旋转过程中,两块三角板的边所在直线夹角成90°的次数为2次;
④在图1的情况下,作,则平分
A.1个 B.2个 C.3个 D.4个
15.如图,点M在线段AN的延长线上,且线段,第一次操作:分别取线段和的中点、;第二次操作:分别取线段和的中点,;第三次操作:分别取线段和的中点,;…连续这样操作2023次,则每次的两个中点所形成的所有线段之和( )
A. B. C. D.
16.杨辉三角是中国古代数学杰出研究成果之一,它把(其中n为自然数)的展开式中的各项的系数直观地体现了出来,其中的展开式中的各项系数依次对应杨辉三角的第行的每一项,如下所示:
的展开式
…
根据上述材料,则的展开式中含项的系数为 ( )
A.10 B. C.40 D.
二、填空题
17.若是关于的完全平方式,则___________.
18.已知直线与直线相交于点O,,于点O,则___________.
19.设m =(2+1)(22+1)(24+1)…(264+1),则m的个位数字是_____.
20.如图,两直线AB、CD平行,则__________.
21.如图,在的内部,平分.若,,则____°(用含m、n的代数式表示).
22.如图,点A、B、C在同一条直线上,点D为的中点,点P为延长线上一动点,点E为的中点,则的值是___________.
23.为了锻炼身体,强健体魄,小明和小强约定每天在两家之间往返长跑20分钟. 两家正好在同一直线道路边上,某天小明和小强从各自的家门口同时出发,沿两家之间的直线道路按各自的速度匀速往返跑步,已知小明的速度大于小强的速度. 在跑步的过程中,小明和小强两人之间的距离y(米)与他们出发的时间x(分钟)之间的关系如图所示,在他们3次相遇中,离小明家最近那次相遇时距小明家____米.
24.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,其中第1个图案中有6个正三角形,第2个图案中有10个正三角形,第3个图案中有14个正三角形,…依此规律,第n个图案中有________个正三角形.(用含n的代数式表示)
三、解答题
25.如图已知线段、,
(1)线段在线段上(点C、A在点B的左侧,点D在点C的右侧)
①若线段,,M、N分别为、的中点,求的长.
②M、N分别为、的中点,求证:
(2)线段在线段的延长线上,M、N分别为、的中点,②中的结论是否成立?请画出图形,直接写出结论
26.如图,是的角分线,为的角分线.
(1)若,,求的度数;
(2)若与互为补角,求的度数;
(3)在(2)的条件下,过点O引一条射线OG,使,且,平分,求的度数?
27.如图,AD∥BC,若∠ADP=∠α,∠BCP=∠β,射线OM上有一动点P.
(1)当点P在A,B两点之间运动时,∠CPD与∠α、∠β之间有何数量关系?请说明理由
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的何数量关系.
28.数形结合是一种非常重要的数学思想,它包含两个方面,第一种是“以数解形”,第二种是“以形助数”,我国著名数学家华罗庚曾说过:“数无形时少直觉,形少数时难入微”.请你使用数形结合这种思想解决下面问题:
图1是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分为四块完成相同的小长方形,然后按照图2的形状拼成一个正方形.
(1)观察图2,用两种方法计算阴影部分的面积,可以得到一个等式,请使用代数式,,ab写出这个等式_____________.
(2)运用你所得到的公式,计算:若m、n为实数,且,,试求的值.
(3)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设,两正方形的面积和,求图中阴影部分的面积.
29.阅读:在计算的过程中,我们可以先从简单的、特殊的情形入手,再到复杂的、一般的问题,通过观察、归纳、总结,形成解决一类问题的一般方法,数学中把这样的过程叫做特殊到一般.如下所示:
【观察】①;
②;
③;
……
(1)【归纳】由此可得: ________;
(2)【应用】请运用上面的结论,解决下列问题:计算:_______;
(3)计算:______;
(4)若,求的值.
30.九年级一班的两位学生对本班的一次数学成绩(分数取整数,满分为分)进行了一次初步统计.看到分以上(含分)有人,但没有满分,也没有低于分的.为更清楚了解本班考试情况,他们分别用两种方式进行了统计分析,如图1和图2所示,请根据图中提供的信息解答下列问题:
(1)班级共有 名学生参加了考试,填上两个图中的空缺部分;
(2)参加考试的学生中分到分的学生有 人;
(3)若全校九年级共有名学生,则九年级成绩在分的约有名学生.
31.“互联网+”的出现,在一定程度上推动了现代物流业尤其是快递业的发展.小刚打算网购一些物品,并了解到两家快递公司的收费方式.甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价;乙公司:按物品重量每千克6元计价外再加包装费10元.设小刚网购物品的重量为x千克(x正数),根据题意列表:
物品重量(千克) 0.5 1 1.5 2 … x
甲公司费用(y甲元) 20 20 22 a … y甲
乙公司费用(y乙元) 13 16 19 22 … y乙
(1)在变化过程中的两个变量物品重量x(千克)和甲公司费用y甲(元),其中,自变量是______,因变量是______,表格中a的值为______;
(2)请直接写出表示y乙与x之间关系的表达式:__________;
(3)如图,是小刚画出的表示甲公司费用y甲(元)和乙公司费用y乙(元)分别与物品重量x(千克)关系的图象.
①图中两图象的交点A表示的意义是:______;
②若小刚网购物品的重量为4千克,如果想节省快递费用,结合图象,你认为小刚应选择的快递公司是______.
32.猜想说理:
(1)如图,,分别就图1、图2、图3写出,,的关系,并任选其中一个图形说明理由:
拓展应用:
(2)如图4,若,则 度;
(3)在图5中,若,请你用含n的代数式表示的度数.
同课章节目录
