北师大版九年级数学上册1.1 菱形的性质与判定 考点总结复习 (无答案)
文档属性
| 名称 | 北师大版九年级数学上册1.1 菱形的性质与判定 考点总结复习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 349.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 09:48:13 | ||
图片预览




文档简介
专题1.1 《菱形的性质与判定》—考点总结精练
知识点小结:
一、菱形的性质
1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.
2.菱形的性质:①菱形具有平行四边形的所有性质;
②菱形的四条边相等;
③菱形的对角线互相垂直,且菱形的每一条对角线平分它的一组对角;
④菱形既是轴对称图形,也是中心对称图形,对称轴有两条,分别是两条对角线所在的直线,对称中心是两条对角线的交点.
3.菱形的面积:①同平行四边形的面积(底×高);②对角线乘积的一半.(常用等面积法求菱形的高)
二、菱形的判定
1.菱形的判定定理:①一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四边相等的四边形是菱形.
考点总结
【考点1 利用菱形的性质和判定求角度】
【例1】(2022·驻马店期中)如图,在菱形ABCD中,∠ABC=76°,BA=BE,则∠BEA的度数为( )
A.68° B.70° C.71° D.75°
【变式1-1】(2022·绍兴中考)在菱形ABCD中,∠DAB=40°,连接AC,以点A为圆心,AC长为半径作弧,交直线AD于点E,连接CE,则∠AEC的度数是 .
【变式1-2】(2023·廊坊三模)如图,已知在菱形ABCD中,连接对角线AC,作BC边的垂直平分线EF,分别交BC、AC、AD于点F、Q、E,若∠EQD=21°,则∠CAB的度数是( )
A.33° B.37° C.42° D.49°
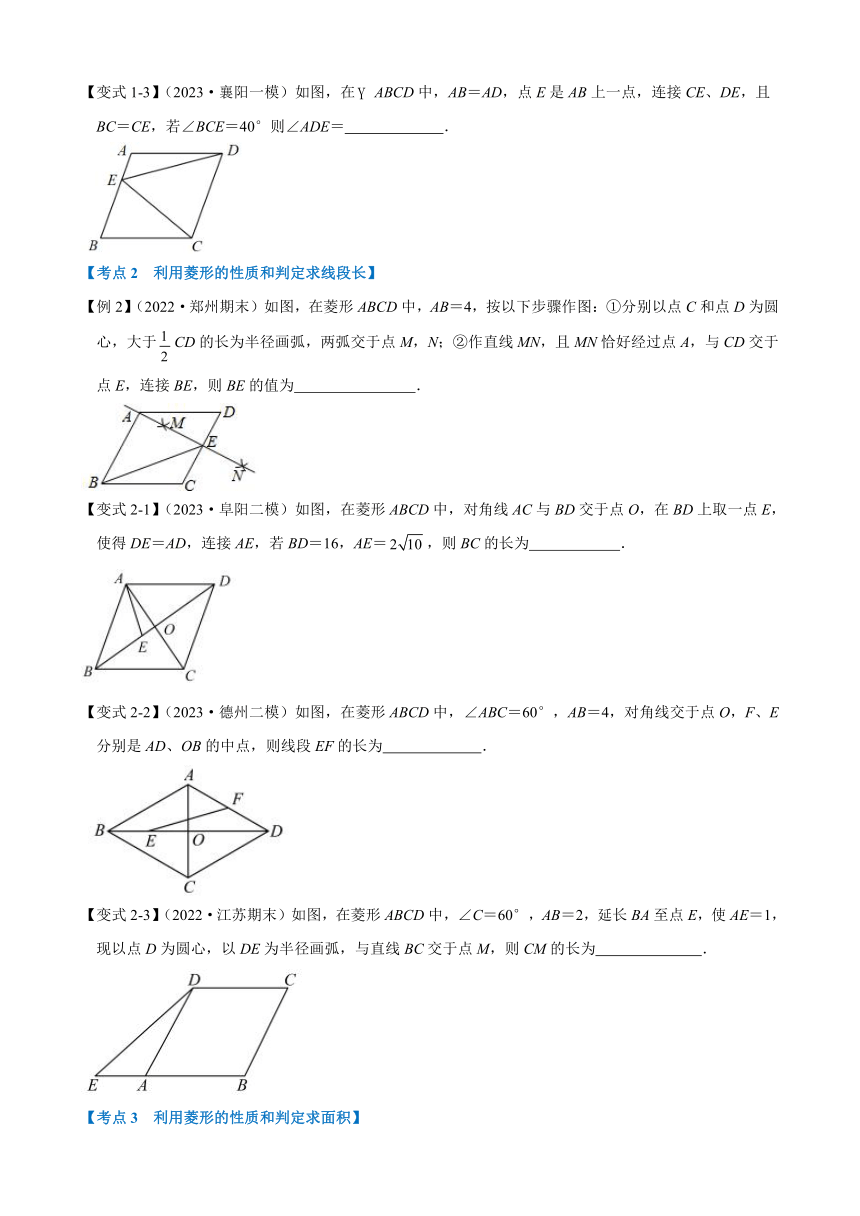
【变式1-3】(2023·襄阳一模)如图,在ABCD中,AB=AD,点E是AB上一点,连接CE、DE,且BC=CE,若∠BCE=40°则∠ADE= .
【考点2 利用菱形的性质和判定求线段长】
【例2】(2022·郑州期末)如图,在菱形ABCD中,AB=4,按以下步骤作图:①分别以点C和点D为圆心,大于CD的长为半径画弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则BE的值为 .
【变式2-1】(2023·阜阳二模)如图,在菱形ABCD中,对角线AC与BD交于点O,在BD上取一点E,使得DE=AD,连接AE,若BD=16,AE=,则BC的长为 .
【变式2-2】(2023·德州二模)如图,在菱形ABCD中,∠ABC=60°,AB=4,对角线交于点O,F、E分别是AD、OB的中点,则线段EF的长为 .
【变式2-3】(2022·江苏期末)如图,在菱形ABCD中,∠C=60°,AB=2,延长BA至点E,使AE=1,现以点D为圆心,以DE为半径画弧,与直线BC交于点M,则CM的长为 .
【考点3 利用菱形的性质和判定求面积】
【例3】(2022·长宁期末)如图,菱形ABCD的边长为2,∠DAB=60°,连接AC,将菱形ABCD绕点A旋转,使点D的对应点E落在对角线AC上,连接DE,则△DEC的面积是 .
【变式3-1】(2023·聊城中考)如图,在ABCD中,BC的垂直平分线EO交AD于点E,交BC于点O,连接BE,CE,过点C作CF∥BE,交EO的延长线于点F,连接BF.若AD=8,CE=5,则四边形BFCE的面积为 .
【变式3-2】(2022·长沙期中)如图,直线AB与x轴、y轴分别交于A、B两点,点C是OB的中点,D是AB上一点,四边形OEDC是菱形,其中B点坐标为(0,4),∠OAB=30°,则△OAE的面积为 .
【变式3-3】(2022·大庆期末)如图,在菱形ABCD中,∠BAD:∠B=1:3,DE⊥BC于点E,交对角线AC于点P,过点P作PF⊥CD于点F.若△PDF的周长为4,则菱形ABCD的面积为 .
【考点4 利用菱形的性质求点的坐标】
【例4】(2022·烟台期末)如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为 .
【变式4-1】(2023·周口三模)如图,在菱形ABCD中,AB∥y轴,且B(-1,-2),C(3,1),则点D的坐标为 .
【变式4-2】(2023·南京一模)如图,在平面直角坐标系中,菱形OABC的顶点A在y轴上,M、N分别是边OA、OC的中点,若点M,N的纵坐标分别是3,2,则点B的坐标是 .
【变式4-3】(2023·东营中考)如图,在平面直角坐标系中,菱形OABC的边长为,点B在x轴的正半轴上,且∠AOC=60°,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA’B’C’(点A’与点C重合),则点B’的坐标是 .
【考点5 菱形与折叠】
【例5】(2023·江苏)如图,在菱形ABCD中,∠A=100°,E是边AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F处,连接CF,则∠BFC的度数为( )
A.60° B.70° C.75° D.80°
【变式5-1】(2023·德阳)如图,在菱形纸片ABCD中,∠A=60°,P为AB中点,折叠该纸片使点C落在C’处,且点P在DC’上,折痕为DE,则∠CED的大小为( )
A.55° B.60° C.70° D.75°
【变式5-2】(2022·苏州)如图,菱形纸片ABCD,AB=8,∠B=60°,将该菱形纸片折叠,使点B恰好落在CD边的中点B’处,折痕与边BC、BA分别交于点M、N,则CM的长为 .
【变式5-3】(2020·红桥三模)如图,在边长为4的菱形ABCD中,∠A=60°,点M为AD的中点,连接MC,将菱形ABCD翻折,使点A的对应点E落在MC上,折痕交AB于点N,则线段CE的长度为 .
【考点6 菱形与将军饮马问题(最值)】
【例6】(2021·茂名期中)已知菱形ABCD的两条对角线长分别为10和24,M、N分别是边BC、CD的中点,点P是对角线BD上一动点,则PM+PN的最小值是 .
【变式6-1】(2022·海口)如图,菱形ABCD的面积为,AB=4,点M是AB的中点,点P是对角线AC上的一个动点,则△PBM周长的最小值为 .
【变式6-2】(2023·南阳三模)菱形OABC在平面直角坐标系中的位置如图所示,已知顶点A(8,0),点D是OA的中点,点P是对角线OB上的一个动点,∠AOC=60°,当PA+PD最短时,点P的坐标为 .
【变式6-3】(2022·九年级练习)如图,在菱形ABCD中,AB=5,对角线BD=8.点P、点Q分别是AB、BD上动点,则AQ+PQ的最小值为 .
【考点7 菱形的判定(条件选择)】
【例7】(2020·自贡三模)如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
A.BE⊥CE B.BF∥CE C.BE=CF D.AB=AC
【变式7-1】(2022·蚌埠校考)如图,四边形ABCD的对角线AC与BD相交于点O,OA=OC,OB=OD,添加下列条件仍不能判断四边形ABCD是菱形的是( )
A.BD平分∠ABC B.AC=BD C.AC⊥BD D.AB2=OA2+OB2
【变式7-2】(2023·襄阳模拟)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是( )
A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC
【变式7-3】(2023·宝鸡二模)如图,在四边形ABCD中,AB=CD,过A作AE⊥BD交BD于点E,过C作CF⊥BD交BD于点F,且AE=CF.请你在不添加辅助线的情况下,添加一个条件 ,使得四边形ABCD是菱形.
【考点8 菱形的性质与判定综合】
【例8】(2022·长治)如图,AE∥BF,∠BAD的平分线交BF于点C,∠ABC的平分线交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,过点D作DH⊥BF于点H,求DH的长.
【变式8-1】(2022·南昌期中)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若AC=4,∠BCF=120°,求菱形BCFE的面积.
【变式8-2】(2021·许昌期中)如图,E和F分别是菱形ABCD的边AB和AD的中点,且AB=15,AC=18,
(1)判断△OEF的形状,并说明理由;
(2)求四边形AEOF的面积.
【变式8-3】(2022·南阳校考)如图,△ABC中,O为AC边的中点,E为OB上一点,过点A作AD∥CE交BO延长线于点D,连接AE、CD.
(1)求证:四边形AECD是平行四边形;
(2)当△ABC满足什么条件时,四边形AECD是菱形?并说明理由;
(3)在(2)的条件下,若CD=5,AC=8,则四边形AECD的面积为 .
【考点9 菱形与中点四边形】
【例9】(2021·临沂期末)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.下列四边形的中点四边形是菱形的是( )
A.任意四边形 B.等腰梯形 C.平行四边形 D.对角线互相垂直的四边形
【变式9-1】(2022·珠海期中)如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )
A.AB∥CD B.AD=BC C.AC⊥BD D.AC=BD
【变式9-2】(2022·静海期中)如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,请你添加一个条件 ,使得四边形EFGH是菱形.
【变式9-3】(2022·泰州校考)如图,四边形ABCD中,AB与CD不平行,E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足 时,有EF⊥GH.
【考点10 菱形中的多结论问题】
【例10】(2022·哈尔滨期中)如图,菱形ABCD中,∠A=60°,E、F分别为边AB、AD的中点,DE与BF相交于点G,连接CG,以下结论:①∠BGD=120°;②S△ADE:S△GBC=2:3;③BG+DG=CG;④S菱形ABCD=AB2.其中正确的结论有( )个
A.1 B.2 C.3 D.4
【变式10-1】(2022·泰安期末)如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上一点,且DE=CD,连接BE,分别交AC、AD于点F、G,连接OG.则下列结论:①OG=AB;②由点A、B、D、E构成的四边形是菱形;③S四边形ODGF=S△ABF;④S△ACD=4S△BOG.其中正确结论的个数有( )个
A.1 B.2 C.3 D.4
【变式10-2】(2022·滨州期中)如图,ABCD的对角线AC,BD相交于点O,点E为BC边的中点,连接EO并延长交AD于点F,∠ABC=60°,BC=2AB.下列结论:①SABCD=AB·AC;②AD=4EO;③EF⊥AC;④S△BOE=S△ABC.其中正确结论的个数有( )个
A.1 B.2 C.3 D.4
【变式10-3】(2022·孝感期中)如图,在菱形ABCD中,连接AC,AB=AC,点E、F分别是AB、BC上的点,且AE=BF,连接AF、CE交于点H,连接DH交AC于点O.则下列结论:①AF=CE;②∠CHF=60°;③△ACE≌△BAF;④若AB=1,则S菱形ABCD=.其中正确的个数是( )
A.1 B.2 C.3 D.4
【考点11 菱形中的动点问题】
【例11(2022·龙岩)如图1,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则图2中的a等于( )
A.12 B.20 C.24 D.25
【变式11-1】(2023·齐齐哈尔三模)如图①,点F从菱形ABCD的顶点A出发,沿A→B→D以1cm/s的速度匀速运动到点D,图②是点F运动时△FCD的面积y(cm2)随时间x(s)的关系图象,则a的值为 .
【变式11-2】(2023·苏州一模)如图1,点P从菱形ABCD的顶点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,点P运动时△PAD的面积y(cm2)随时间x(s)变化的关系如图2,则a的值为 .
【变式11-3】(2022·开州期中)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
知识点小结:
一、菱形的性质
1.菱形的定义:有一组邻边相等的平行四边形叫做菱形.
2.菱形的性质:①菱形具有平行四边形的所有性质;
②菱形的四条边相等;
③菱形的对角线互相垂直,且菱形的每一条对角线平分它的一组对角;
④菱形既是轴对称图形,也是中心对称图形,对称轴有两条,分别是两条对角线所在的直线,对称中心是两条对角线的交点.
3.菱形的面积:①同平行四边形的面积(底×高);②对角线乘积的一半.(常用等面积法求菱形的高)
二、菱形的判定
1.菱形的判定定理:①一组邻边相等的平行四边形是菱形;
②对角线互相垂直的平行四边形是菱形;
③四边相等的四边形是菱形.
考点总结
【考点1 利用菱形的性质和判定求角度】
【例1】(2022·驻马店期中)如图,在菱形ABCD中,∠ABC=76°,BA=BE,则∠BEA的度数为( )
A.68° B.70° C.71° D.75°
【变式1-1】(2022·绍兴中考)在菱形ABCD中,∠DAB=40°,连接AC,以点A为圆心,AC长为半径作弧,交直线AD于点E,连接CE,则∠AEC的度数是 .
【变式1-2】(2023·廊坊三模)如图,已知在菱形ABCD中,连接对角线AC,作BC边的垂直平分线EF,分别交BC、AC、AD于点F、Q、E,若∠EQD=21°,则∠CAB的度数是( )
A.33° B.37° C.42° D.49°
【变式1-3】(2023·襄阳一模)如图,在ABCD中,AB=AD,点E是AB上一点,连接CE、DE,且BC=CE,若∠BCE=40°则∠ADE= .
【考点2 利用菱形的性质和判定求线段长】
【例2】(2022·郑州期末)如图,在菱形ABCD中,AB=4,按以下步骤作图:①分别以点C和点D为圆心,大于CD的长为半径画弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则BE的值为 .
【变式2-1】(2023·阜阳二模)如图,在菱形ABCD中,对角线AC与BD交于点O,在BD上取一点E,使得DE=AD,连接AE,若BD=16,AE=,则BC的长为 .
【变式2-2】(2023·德州二模)如图,在菱形ABCD中,∠ABC=60°,AB=4,对角线交于点O,F、E分别是AD、OB的中点,则线段EF的长为 .
【变式2-3】(2022·江苏期末)如图,在菱形ABCD中,∠C=60°,AB=2,延长BA至点E,使AE=1,现以点D为圆心,以DE为半径画弧,与直线BC交于点M,则CM的长为 .
【考点3 利用菱形的性质和判定求面积】
【例3】(2022·长宁期末)如图,菱形ABCD的边长为2,∠DAB=60°,连接AC,将菱形ABCD绕点A旋转,使点D的对应点E落在对角线AC上,连接DE,则△DEC的面积是 .
【变式3-1】(2023·聊城中考)如图,在ABCD中,BC的垂直平分线EO交AD于点E,交BC于点O,连接BE,CE,过点C作CF∥BE,交EO的延长线于点F,连接BF.若AD=8,CE=5,则四边形BFCE的面积为 .
【变式3-2】(2022·长沙期中)如图,直线AB与x轴、y轴分别交于A、B两点,点C是OB的中点,D是AB上一点,四边形OEDC是菱形,其中B点坐标为(0,4),∠OAB=30°,则△OAE的面积为 .
【变式3-3】(2022·大庆期末)如图,在菱形ABCD中,∠BAD:∠B=1:3,DE⊥BC于点E,交对角线AC于点P,过点P作PF⊥CD于点F.若△PDF的周长为4,则菱形ABCD的面积为 .
【考点4 利用菱形的性质求点的坐标】
【例4】(2022·烟台期末)如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为 .
【变式4-1】(2023·周口三模)如图,在菱形ABCD中,AB∥y轴,且B(-1,-2),C(3,1),则点D的坐标为 .
【变式4-2】(2023·南京一模)如图,在平面直角坐标系中,菱形OABC的顶点A在y轴上,M、N分别是边OA、OC的中点,若点M,N的纵坐标分别是3,2,则点B的坐标是 .
【变式4-3】(2023·东营中考)如图,在平面直角坐标系中,菱形OABC的边长为,点B在x轴的正半轴上,且∠AOC=60°,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA’B’C’(点A’与点C重合),则点B’的坐标是 .
【考点5 菱形与折叠】
【例5】(2023·江苏)如图,在菱形ABCD中,∠A=100°,E是边AD上的点,沿BE折叠△ABE,点A恰好落在BD上的点F处,连接CF,则∠BFC的度数为( )
A.60° B.70° C.75° D.80°
【变式5-1】(2023·德阳)如图,在菱形纸片ABCD中,∠A=60°,P为AB中点,折叠该纸片使点C落在C’处,且点P在DC’上,折痕为DE,则∠CED的大小为( )
A.55° B.60° C.70° D.75°
【变式5-2】(2022·苏州)如图,菱形纸片ABCD,AB=8,∠B=60°,将该菱形纸片折叠,使点B恰好落在CD边的中点B’处,折痕与边BC、BA分别交于点M、N,则CM的长为 .
【变式5-3】(2020·红桥三模)如图,在边长为4的菱形ABCD中,∠A=60°,点M为AD的中点,连接MC,将菱形ABCD翻折,使点A的对应点E落在MC上,折痕交AB于点N,则线段CE的长度为 .
【考点6 菱形与将军饮马问题(最值)】
【例6】(2021·茂名期中)已知菱形ABCD的两条对角线长分别为10和24,M、N分别是边BC、CD的中点,点P是对角线BD上一动点,则PM+PN的最小值是 .
【变式6-1】(2022·海口)如图,菱形ABCD的面积为,AB=4,点M是AB的中点,点P是对角线AC上的一个动点,则△PBM周长的最小值为 .
【变式6-2】(2023·南阳三模)菱形OABC在平面直角坐标系中的位置如图所示,已知顶点A(8,0),点D是OA的中点,点P是对角线OB上的一个动点,∠AOC=60°,当PA+PD最短时,点P的坐标为 .
【变式6-3】(2022·九年级练习)如图,在菱形ABCD中,AB=5,对角线BD=8.点P、点Q分别是AB、BD上动点,则AQ+PQ的最小值为 .
【考点7 菱形的判定(条件选择)】
【例7】(2020·自贡三模)如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
A.BE⊥CE B.BF∥CE C.BE=CF D.AB=AC
【变式7-1】(2022·蚌埠校考)如图,四边形ABCD的对角线AC与BD相交于点O,OA=OC,OB=OD,添加下列条件仍不能判断四边形ABCD是菱形的是( )
A.BD平分∠ABC B.AC=BD C.AC⊥BD D.AB2=OA2+OB2
【变式7-2】(2023·襄阳模拟)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,且AB∥CD,则添加下列一个条件能判定四边形ABCD是菱形的是( )
A.AC=BD B.∠ADB=∠CDB C.∠ABC=∠DCB D.AD=BC
【变式7-3】(2023·宝鸡二模)如图,在四边形ABCD中,AB=CD,过A作AE⊥BD交BD于点E,过C作CF⊥BD交BD于点F,且AE=CF.请你在不添加辅助线的情况下,添加一个条件 ,使得四边形ABCD是菱形.
【考点8 菱形的性质与判定综合】
【例8】(2022·长治)如图,AE∥BF,∠BAD的平分线交BF于点C,∠ABC的平分线交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AC=6,BD=8,过点D作DH⊥BF于点H,求DH的长.
【变式8-1】(2022·南昌期中)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若AC=4,∠BCF=120°,求菱形BCFE的面积.
【变式8-2】(2021·许昌期中)如图,E和F分别是菱形ABCD的边AB和AD的中点,且AB=15,AC=18,
(1)判断△OEF的形状,并说明理由;
(2)求四边形AEOF的面积.
【变式8-3】(2022·南阳校考)如图,△ABC中,O为AC边的中点,E为OB上一点,过点A作AD∥CE交BO延长线于点D,连接AE、CD.
(1)求证:四边形AECD是平行四边形;
(2)当△ABC满足什么条件时,四边形AECD是菱形?并说明理由;
(3)在(2)的条件下,若CD=5,AC=8,则四边形AECD的面积为 .
【考点9 菱形与中点四边形】
【例9】(2021·临沂期末)我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.下列四边形的中点四边形是菱形的是( )
A.任意四边形 B.等腰梯形 C.平行四边形 D.对角线互相垂直的四边形
【变式9-1】(2022·珠海期中)如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为菱形,则应添加的条件是( )
A.AB∥CD B.AD=BC C.AC⊥BD D.AC=BD
【变式9-2】(2022·静海期中)如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,请你添加一个条件 ,使得四边形EFGH是菱形.
【变式9-3】(2022·泰州校考)如图,四边形ABCD中,AB与CD不平行,E、F、G、H分别是AD、BC、BD、AC的中点,当四边形ABCD满足 时,有EF⊥GH.
【考点10 菱形中的多结论问题】
【例10】(2022·哈尔滨期中)如图,菱形ABCD中,∠A=60°,E、F分别为边AB、AD的中点,DE与BF相交于点G,连接CG,以下结论:①∠BGD=120°;②S△ADE:S△GBC=2:3;③BG+DG=CG;④S菱形ABCD=AB2.其中正确的结论有( )个
A.1 B.2 C.3 D.4
【变式10-1】(2022·泰安期末)如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上一点,且DE=CD,连接BE,分别交AC、AD于点F、G,连接OG.则下列结论:①OG=AB;②由点A、B、D、E构成的四边形是菱形;③S四边形ODGF=S△ABF;④S△ACD=4S△BOG.其中正确结论的个数有( )个
A.1 B.2 C.3 D.4
【变式10-2】(2022·滨州期中)如图,ABCD的对角线AC,BD相交于点O,点E为BC边的中点,连接EO并延长交AD于点F,∠ABC=60°,BC=2AB.下列结论:①SABCD=AB·AC;②AD=4EO;③EF⊥AC;④S△BOE=S△ABC.其中正确结论的个数有( )个
A.1 B.2 C.3 D.4
【变式10-3】(2022·孝感期中)如图,在菱形ABCD中,连接AC,AB=AC,点E、F分别是AB、BC上的点,且AE=BF,连接AF、CE交于点H,连接DH交AC于点O.则下列结论:①AF=CE;②∠CHF=60°;③△ACE≌△BAF;④若AB=1,则S菱形ABCD=.其中正确的个数是( )
A.1 B.2 C.3 D.4
【考点11 菱形中的动点问题】
【例11(2022·龙岩)如图1,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x,△ABP的面积为y,把y看作x的函数,函数的图象如图2所示,则图2中的a等于( )
A.12 B.20 C.24 D.25
【变式11-1】(2023·齐齐哈尔三模)如图①,点F从菱形ABCD的顶点A出发,沿A→B→D以1cm/s的速度匀速运动到点D,图②是点F运动时△FCD的面积y(cm2)随时间x(s)的关系图象,则a的值为 .
【变式11-2】(2023·苏州一模)如图1,点P从菱形ABCD的顶点A出发,沿A→C→B以1cm/s的速度匀速运动到点B,点P运动时△PAD的面积y(cm2)随时间x(s)变化的关系如图2,则a的值为 .
【变式11-3】(2022·开州期中)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
