2023年7月山西省普通高中学业水平考试模拟数学试题(含解析)
文档属性
| 名称 | 2023年7月山西省普通高中学业水平考试模拟数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 832.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-05 20:45:32 | ||
图片预览




文档简介
2023年7月山西省普通高中学业水平考试模拟
数学试题
(考试时间:120分钟 试卷满分:150分)
一 选择题(本大题共12小题,每小题5分,共60分)
1.已知集合,则( )
A. B. C. D.
2.( )
A. B. C. D.
3.命题“”的否定为( )
A. B.
C. D.
4.已知向量,则( )
A. B. C. D.
5.已知函数是定义域为的奇函数,当时,,则( )
A.1 B.-1 C.5 D.-5
6.函数的最小值为( )
A. B.2 C. D.4
7.某学校新建的天文观测台可看作一个球体,其半径为.现要在观测台的表面涂一层防水漆,若每平方米需用涂料,则共需要涂料(单位:)( )
A. B. C. D.
8.已知,则( )
A.1 B.2 C. D.
9.的值是( )
A.1 B. C. D.2
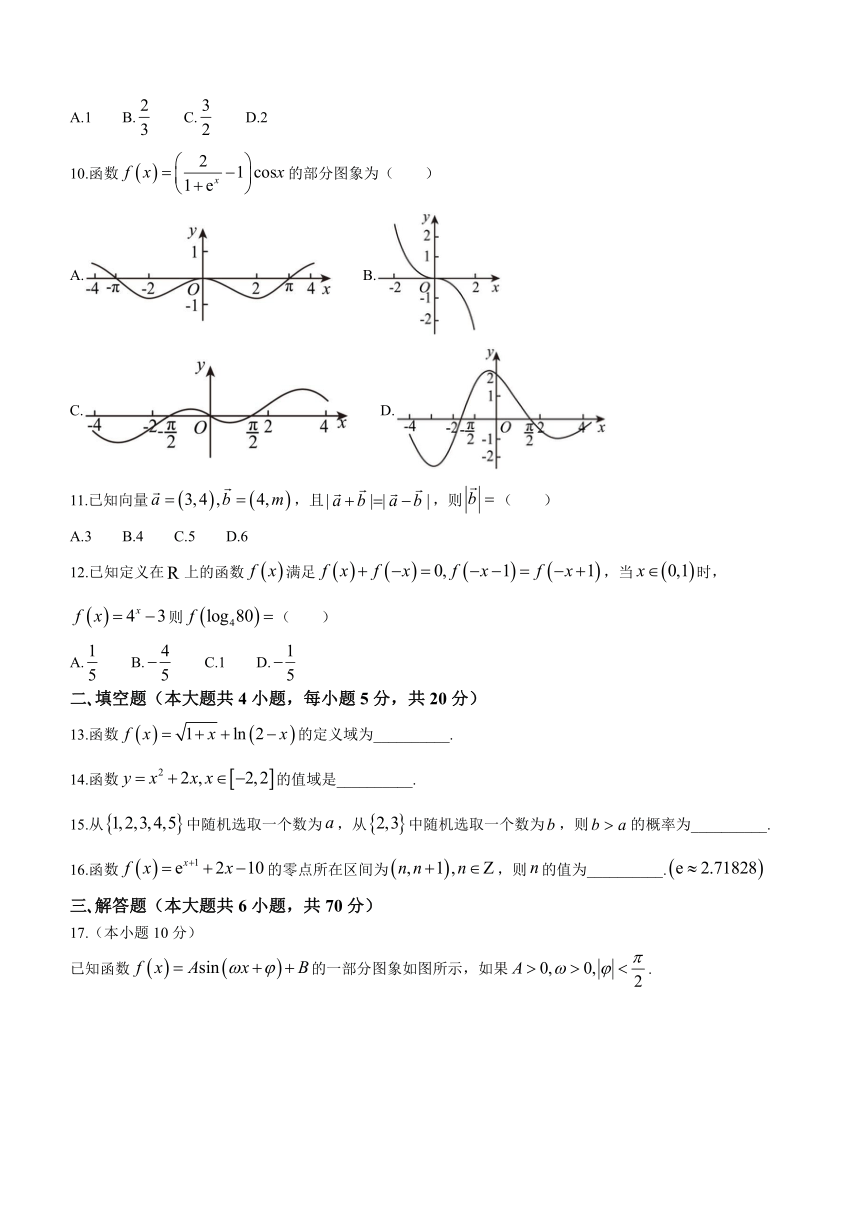
10.函数的部分图象为( )
A. B.
C. D.
11.已知向量,且,则( )
A.3 B.4 C.5 D.6
12.已知定义在上的函数满足,当时,则( )
A. B. C.1 D.
二 填空题(本大题共4小题,每小题5分,共20分)
13.函数的定义域为__________.
14.函数的值域是__________.
15.从中随机选取一个数为,从中随机选取一个数为,则的概率为__________.
16.函数的零点所在区间为,则的值为__________.
三 解答题(本大题共6小题,共70分)
17.(本小题10分)
已知函数的一部分图象如图所示,如果.
(1)求函数的解析式;
(2)当时,求函数的取值范围.
18.(本小题12分)
某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如下图所示.
(1)求的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在的居民中随机抽取8人,则在的居民有多少人.
19.(本小题12分)
已知箱子内有6张大小相同的卡片,其中2张金卡,4张银卡,从中不放回地依次随机抽取2张,求下列事件的概率
(1)“第二次抽到金卡”;
(2)“至少抽到一次金卡”.
20.(本小题12分)
在中,.
(1)求的面积;
(2)求及的值.
21.(本小题12分)
如图,在四棱锥中,四边形是菱形,为的中点.求证:
(1)平面;
(2)平面平面.
22.(本小题12分)
当前新冠肺炎疫情防控形势依然严峻,要求每个公民对疫情防控都不能放松.科学使用防护用品是减少公众交叉感染 有效降低传播风险 防止疫情扩散蔓延 确保群众身体健康的有效途径.某疫情防护用品生产厂家年投入固定成本150万元,每生产万件,需另投入成本(万元).当年产量不足60万件时,;当年产量不小于60万件时,.通过市场分析,若每万件售价为400万元时,该厂年内生产的防护用品能全部售完.(利润=销售收入一总成本)
(1)求出年利润(万元)关于年产量(万件)的解析式;
(2)年产量为多少万件时,该厂在这一防护用品生产中所获利润最大?并求出利润的最大值.
参考答案:
1.A
【分析】直接利用并集的定义求解.
【详解】因为集合,
所以.
故选:A
2.C
【分析】利用复数的四则运算即可得解.
【详解】.
故选:C.
3.B
【分析】根据特称量词命题的否定为全称量词命题判断即可.
【详解】命题“”为特称量词命题,
其否定为:.
故选:B
4.D
【分析】根据平面向量的坐标运算可得.
【详解】因为,所以.
故选:D
5.B
【分析】利用奇函数性质可得,将代入相应解析式计算即可.
【详解】根据奇函数性质可知;
而,所以,
所以.
故选:B
6.D
【分析】利用基本不等式运算求解.
【详解】,则,
,当且仅当,即时,等号成立,
故函数的最小值为4.
故选:D.
7.D
【分析】先利用球的表面积公式求出表面积,再根据条件即可求出结果.
【详解】因为,所以球的表面积为,又每平方米需用涂料,所以共需涂料.
故选:D
8.B
【分析】利用两角差的正切公式即可求解.
【详解】根据两角差的正切公式可得;
解得.
故选:B
9.B
【分析】根据换底公式的结论运算求解.
【详解】由题意可得:.
故选:B.
10.C
【分析】由函数的奇偶性,特值法求解即可.
【详解】,
所以,
所以为奇函数,故排除;
当时,,故排除;
故选:C.
11.C
【分析】根据,两边平方后可得,求出的值,进而求出
【详解】,两边平方得,
展开整理得.
,解得.
故选:C
12.D
【分析】根据所给的等式可得为奇函数且周期为2,再根据对数的运算求解即可.
【详解】由可得为奇函数,又,则,故,故周期为2.
故
.
故选:D
13.
【分析】根据函数解析式有意义可得出关于的不等式组,由此可解得函数的定义域.
【详解】对于函数,有,解得.
故函数的定义域为.
故答案为:.
14.
【分析】配方得,根据二次函数的性质即可求解.
【详解】,
故当时,;当时,.
故函数的值域是.
故答案为:.
15.
【分析】先求出基本事件的总数15,再由列举法求出包含的基本事件的个数,由此能求出的概率.
【详解】从中随机选取一个数为,从中随机选取一个数为,
基本事件的总数,
则包含的基本事件有:,共3个,
的概率是.
故答案为:.
16.1
【分析】利用零点存在性定理以及函数的单调性求得正确答案.
【详解】在上递增,
,
所以的零点在区间,
所以的值为1.
故答案为:1
17.(1)
(2)
【分析】(1)由函数的最大值和最小值求出,由周期求出,由特殊点求出,即可求得函数解析式;
(2)由求出的范围,再求出的取值范围,即可求得函数的取值范围.
【详解】(1)由图象可知,,
设最小正周期为,
,
又,且,
,
函数的解析式为.
(2)当时,,
函数的取值范围是.
18.(1)
(2)3360元
(3)6
【分析】(1)根据直方图中频率和为1列方程求参数;
(2)根据直方图计算平均值;
(3)根据分层抽样的等比例性质求在的居民数量.
【详解】(1)依题意,,解得.
(2)所有受灾居民经济损失的平均值为
元.
(3)由(1)得经济损失在和在的人数比例为,
由分层抽样知,经济损失在的居民有人.
19.(1)
(2)
【分析】用列举法写出基本事件空间,利用古典概型公式直接得解.
【详解】(1)将2张金卡编号为张银卡编号为,
从中不放回地依次随机抽取2张,
所有的可能有,,,共30种,
其中满足事件A的有,共10种,
所以;
(2)满足事件的有,,共18种,
所有.
20.(1)
(2)
【分析】(1)利用平方关系求得,应用三角形面积公式求的面积;
(2)余弦公式求,再应用正弦定理求.
【详解】(1)由且,则,
所以.
(2)由,则,
而,则.
21.(1)证明见解析
(2)证明见解析
【分析】(1)设,连接,根据中位线可得,再根据线面平行的判定定理即可证明;
(2)根据可得,根据四边形为菱形,可得,再根据线面垂直的判断定理可得平面,再根据面面垂直的判定定理即可得出结果.
【详解】(1)设,连接,如图所示:
因为分别为的中点,所以,
又因为平面平面,
所以平面.
(2)连接,如图所示:
因为为的中点,所以,
又因为四边形为菱形,所以,
因为平面平面,且,
所以平面,又因为平面,
所以平面平面.
22.(1)
(2)当年产量为90万件时,该厂在这一防护商品生产中所获利润最大为1050万元
【分析】(1)根据题意直接利用利润=销售收入-总成本,写出分段函数的解析式即可;
(2)利用二次函数及其基本不等式分别求出各段的最大值,再取两个最大的即可.
【详解】(1)当且时,
,
当且时,
综上:
(2)当且时,
当时,取最大值(万元)
当且时,
当且仅当,即时等号成立.
当时,取最大值万元)
,
综上所述,当年产量为90万件时,该厂在这一防护商品生产中所获利润最大为1050万元.
数学试题
(考试时间:120分钟 试卷满分:150分)
一 选择题(本大题共12小题,每小题5分,共60分)
1.已知集合,则( )
A. B. C. D.
2.( )
A. B. C. D.
3.命题“”的否定为( )
A. B.
C. D.
4.已知向量,则( )
A. B. C. D.
5.已知函数是定义域为的奇函数,当时,,则( )
A.1 B.-1 C.5 D.-5
6.函数的最小值为( )
A. B.2 C. D.4
7.某学校新建的天文观测台可看作一个球体,其半径为.现要在观测台的表面涂一层防水漆,若每平方米需用涂料,则共需要涂料(单位:)( )
A. B. C. D.
8.已知,则( )
A.1 B.2 C. D.
9.的值是( )
A.1 B. C. D.2
10.函数的部分图象为( )
A. B.
C. D.
11.已知向量,且,则( )
A.3 B.4 C.5 D.6
12.已知定义在上的函数满足,当时,则( )
A. B. C.1 D.
二 填空题(本大题共4小题,每小题5分,共20分)
13.函数的定义域为__________.
14.函数的值域是__________.
15.从中随机选取一个数为,从中随机选取一个数为,则的概率为__________.
16.函数的零点所在区间为,则的值为__________.
三 解答题(本大题共6小题,共70分)
17.(本小题10分)
已知函数的一部分图象如图所示,如果.
(1)求函数的解析式;
(2)当时,求函数的取值范围.
18.(本小题12分)
某地区突发小型地质灾害,为了了解该地区受灾居民的经济损失,制定合理的帮扶方案,研究人员经过调查后将该地区所有受灾居民的经济损失情况统计如下图所示.
(1)求的值;
(2)求所有受灾居民的经济损失的平均值;
(3)现按照分层抽样的方法从经济损失在的居民中随机抽取8人,则在的居民有多少人.
19.(本小题12分)
已知箱子内有6张大小相同的卡片,其中2张金卡,4张银卡,从中不放回地依次随机抽取2张,求下列事件的概率
(1)“第二次抽到金卡”;
(2)“至少抽到一次金卡”.
20.(本小题12分)
在中,.
(1)求的面积;
(2)求及的值.
21.(本小题12分)
如图,在四棱锥中,四边形是菱形,为的中点.求证:
(1)平面;
(2)平面平面.
22.(本小题12分)
当前新冠肺炎疫情防控形势依然严峻,要求每个公民对疫情防控都不能放松.科学使用防护用品是减少公众交叉感染 有效降低传播风险 防止疫情扩散蔓延 确保群众身体健康的有效途径.某疫情防护用品生产厂家年投入固定成本150万元,每生产万件,需另投入成本(万元).当年产量不足60万件时,;当年产量不小于60万件时,.通过市场分析,若每万件售价为400万元时,该厂年内生产的防护用品能全部售完.(利润=销售收入一总成本)
(1)求出年利润(万元)关于年产量(万件)的解析式;
(2)年产量为多少万件时,该厂在这一防护用品生产中所获利润最大?并求出利润的最大值.
参考答案:
1.A
【分析】直接利用并集的定义求解.
【详解】因为集合,
所以.
故选:A
2.C
【分析】利用复数的四则运算即可得解.
【详解】.
故选:C.
3.B
【分析】根据特称量词命题的否定为全称量词命题判断即可.
【详解】命题“”为特称量词命题,
其否定为:.
故选:B
4.D
【分析】根据平面向量的坐标运算可得.
【详解】因为,所以.
故选:D
5.B
【分析】利用奇函数性质可得,将代入相应解析式计算即可.
【详解】根据奇函数性质可知;
而,所以,
所以.
故选:B
6.D
【分析】利用基本不等式运算求解.
【详解】,则,
,当且仅当,即时,等号成立,
故函数的最小值为4.
故选:D.
7.D
【分析】先利用球的表面积公式求出表面积,再根据条件即可求出结果.
【详解】因为,所以球的表面积为,又每平方米需用涂料,所以共需涂料.
故选:D
8.B
【分析】利用两角差的正切公式即可求解.
【详解】根据两角差的正切公式可得;
解得.
故选:B
9.B
【分析】根据换底公式的结论运算求解.
【详解】由题意可得:.
故选:B.
10.C
【分析】由函数的奇偶性,特值法求解即可.
【详解】,
所以,
所以为奇函数,故排除;
当时,,故排除;
故选:C.
11.C
【分析】根据,两边平方后可得,求出的值,进而求出
【详解】,两边平方得,
展开整理得.
,解得.
故选:C
12.D
【分析】根据所给的等式可得为奇函数且周期为2,再根据对数的运算求解即可.
【详解】由可得为奇函数,又,则,故,故周期为2.
故
.
故选:D
13.
【分析】根据函数解析式有意义可得出关于的不等式组,由此可解得函数的定义域.
【详解】对于函数,有,解得.
故函数的定义域为.
故答案为:.
14.
【分析】配方得,根据二次函数的性质即可求解.
【详解】,
故当时,;当时,.
故函数的值域是.
故答案为:.
15.
【分析】先求出基本事件的总数15,再由列举法求出包含的基本事件的个数,由此能求出的概率.
【详解】从中随机选取一个数为,从中随机选取一个数为,
基本事件的总数,
则包含的基本事件有:,共3个,
的概率是.
故答案为:.
16.1
【分析】利用零点存在性定理以及函数的单调性求得正确答案.
【详解】在上递增,
,
所以的零点在区间,
所以的值为1.
故答案为:1
17.(1)
(2)
【分析】(1)由函数的最大值和最小值求出,由周期求出,由特殊点求出,即可求得函数解析式;
(2)由求出的范围,再求出的取值范围,即可求得函数的取值范围.
【详解】(1)由图象可知,,
设最小正周期为,
,
又,且,
,
函数的解析式为.
(2)当时,,
函数的取值范围是.
18.(1)
(2)3360元
(3)6
【分析】(1)根据直方图中频率和为1列方程求参数;
(2)根据直方图计算平均值;
(3)根据分层抽样的等比例性质求在的居民数量.
【详解】(1)依题意,,解得.
(2)所有受灾居民经济损失的平均值为
元.
(3)由(1)得经济损失在和在的人数比例为,
由分层抽样知,经济损失在的居民有人.
19.(1)
(2)
【分析】用列举法写出基本事件空间,利用古典概型公式直接得解.
【详解】(1)将2张金卡编号为张银卡编号为,
从中不放回地依次随机抽取2张,
所有的可能有,,,共30种,
其中满足事件A的有,共10种,
所以;
(2)满足事件的有,,共18种,
所有.
20.(1)
(2)
【分析】(1)利用平方关系求得,应用三角形面积公式求的面积;
(2)余弦公式求,再应用正弦定理求.
【详解】(1)由且,则,
所以.
(2)由,则,
而,则.
21.(1)证明见解析
(2)证明见解析
【分析】(1)设,连接,根据中位线可得,再根据线面平行的判定定理即可证明;
(2)根据可得,根据四边形为菱形,可得,再根据线面垂直的判断定理可得平面,再根据面面垂直的判定定理即可得出结果.
【详解】(1)设,连接,如图所示:
因为分别为的中点,所以,
又因为平面平面,
所以平面.
(2)连接,如图所示:
因为为的中点,所以,
又因为四边形为菱形,所以,
因为平面平面,且,
所以平面,又因为平面,
所以平面平面.
22.(1)
(2)当年产量为90万件时,该厂在这一防护商品生产中所获利润最大为1050万元
【分析】(1)根据题意直接利用利润=销售收入-总成本,写出分段函数的解析式即可;
(2)利用二次函数及其基本不等式分别求出各段的最大值,再取两个最大的即可.
【详解】(1)当且时,
,
当且时,
综上:
(2)当且时,
当时,取最大值(万元)
当且时,
当且仅当,即时等号成立.
当时,取最大值万元)
,
综上所述,当年产量为90万件时,该厂在这一防护商品生产中所获利润最大为1050万元.
同课章节目录
