九年级上学期数学分类题型汇编 【圆】第1节【圆的有关性质】
文档属性
| 名称 | 九年级上学期数学分类题型汇编 【圆】第1节【圆的有关性质】 |  | |
| 格式 | zip | ||
| 文件大小 | 308.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-20 09:59:44 | ||
图片预览

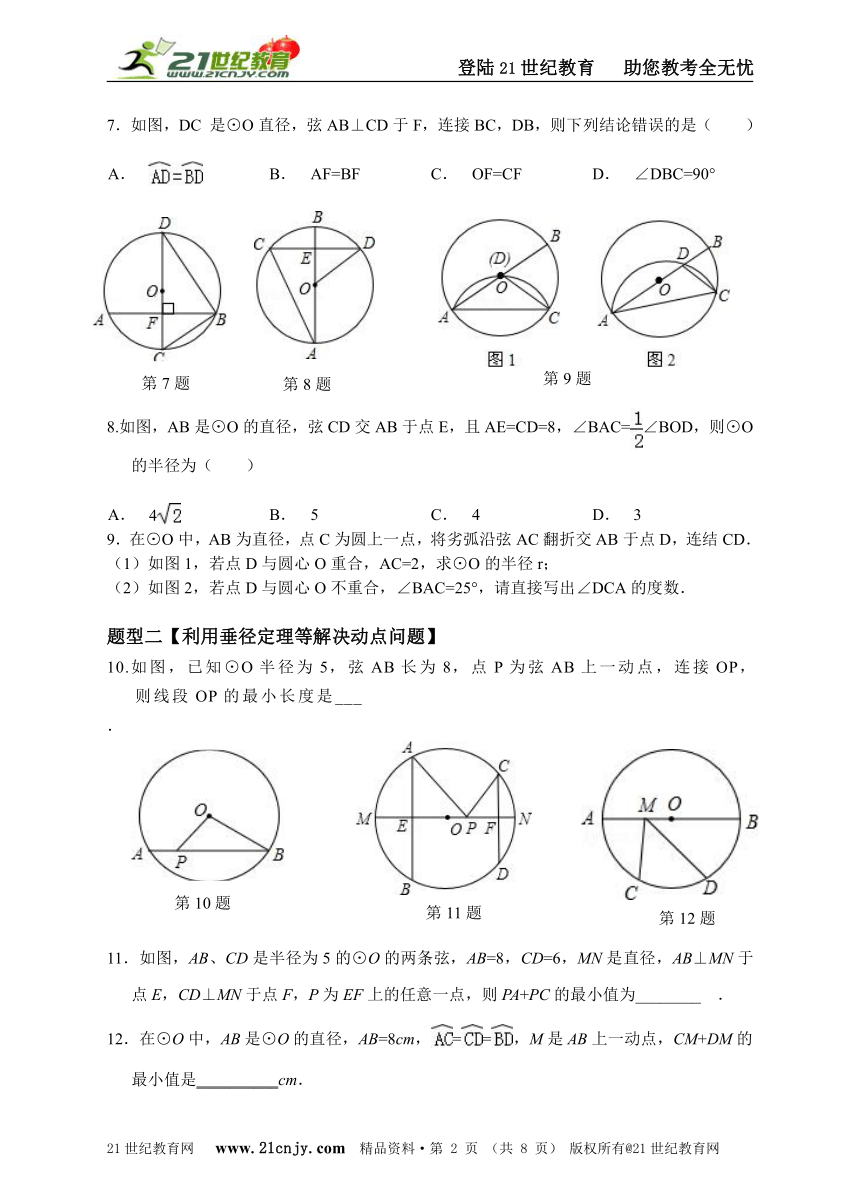

文档简介
九上数学分类题型汇编 【圆】第1节【圆的有关性质】
题型一【利用垂径定理及推论求半径或弦长等】
1.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )21教育网
A.2 B.8 C.2 D.2
2.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为( )21世纪教育网版权所有
A.4 B.5 C.4 D.3
3.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
4.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( ) 21*cnjy*com
A.
cm
B.
cm
C.
cm或cm
D.
cm或cm
5.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A.
3
B.
3
C.
D.
6.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( ).2·1·c·n·j·y
A. B. C. D.
7.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.
AF=BF
C.
OF=CF
D.
∠DBC=90°
8.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为( )2-1-c-n-j-y
A.
4
B.
5
C.
4
D.
3
9.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
题型二【利用垂径定理等解决动点问题】
10.如图,已知⊙O半径为5,弦AB长为8,点P为弦AB上一动点,连接OP,则线段OP的最小长度是___21教育名师原创作品
.
11.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为________ .
12.在⊙O中,AB是⊙O的直径,AB=8cm,==,M是AB上一动点,CM+DM的最小值是__________cm.
13.在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为 .
14.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为 .
15.已知如图,⊙O的直径为10,弦AB=8,P是弦AB上一个动点,则OP长的取值范围为( )
A.OP<5 B.8<OP<10 C.3<OP<5 D.3≤OP≤5
题型三 【垂径定理的实际应用】
16.如图,在直径为130mm的圆铁片上切去一块高为32mm的弓形铁片.求这个弓形铁片弦AB的长.
17.今有一圆木砌入壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问径几何?(一尺为10寸)
18.如图是一个汽油桶的截面图,其上方有一个进油孔,该汽油桶的截面直径为50dm,此时汽油桶内液面宽度AB=40dm,现在从进油孔处倒油,当液面AB=48dm时,液面上升__dm.21cnjy.com
19.绍兴市著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A.
4m
B.
5m
C.
6m
D.
8m
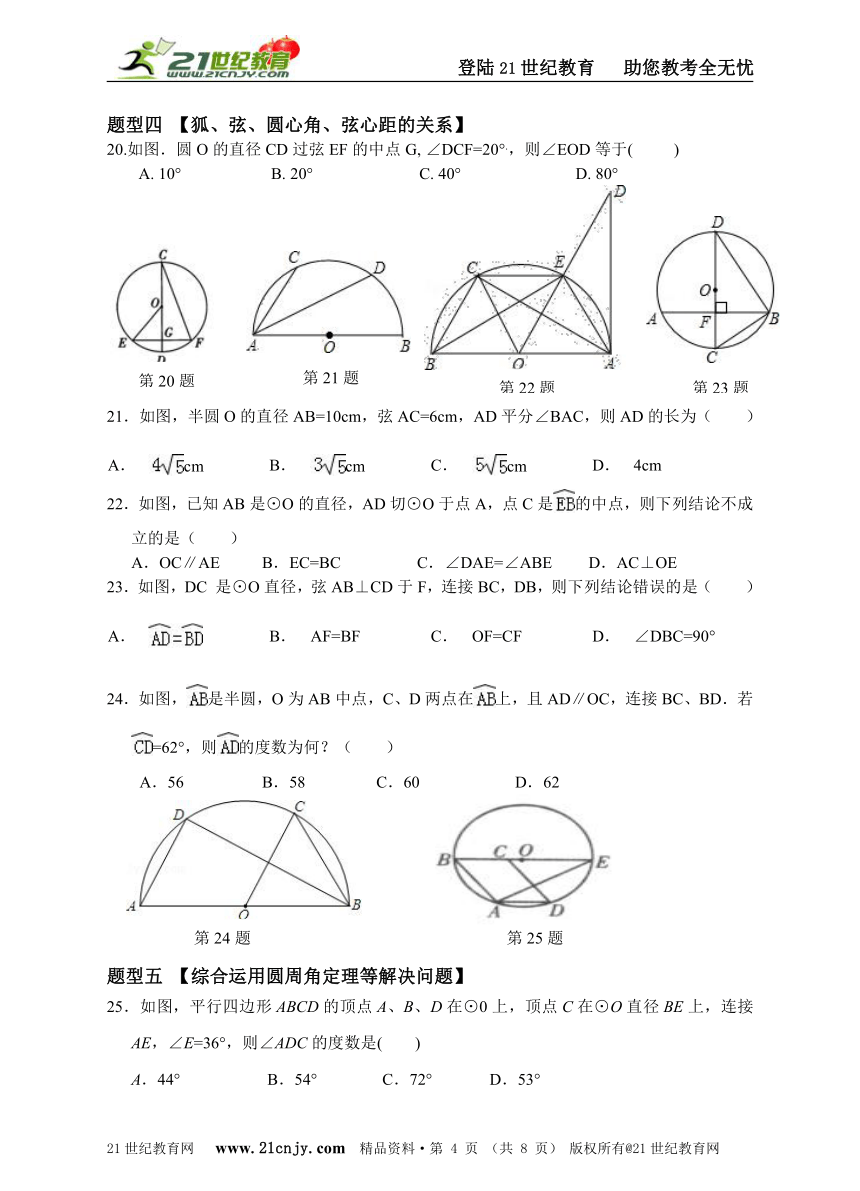
题型四 【狐、弦、圆心角、弦心距的关系】
20.如图.圆O的直径CD过弦EF的中点G, ∠DCF=20°.,则∠EOD等于( )
A. 10° B. 20° C. 40° D. 80°
21.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.
cm
B.
cm
C.
cm
D.
4cm
22.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
23.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.
AF=BF
C.
OF=CF
D.
∠DBC=90°
24.如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )21·cn·jy·com
A.56 B.58 C.60 D.62
题型五 【综合运用圆周角定理等解决问题】
25.如图,平行四边形ABCD的顶点A、B、D在⊙0上,顶点C在⊙O直径BE上,连接AE,∠E=36°,则∠ADC的度数是( )www.21-cn-jy.com
A.44° B.54° C.72° D.53°
26.如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A. 25° B. 50° C. 60° D. 80°
27.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.
AE=BE
B.
=
C.
OE=DE
D.
∠DBC=90°
28.如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是 .
29.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于 .【来源:21·世纪·教育·网】
30.如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )21·世纪*教育网
A.36° B.46° C.27° D.63°
31.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .
32.如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4 B. C.6 D.
33.如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )www-2-1-cnjy-com
A.
3
B.
4
C.
5
D.
8
34.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )【来源:21cnj*y.co*m】
A.
2
B.
8
C.
2
D.
2
35.如图,OC是⊙O的半径,AB是弦,且OC⊥AB,点P在⊙O上,∠APC=26°,则∠BOC=_________ 度.【出处:21教育名师】
36.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是 度.
37.在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .【版权所有:21教育】
题型六 【构造圆内接四边形求角度】
38.如图,圆心角∠AOB=120°,P是狐AB上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于( )21*cnjy*com
A.45° B.60° C.75° D.85°
39.如图,等边△ABC内接于⊙O,P是狐AB上任一点(点P不与点A、B重合),连AP、BP,过点C作C21世纪教育网M∥BP交PA的延长线于点M.
(1)填空:∠APC=____度,∠BPC=________度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求梯形PBCM的面积.
参考答案
D
B
B
C
C
D
C
B
(1) (2) 40°
3
8
24
10
D
112.mm
26寸
8或22
D
C
A
D
C
A
B
B
C
70°
36°
A
2
B
C
D
52°
144°
(0,12)或(0,﹣12)
B
解答:(1)解:∠APC=60°,∠BPC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°-∠BPM=180°-(∠APC+∠BPC)=180°-120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PBC=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
∴△ACM≌△BCP;
(3)解:作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+PB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=
∴S梯形PBCM=(PB+CM)×PH=
题型一【利用垂径定理及推论求半径或弦长等】
1.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )21教育网
A.2 B.8 C.2 D.2
2.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为( )21世纪教育网版权所有
A.4 B.5 C.4 D.3
3.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
4.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( ) 21*cnjy*com
A.
cm
B.
cm
C.
cm或cm
D.
cm或cm
5.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A.
3
B.
3
C.
D.
6.如图,⊙O的直径AB=12,CD是⊙O的弦,CD⊥AB,垂足为P,且BP:AP=1:5,则CD的长为( ).2·1·c·n·j·y
A. B. C. D.
7.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.
AF=BF
C.
OF=CF
D.
∠DBC=90°
8.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为( )2-1-c-n-j-y
A.
4
B.
5
C.
4
D.
3
9.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
题型二【利用垂径定理等解决动点问题】
10.如图,已知⊙O半径为5,弦AB长为8,点P为弦AB上一动点,连接OP,则线段OP的最小长度是___21教育名师原创作品
.
11.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为________ .
12.在⊙O中,AB是⊙O的直径,AB=8cm,==,M是AB上一动点,CM+DM的最小值是__________cm.
13.在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为 .
14.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为 .
15.已知如图,⊙O的直径为10,弦AB=8,P是弦AB上一个动点,则OP长的取值范围为( )
A.OP<5 B.8<OP<10 C.3<OP<5 D.3≤OP≤5
题型三 【垂径定理的实际应用】
16.如图,在直径为130mm的圆铁片上切去一块高为32mm的弓形铁片.求这个弓形铁片弦AB的长.
17.今有一圆木砌入壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问径几何?(一尺为10寸)
18.如图是一个汽油桶的截面图,其上方有一个进油孔,该汽油桶的截面直径为50dm,此时汽油桶内液面宽度AB=40dm,现在从进油孔处倒油,当液面AB=48dm时,液面上升__dm.21cnjy.com
19.绍兴市著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A.
4m
B.
5m
C.
6m
D.
8m
题型四 【狐、弦、圆心角、弦心距的关系】
20.如图.圆O的直径CD过弦EF的中点G, ∠DCF=20°.,则∠EOD等于( )
A. 10° B. 20° C. 40° D. 80°
21.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.
cm
B.
cm
C.
cm
D.
4cm
22.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
23.如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是( )
A.
B.
AF=BF
C.
OF=CF
D.
∠DBC=90°
24.如图,是半圆,O为AB中点,C、D两点在上,且AD∥OC,连接BC、BD.若=62°,则的度数为何?( )21·cn·jy·com
A.56 B.58 C.60 D.62
题型五 【综合运用圆周角定理等解决问题】
25.如图,平行四边形ABCD的顶点A、B、D在⊙0上,顶点C在⊙O直径BE上,连接AE,∠E=36°,则∠ADC的度数是( )www.21-cn-jy.com
A.44° B.54° C.72° D.53°
26.如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A. 25° B. 50° C. 60° D. 80°
27.如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A.
AE=BE
B.
=
C.
OE=DE
D.
∠DBC=90°
28.如图,已知A、B、C三点在⊙O上,AC⊥BO于D,∠B=55°,则∠BOC的度数是 .
29.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=54°,则∠BAC的度数等于 .【来源:21·世纪·教育·网】
30.如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )21·世纪*教育网
A.36° B.46° C.27° D.63°
31.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .
32.如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为( )
A.4 B. C.6 D.
33.如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为( )www-2-1-cnjy-com
A.
3
B.
4
C.
5
D.
8
34.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )【来源:21cnj*y.co*m】
A.
2
B.
8
C.
2
D.
2
35.如图,OC是⊙O的半径,AB是弦,且OC⊥AB,点P在⊙O上,∠APC=26°,则∠BOC=_________ 度.【出处:21教育名师】
36.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒,点E在量角器上对应的读数是 度.
37.在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为 .【版权所有:21教育】
题型六 【构造圆内接四边形求角度】
38.如图,圆心角∠AOB=120°,P是狐AB上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于( )21*cnjy*com
A.45° B.60° C.75° D.85°
39.如图,等边△ABC内接于⊙O,P是狐AB上任一点(点P不与点A、B重合),连AP、BP,过点C作C21世纪教育网M∥BP交PA的延长线于点M.
(1)填空:∠APC=____度,∠BPC=________度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求梯形PBCM的面积.
参考答案
D
B
B
C
C
D
C
B
(1) (2) 40°
3
8
24
10
D
112.mm
26寸
8或22
D
C
A
D
C
A
B
B
C
70°
36°
A
2
B
C
D
52°
144°
(0,12)或(0,﹣12)
B
解答:(1)解:∠APC=60°,∠BPC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°-∠BPM=180°-(∠APC+∠BPC)=180°-120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PBC=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
∴△ACM≌△BCP;
(3)解:作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+PB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=
∴S梯形PBCM=(PB+CM)×PH=
同课章节目录
