点和圆的位置关系

“136”导学案——九年级数学（上）
编号： 班级： 姓名：
课题：点和圆的位置关系
主备： 审核： 时间：2014年 7 月 日
一、明确学习目标
1、理解并掌握：点和圆的三种位置关系。
2、理解不在同一直线上的三个点确定一个圆并掌握它的运用。
3、了解三角形的外接圆和三角形外心的概念。
4、了解反证法的证明思想。
二、自主预习
预习教材第92至94页，完成自主预习区中的练习。
三、合作探究
【小组讨论】
问题1 点和圆的三种位置关系？(圆的半径为r，点P与圆心的距离为d）
【学生展示】
【师生互评】略
问题2 按下列条件作圆
（1）作经过已知点A的圆，这样的圆能作多少个？
（2）经过A、B两点作圆，这样的圆能作出多少个？它们的圆心分布有什么特点？
（3）经过A、B、C三点作圆，有哪些情况？三点应符合什么条件才能作圆？
[学生讨论]讨论、操作、交流后完成。
【教师小结】（1）无数个，圆心可以在任何 ( http: / / www.21cnjy.com )位置；（2）无数个，圆心在连接两点线段的中垂线上；（3）不在同一条直线上的任意三个点可以作唯一一个圆，圆心在连接任意两点的线段的中垂线的交点处。
问题3 什么叫三角形的外接圆？三角形有外心及性质？
问题4 教材是如何用反证法证明过同一直线上的三点不能作圆？
反证法的证明思路是什么？
学生回答、互评、教师小结
1、三角形外接圆定义及圆内接三角形之间的关系。
2、外心的定义及性质：三角形三边中垂线的交点；外心到三顶点距离相等。
3、反证法的证题“三步曲”：①假设，②推出矛盾，③否定假设，肯定结论。
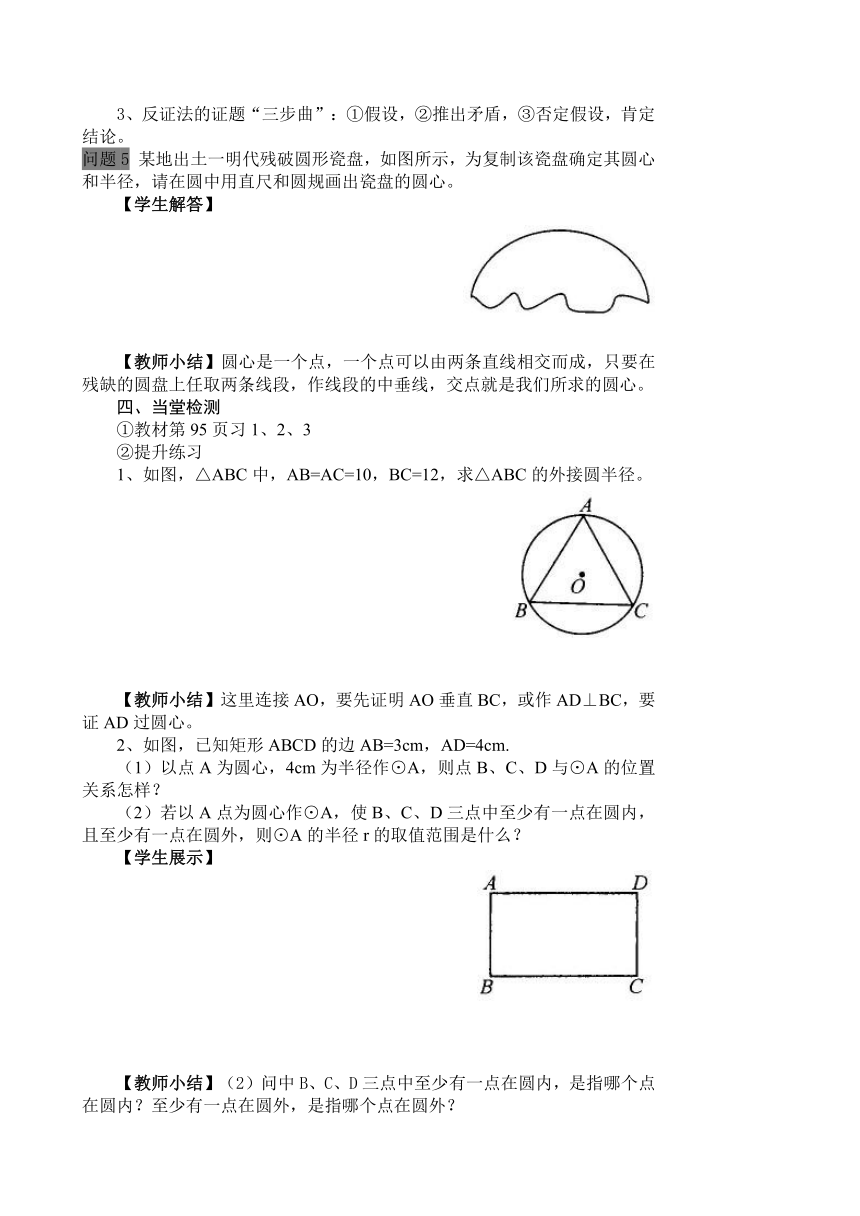
问题5 某地出土一明代残破圆形瓷盘，如图所示，为复制该瓷盘确定其圆心和半径，请在圆中用直尺和圆规画出瓷盘的圆心。
【学生解答】
【教师小结】圆心是一个点，一个点可以由两条直线相交而成，只要在残缺的圆盘上任取两条线段，作线段的中垂线，交点就是我们所求的圆心。
四、当堂检测
①教材第95页习1、2、3
②提升练习
1、如图，△ABC中，AB=AC=10，BC=12，求△ABC的外接圆半径。
【教师小结】这里连接AO，要先证明AO垂直BC，或作AD⊥BC，要证AD过圆心。
2、如图，已知矩形ABCD的边AB=3cm，AD=4cm.
（1）以点A为圆心，4cm为半径作⊙A，则点B、C、D与⊙A的位置关系怎样？
（2）若以A点为圆心作⊙A，使B、C、D三点中至少有一点在圆内，且至少有一点在圆外，则⊙A的半径r的取值范围是什么？
【学生展示】
【教师小结】（2）问中B、C、D三点中至少有一点在圆内，是指哪个点在圆内？至少有一点在圆外，是指哪个点在圆外？
五、拓展提升
( http: / / www.21cnjy.com )
六、课后作业
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )