湖南省湘潭市湘潭县2022-2023学年八年级下学期期末数学试题(无答案)
文档属性
| 名称 | 湖南省湘潭市湘潭县2022-2023学年八年级下学期期末数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 837.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 10:44:36 | ||
图片预览


文档简介
2023年上学期期末考试试卷
八年级数学
一、选择题(本大题共8个小题,每小题3分,满分24分)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A. B. C. D.
2.若点在第二象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.一个正多边形的内角和与外角和之比为,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
4.下列各组数中,是勾股数的是( )
A.8,24,25 B.8,15,17 C.10.20,26 D.14,36,39
5.如图正方形ABCD和正方形EFGO的边长都是1,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积( )
A. B. C. D.不能确定
6.对某班一次考试成绩进行统计,其中一组的频数是7,频率是0.2,那么该班级的人数是( )人.
A.7个 B.14个 C.35个 D.70个
7.我国汉代数学家赵爽为了证明勾股定理,创制了弦图,后人称为“赵爽弦图”,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,如图,若,,则EF的长是( ).
A.5 B.7 C. D.12
8.如图,在正方形ABCD中,,点E,F分别在边AB,CD上,.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为( )
A.1 B. C. D.2
二、多选题(本大题共4个小题,每小题3分,共12分.在每小题给出的4个选项中,有多项符合题目要求.全部选对的得3分,部分选对的得2分,有选错的得0分)
9.如图,在中,,点D是AB边上的中点.下列结论正确的有( )
A. B.
C. D.
10.下列说法错误的是( )
A.平行四边形既是轴对称图形又是中心对称图形 B.三个角是直角的四边形是矩形
C.三条边相等的四边形是菱形 D.矩形的对角线垂直平分,菱形的对角线平分相等
11.一次函数的图象大致是( )
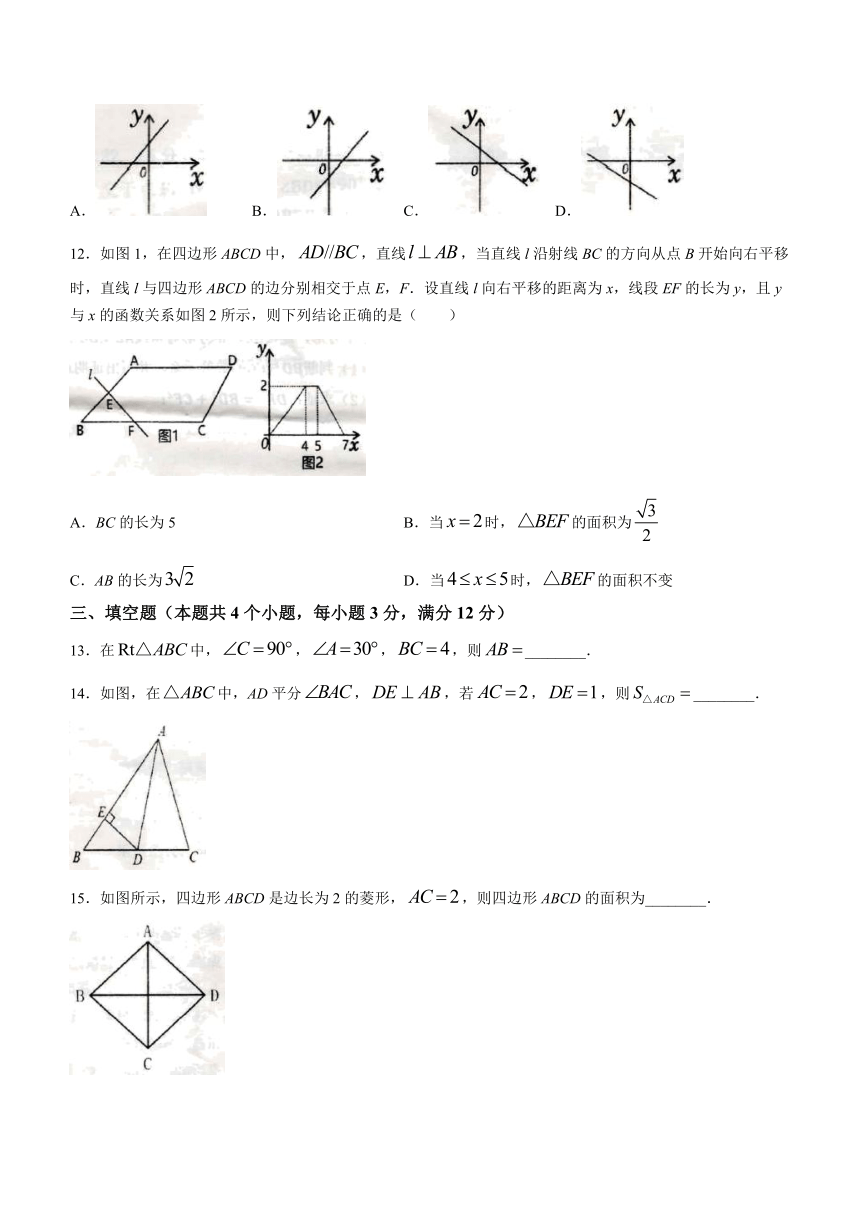
A. B. C. D.
12.如图1,在四边形ABCD中,,直线,当直线l沿射线BC的方向从点B开始向右平移时,直线l与四边形ABCD的边分别相交于点E,F.设直线l向右平移的距离为x,线段EF的长为y,且y与x的函数关系如图2所示,则下列结论正确的是( )
A.BC的长为5 B.当时,的面积为
C.AB的长为 D.当时,的面积不变
三、填空题(本题共4个小题,每小题3分,满分12分)
13.在中,,,,则________.
14.如图,在中,AD平分,,若,,则________.
15.如图所示,四边形ABCD是边长为2的菱形,,则四边形ABCD的面积为________.
16.如图,直线与x轴交于点,与直线交于点,则方程组的解是________.
四、解答题(72分)
17.(6分)如图,每个小正方形网格的边长表示50米,A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)请你以学校为坐标原点,正东方向为x轴正方向,正北方向为y轴的正方向,在图中建立平面直角坐标系;
(2)利用(1)中建立的平面直角坐标系,写出B同学家的坐标,若C同学家的坐标为,请在图上标出C同学家的位置.
18.(6分)已知A,B两艘船同时从港口O出发,船A以的速度向东航行;船B以的速度向北航行.它们离开港口后,相距多远?
19.(6分)如图,的对角线AC,BD相交于点O,且E、F、G、H分别是OA、OB、OC、OD的中点.求证:四边形EFGH是平行四边形.
20.(6分)已知,如图,直线与直线.
(1)写出两直线与y轴交点A,B的坐标;
(2)求两直线交点C的坐标.
21.(6分)某校八年级学生进行了一次视力调查,绘制出频数分布表和频数直方图的一部分如下.请根据图表信息回答下列问题:
视力 频数(人) 频率
20 0.1
40 0.2
70 0.35
a 0.3
10 b
(每组数据含最小值,不含最大值)
(1)在频数分布表中,a的值为________,b的值为________.
(2)将频数直方图补充完整;
(3)眼科医生建议,视力低于4.6需要佩戴眼镜,该中学3000人,请估算戴眼镜的学生大概有多少?
22.(6分)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,.
(1)求证:四边形ABDF是矩形;
(2)若,,求的面积.
23.(8分)某数学学习小组在学习《勾股定理》之后进行了拓展研究,类比勾股定理,新定义一种三第角形,规定:如果一个三角形两边的平方和等于第三边平方的2倍,那么称这个三角形为“奇异勾股三角形”,请根据“奇异勾股三角形”的定义,完成下列问题:
(1)判断:下列说法正确的是________(填甲、乙、丙)
组员甲说:等边三角形一定是“奇异勾股三角形”;
组员乙说:等腰直角三角形也是“奇异勾股三角形”;
组员丙说:三边长分别为,2,的三角形也是“奇异勾股三角形”.
(2)若是“奇异勾股三角形”.且两边长分别为1,,求第三边的长;
(3)若是“奇异勾股三角形”,且三边长分别a,b,c(a,b为直角边,c为斜边,且).求的周长(用只含有a的式子表示).
24.(8分)某医药生产厂家研制了一种新药,经临床试验发现,成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(h)而变化的情况如图所示.
(1)写出与时,y与x之间的函数表达式;
(2)当成人每毫升血液中含药量为3微克以上时,他服药已经多长时间了?
(3)研究表明,当血液中含药量(微克)时,对治疗疾病有效,则有效时间多长?
25.(10分)如图,已知中,,,点D为边BC上一动点,四边形ADEG是正方形,连接GC,正方形对角线AE交BC于点F.
(1)判断BD与CG的数量关系,并写出证明过程;
(2)求证:;
(3)若,求AE的值.
26(10分)如图,平面直角坐标系中,,,,,直线经过点A,且与y轴交于D点.
(1)求点A、点B的坐标;
(2)试说明:;
(3)若点M是直线AD上的一个动点,在x轴上是否存在另一个点N,使以O,B,M,N为顶点的四边形是平行四边形?请直接写出点N的坐标.
八年级数学
一、选择题(本大题共8个小题,每小题3分,满分24分)
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A. B. C. D.
2.若点在第二象限,则点一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.一个正多边形的内角和与外角和之比为,则这个多边形的边数为( )
A.5 B.6 C.7 D.8
4.下列各组数中,是勾股数的是( )
A.8,24,25 B.8,15,17 C.10.20,26 D.14,36,39
5.如图正方形ABCD和正方形EFGO的边长都是1,正方形EFGO绕点O旋转时,两个正方形重叠部分的面积( )
A. B. C. D.不能确定
6.对某班一次考试成绩进行统计,其中一组的频数是7,频率是0.2,那么该班级的人数是( )人.
A.7个 B.14个 C.35个 D.70个
7.我国汉代数学家赵爽为了证明勾股定理,创制了弦图,后人称为“赵爽弦图”,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,如图,若,,则EF的长是( ).
A.5 B.7 C. D.12
8.如图,在正方形ABCD中,,点E,F分别在边AB,CD上,.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为( )
A.1 B. C. D.2
二、多选题(本大题共4个小题,每小题3分,共12分.在每小题给出的4个选项中,有多项符合题目要求.全部选对的得3分,部分选对的得2分,有选错的得0分)
9.如图,在中,,点D是AB边上的中点.下列结论正确的有( )
A. B.
C. D.
10.下列说法错误的是( )
A.平行四边形既是轴对称图形又是中心对称图形 B.三个角是直角的四边形是矩形
C.三条边相等的四边形是菱形 D.矩形的对角线垂直平分,菱形的对角线平分相等
11.一次函数的图象大致是( )
A. B. C. D.
12.如图1,在四边形ABCD中,,直线,当直线l沿射线BC的方向从点B开始向右平移时,直线l与四边形ABCD的边分别相交于点E,F.设直线l向右平移的距离为x,线段EF的长为y,且y与x的函数关系如图2所示,则下列结论正确的是( )
A.BC的长为5 B.当时,的面积为
C.AB的长为 D.当时,的面积不变
三、填空题(本题共4个小题,每小题3分,满分12分)
13.在中,,,,则________.
14.如图,在中,AD平分,,若,,则________.
15.如图所示,四边形ABCD是边长为2的菱形,,则四边形ABCD的面积为________.
16.如图,直线与x轴交于点,与直线交于点,则方程组的解是________.
四、解答题(72分)
17.(6分)如图,每个小正方形网格的边长表示50米,A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)请你以学校为坐标原点,正东方向为x轴正方向,正北方向为y轴的正方向,在图中建立平面直角坐标系;
(2)利用(1)中建立的平面直角坐标系,写出B同学家的坐标,若C同学家的坐标为,请在图上标出C同学家的位置.
18.(6分)已知A,B两艘船同时从港口O出发,船A以的速度向东航行;船B以的速度向北航行.它们离开港口后,相距多远?
19.(6分)如图,的对角线AC,BD相交于点O,且E、F、G、H分别是OA、OB、OC、OD的中点.求证:四边形EFGH是平行四边形.
20.(6分)已知,如图,直线与直线.
(1)写出两直线与y轴交点A,B的坐标;
(2)求两直线交点C的坐标.
21.(6分)某校八年级学生进行了一次视力调查,绘制出频数分布表和频数直方图的一部分如下.请根据图表信息回答下列问题:
视力 频数(人) 频率
20 0.1
40 0.2
70 0.35
a 0.3
10 b
(每组数据含最小值,不含最大值)
(1)在频数分布表中,a的值为________,b的值为________.
(2)将频数直方图补充完整;
(3)眼科医生建议,视力低于4.6需要佩戴眼镜,该中学3000人,请估算戴眼镜的学生大概有多少?
22.(6分)如图,在平行四边形ABCD中,连接BD,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,.
(1)求证:四边形ABDF是矩形;
(2)若,,求的面积.
23.(8分)某数学学习小组在学习《勾股定理》之后进行了拓展研究,类比勾股定理,新定义一种三第角形,规定:如果一个三角形两边的平方和等于第三边平方的2倍,那么称这个三角形为“奇异勾股三角形”,请根据“奇异勾股三角形”的定义,完成下列问题:
(1)判断:下列说法正确的是________(填甲、乙、丙)
组员甲说:等边三角形一定是“奇异勾股三角形”;
组员乙说:等腰直角三角形也是“奇异勾股三角形”;
组员丙说:三边长分别为,2,的三角形也是“奇异勾股三角形”.
(2)若是“奇异勾股三角形”.且两边长分别为1,,求第三边的长;
(3)若是“奇异勾股三角形”,且三边长分别a,b,c(a,b为直角边,c为斜边,且).求的周长(用只含有a的式子表示).
24.(8分)某医药生产厂家研制了一种新药,经临床试验发现,成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(h)而变化的情况如图所示.
(1)写出与时,y与x之间的函数表达式;
(2)当成人每毫升血液中含药量为3微克以上时,他服药已经多长时间了?
(3)研究表明,当血液中含药量(微克)时,对治疗疾病有效,则有效时间多长?
25.(10分)如图,已知中,,,点D为边BC上一动点,四边形ADEG是正方形,连接GC,正方形对角线AE交BC于点F.
(1)判断BD与CG的数量关系,并写出证明过程;
(2)求证:;
(3)若,求AE的值.
26(10分)如图,平面直角坐标系中,,,,,直线经过点A,且与y轴交于D点.
(1)求点A、点B的坐标;
(2)试说明:;
(3)若点M是直线AD上的一个动点,在x轴上是否存在另一个点N,使以O,B,M,N为顶点的四边形是平行四边形?请直接写出点N的坐标.
同课章节目录
