3.6 弧长及扇形面积的计算

课件14张PPT。13.6 弧长及扇形面积的计算21.经历探索弧长计算公式及扇形面积计算公式的过程，培养学生的探索能力．
2.了解弧长及扇形面积公式后，能用公式解决问题，训练学生的数学运用能力．3 在田径二百米跑比赛中，每位运动员的起跑位置相同吗？每位运动员弯路的展直长度相同吗？4（1）半径为R的圆,周长是多少？C=2πR （3）1°圆心角所对弧长是多少？ （4）140°圆心角所对的弧长是多少？（2）圆的周长可以看作是多少度的圆心角所对的弧？n°ABO若设⊙O半径为R，n°的圆心角
所对的弧长为 π5【例1】如图所示为一段弯形管道，其中心线是一段圆弧 .已知 的圆心为O，半径OA=60cm，∠AOB=108°，求这段弯管的长度(精确到0.1cm)61.已知弧所对的圆心角为90°，半径是4，则弧长为____
2. 已知一条弧的半径为9，弧长为8 ，那么这条弧所对的圆心角为_______.
3. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
B. C. D.
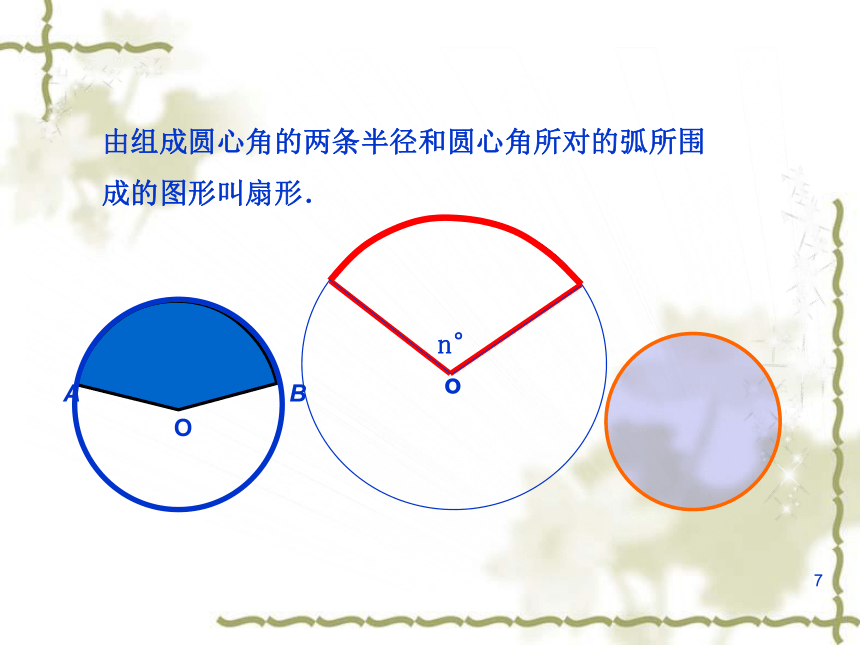
160°B7由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形．8（1）半径为R的圆,面积是多少？S=πR2 （3）1°圆心角所对扇形面积是多少？ （2）圆面可以看作是多少度的圆心角所对的扇形？若设⊙O半径为R， n°的圆心角所对的扇形面积为S，则 9O比较扇形面积与弧长公式, 用弧长表示扇形面积:10如图 一把扇形纸扇完全打开后，外侧两竹条AB与AC的夹角为120°，AB的长为30cm，竹条AB上贴纸部分BD的宽为20cm.求扇子的一面上贴纸部分的面积（精确到0.1cm2）.解 由图可知，扇形的圆心为A，圆心角n=120 °，AB=30cm，BD=20cm，图上贴纸部分的面积等于两个扇形面积之差，由扇形的面积公式，贴纸部分的面积为111、已知扇形的圆心角为120°，半径为2，则这个扇形的面积S扇形=____.2、已知扇形面积为 ，圆心角为60°，则这个扇形的半径R=____． 3、已知半径为2的扇形，其弧长为 ，则这个扇形的面积S扇形=____．121. 如图，已知□ABCD的对角线BD=4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（ ） A．4π cm B．3π cm C．2π cm D．π cm
【解析】选C. 点D所转过的路径是以O为圆心OD为半径，圆心角180°的弧长。133.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚
(如图),那么B点从开始至B2结束所走过的路径长度_______.BB1B2F'B1BABCDEFB2141.弧长的计算公式l＝ 并运用公式进行计算；
2.扇形的面积公式S＝ 并运用公式进行计算；
3.弧长l及扇形的面积S之间的关系，并能已知一方
求另一方．通过本课时的学习，需要我们掌握：