2.2 30°,45°,60°角的三角比课件
文档属性
| 名称 | 2.2 30°,45°,60°角的三角比课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 831.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-21 00:00:00 | ||
图片预览



文档简介
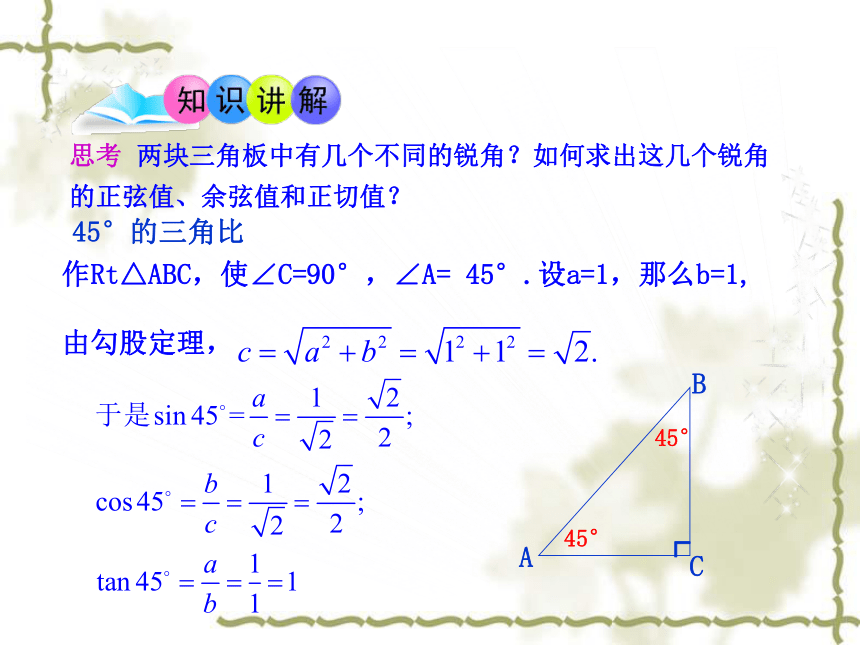
课件17张PPT。ABCcba┌2.2 30°,45°,60°角的三角比 1.能推导并熟记30°、45°、60°角的三角函数值,并能根据这些值说出对应锐角度数;
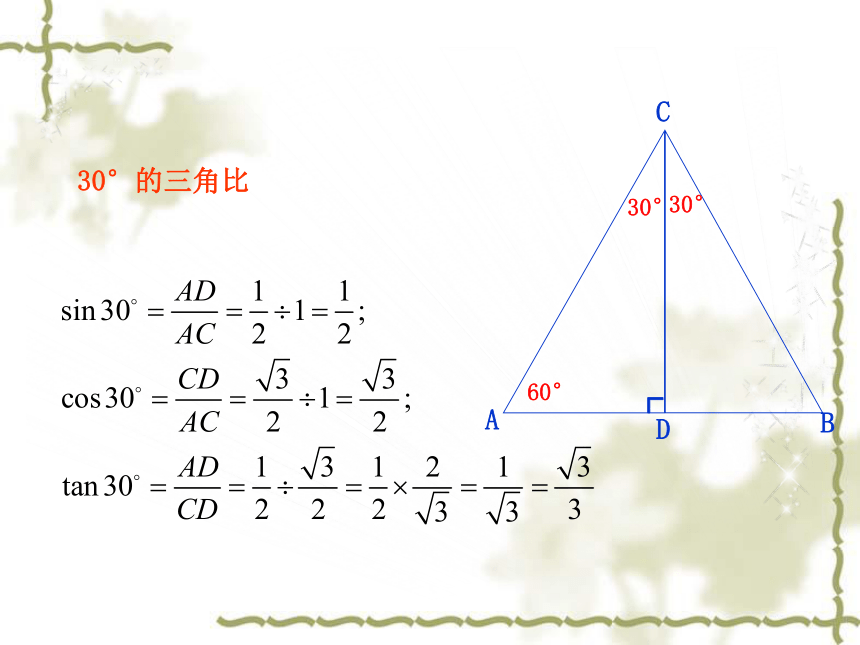
2.能熟练计算含有30°、45°、60°角的三角函数的运算式. AB C∠A的对边∠A的邻边斜边思考 两块三角板中有几个不同的锐角?如何求出这几个锐角的正弦值、余弦值和正切值?45°的三角比┌45°45°ABC作Rt△ABC,使∠C=90°,∠A= 45°.设a=1,那么b=1,
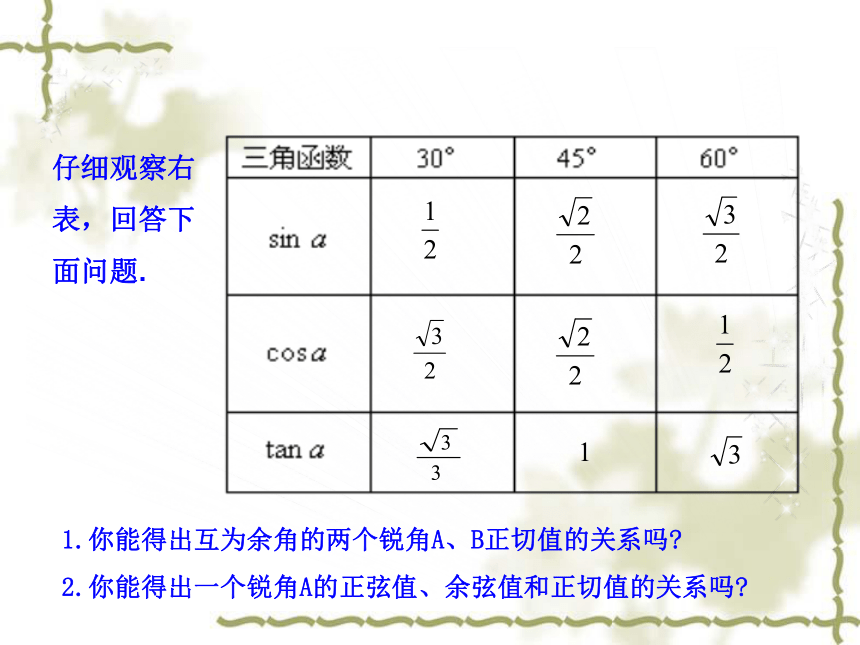
由勾股定理,┌30°60°30°ABCD30°的三角比1.你能得出互为余角的两个锐角A、B正切值的关系吗?
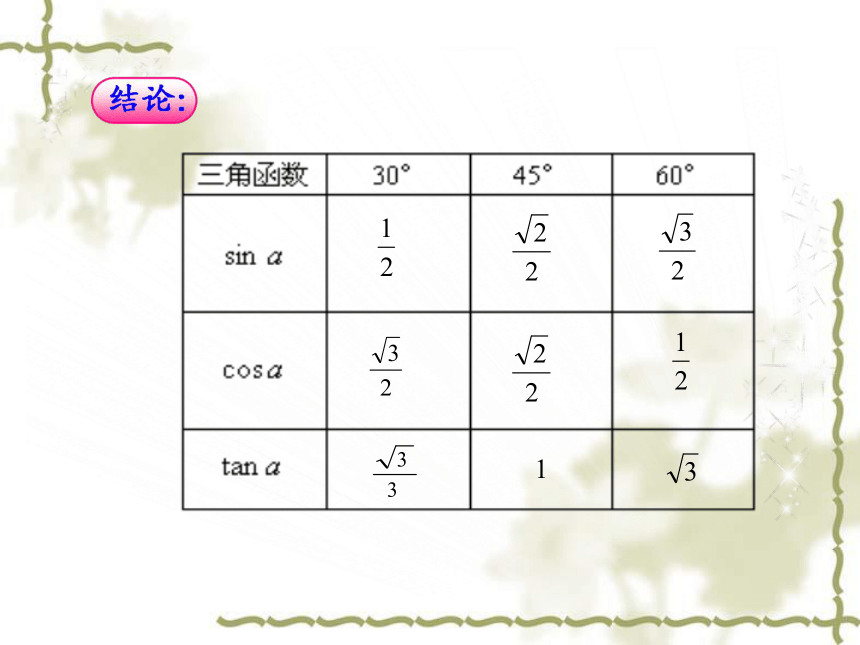
2.你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?仔细观察右表,回答下面问题.sinA=cos(90°?∠A);
一个锐角的正弦值等于这个角余角的余弦值.
cosA=sin(90°?∠A);
一个锐角的余弦值等于这个角余角的正弦值.
tanA·tan(90°?∠A)=1.
一个锐角的正切值与这个角余角的正切值互为倒数.【例】求下列各式的值.
(1)cos260°+sin260°sin260°表示(sin60°)2,即sin60°·sin60°.【解析】(1)cos260°+sin260°
=( )2+( )2 = ÷ -1=0.=1;当A、B为锐角时,若A≠B,则 sinA≠sinB,cosA≠cosB,tanA≠tanB.(2)1.cos30°=( )
A. B. C. D. 【解析】选C.由三角函数的定义知cos30°=2. 计算 的结果等于( )
【答案】选B.3. 如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB= ,则下底BC的长为
__________.【答案】104. 计算:【解析】 5.已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值;
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.∴cos∠ACB=cos30°=【解析】(1)∵∠B=60°,∴∠BCD=60°,又 ∵AB=AD=DC,∴∠DAC=∠DCA,∵AD∥BC,∴∠DAC=∠BCA,∴∠DCA=∠BCA∴∠ACB=30°(2)AB=AD=DC=8,∠ACB=30°, ∴BC=2AB=16,∵E,F 分别是AB,DC 的中点,【规律方法】1.记住30°,45 °,60 °的特殊值,及推导方式,可以提高计算速度.2.会构造直角三角形,充分利用勾股定理的有关知识结合三角函数灵活运用.直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
2.能熟练计算含有30°、45°、60°角的三角函数的运算式. AB C∠A的对边∠A的邻边斜边思考 两块三角板中有几个不同的锐角?如何求出这几个锐角的正弦值、余弦值和正切值?45°的三角比┌45°45°ABC作Rt△ABC,使∠C=90°,∠A= 45°.设a=1,那么b=1,
由勾股定理,┌30°60°30°ABCD30°的三角比1.你能得出互为余角的两个锐角A、B正切值的关系吗?
2.你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?仔细观察右表,回答下面问题.sinA=cos(90°?∠A);
一个锐角的正弦值等于这个角余角的余弦值.
cosA=sin(90°?∠A);
一个锐角的余弦值等于这个角余角的正弦值.
tanA·tan(90°?∠A)=1.
一个锐角的正切值与这个角余角的正切值互为倒数.【例】求下列各式的值.
(1)cos260°+sin260°sin260°表示(sin60°)2,即sin60°·sin60°.【解析】(1)cos260°+sin260°
=( )2+( )2 = ÷ -1=0.=1;当A、B为锐角时,若A≠B,则 sinA≠sinB,cosA≠cosB,tanA≠tanB.(2)1.cos30°=( )
A. B. C. D. 【解析】选C.由三角函数的定义知cos30°=2. 计算 的结果等于( )
【答案】选B.3. 如图,已知梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB= ,则下底BC的长为
__________.【答案】104. 计算:【解析】 5.已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
(1)求cos∠ACB的值;
(2)若E,F分别是AB,DC的中点,连接EF,求线段EF的长.∴cos∠ACB=cos30°=【解析】(1)∵∠B=60°,∴∠BCD=60°,又 ∵AB=AD=DC,∴∠DAC=∠DCA,∵AD∥BC,∴∠DAC=∠BCA,∴∠DCA=∠BCA∴∠ACB=30°(2)AB=AD=DC=8,∠ACB=30°, ∴BC=2AB=16,∵E,F 分别是AB,DC 的中点,【规律方法】1.记住30°,45 °,60 °的特殊值,及推导方式,可以提高计算速度.2.会构造直角三角形,充分利用勾股定理的有关知识结合三角函数灵活运用.直角三角形三边的关系.
直角三角形两锐角的关系.
直角三角形边与角之间的关系.
特殊角30°,45°,60°角的三角函数值.
互余两角之间的三角函数关系.
同角之间的三角函数关系
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
