2.1 锐角三角比课件

课件18张PPT。2.1 锐角三角比
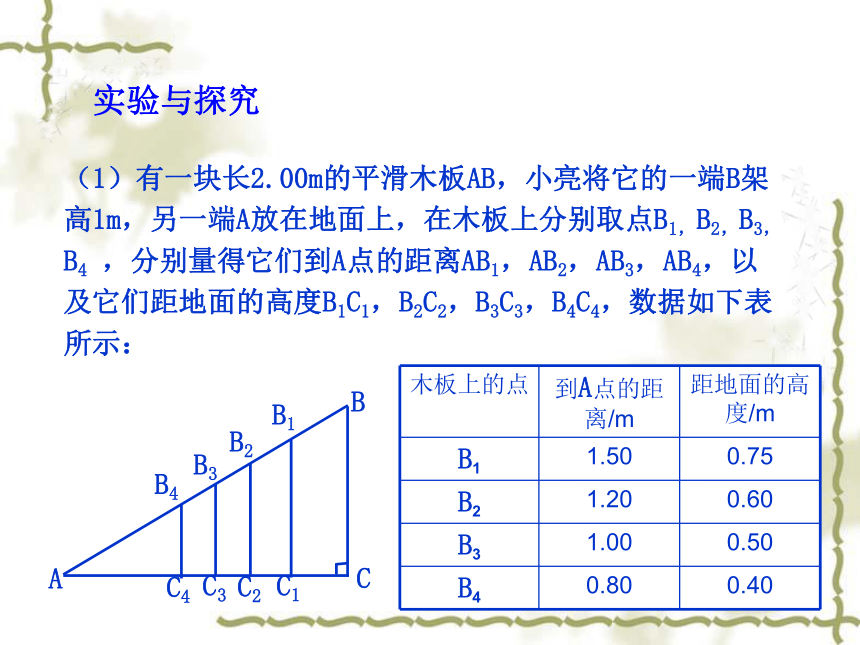
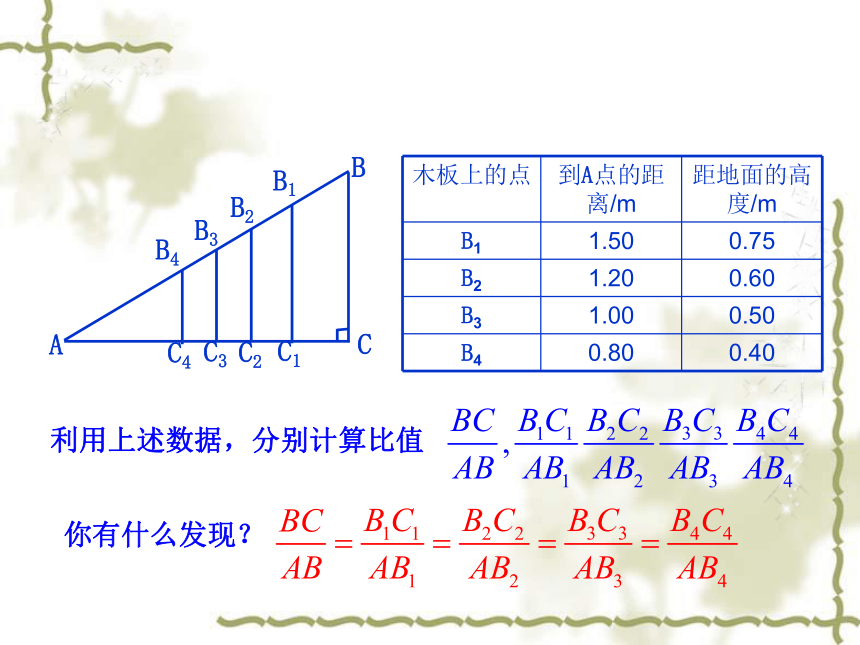
第2章 解直角三角形 实验与探究（1）有一块长2.00m的平滑木板AB，小亮将它的一端B架高1m，另一端A放在地面上，在木板上分别取点B1，B2，B3，B4 ，分别量得它们到A点的距离AB1，AB2，AB3，AB4，以及它们距地面的高度B1C1，B2C2，B3C3，B4C4，数据如下表所示： 利用上述数据，分别计算比值你有什么发现？任意画Rt△ABC和Rt△A′B′C′，使得∠C＝∠C′＝
90°，∠A＝∠A′＝α，那么 与 有什么关
系．你能解释一下吗？ABCA'B'C'两个三角形相似，对应边成比例，故比值相等.αα 这就是说，在直角三角形中，当锐角A 的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比也是一个固定值．如图，在Rt△ABC中，∠C＝90°，我们把锐角A的对边与斜边的比叫做∠A的正弦，记作sinA．即例如，当∠A＝30°时，我们有当∠A＝45°时，我们有cab对边斜边1.理解当直角三角形的锐角固定时，它的对边与斜边的比值都固定（即正弦值不变）这一事实；
2.理解锐角三角比的概念，记住三角比的符号. 当直角三角形的一个锐角的大小确定时，其任意两边的比值都是唯一确定的吗？为什么？我们把∠A的邻边与斜边的比叫
做∠A的余弦，记作cosA，即把∠A的对边与邻边的比叫做∠A的正切，记作tanA，即ACB在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比及对边与邻边的比
是一个固定值.A′B′C′任意画Rt△ABC和Rt△A′B′C′，使得∠C=∠C′=90°，∠A=∠A′=α.那么有什么关系？，及由于∠C=∠C′=90°，∠A=∠A′=α，
所以Rt△ABC∽Rt△A′B′C′，∟BACbca斜边角 的对边∠A的对边记作a，
∠B的对边记作b，
∠C的对边记作c.角A的邻边锐角A的正弦、余弦、正切统称锐角A的三角比 (也叫做锐角A的三角函数).A【例】如图，在Rt△ABC中，∠C=90°，BC=6，sinA= ，
求cosA，tanB的值.【解析】1.判断对错:1)如图① sinA= （ ）
②sinB= （ ）
③sinA=0.6 m （ ）
④sinB=0.8 （ ）√√√×sinA是一个比值，无单位.2)如图，sinA= （ ） ×2.在Rt△ABC中，锐角A的对边和斜边同时扩大100倍，sinA
的值（ ）
A.扩大100倍 B.缩小
C.不变 D.不能确定C3.如图ACB3630°，则sinA=______.1.如图，在△ABC中，∠C=90°, AB=13，BC=5，则sinA的值是（ ）
A. B. C. D.【解析】选A．由正弦的定义可得2. 如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的值为( )
A.2 B． C． D．
【解析】选B.根据正切的函数定义，角A的正切应是它的对边与邻边的比，所以B是正确，A是∠B的正切；C和D都错．3.在平面直角坐标系中,已知点A(3,0)和B(0,-4),C在原点
上，连接三点组成直角三角形ABC,则sin∠CAB等于____.
4.在Rt△ABC中,∠C=90°,AD是BC边上的中线,AC=2,BC=4,
则sin∠DAC=_____.
5.在Rt△ABC中,
则sin∠A=___.ba求一个角的正弦值，除了用定义直接求外，还可以
转化为求和它相等角的正弦值.6.如图, ∠C=90°CD⊥AB.sinB可以由哪两条线段之比?若AC=5,CD=3,求sinB的值.【解析】∵∠B=∠ACD ,∴sinB=sin∠ACD .在Rt△ADC中，AD=sin ∠ACD=∴sinB=