人教版数学七年级上册 3.1 第2课时 等式的性质课件(19张PPT)
文档属性
| 名称 | 人教版数学七年级上册 3.1 第2课时 等式的性质课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 377.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 18:26:03 | ||
图片预览





文档简介
(共19张PPT)
3.1 从算式到方程
第2课时 等式的性质
学习目标
1.理解等式的两条性质
2.会利用等式的性质解简单的一元一次方程
3.培养观察、分析、概括及逻辑思维能力,形成独立思考与合作交流的良好学习习惯
1.像m+n=n+m,x+2x=3x,3×3+1=5×2,3x+1=5y 这样的式子,都是等式;
2.用等号表示相等关系的式子,叫做等式;
3.通常可以用a=b表示一般的等式.
学习回顾
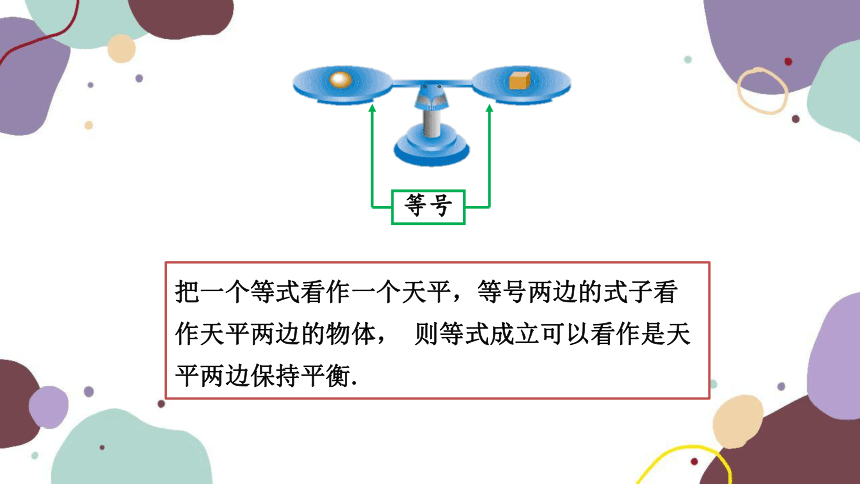
等号
把一个等式看作一个天平,等号两边的式子看作天平两边的物体, 则等式成立可以看作是天平两边保持平衡.
新课导入
(1)3x-5=22;
(2)0.28-0.13y=0.27y+1.
用估算的方法可以求出简单的一元一次方程解.
你能用估算的方法求出下列方程的解吗?
用估算的方法解比较复杂的方程是困难的.
因此,我们要讨论怎样解方程?
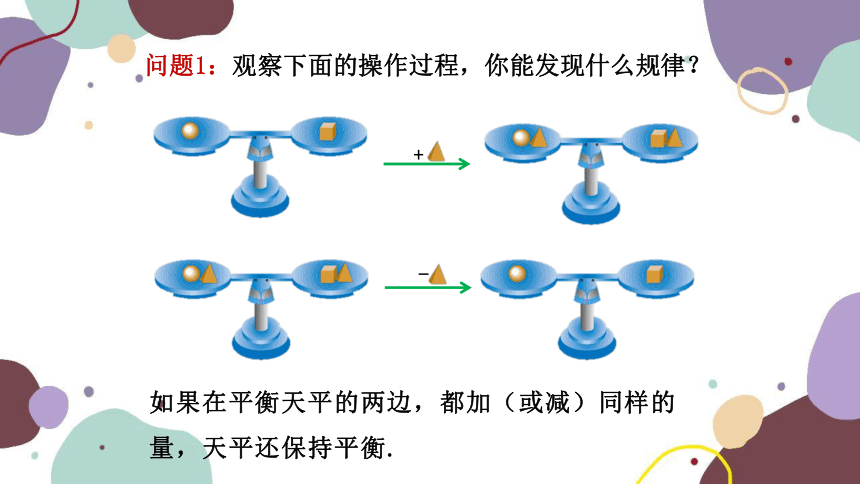
问题1:观察下面的操作过程,你能发现什么规律?
+
-
如果在平衡天平的两边,都加(或减)同样的量,天平还保持平衡.
等式的性质1:
等式两边加(或减)同一个数(或式子), 结果仍相等.
如果a=b,那么a±c=b±c.
问题2:观察下面的操作过程,你能发现什么规律?
×2
×3
天平在 增加 相同倍数重量的物体时,天平仍保持平衡.
÷2
÷3
减少
等式的性质2
等式两边乘同一个数,或除以同一个不等于0的数,结果仍相等.
如果a=b,那么ac=bc;
如果a=b(c ≠ 0),那么
(1)在运用等式的性质时,要特别注意关键词
“两边”和“同一个”,特别是“同一个”.
运用等式的性质时应注意:
(2)在运用等式的性质1时,两边加(或减)的可以是“同一个数”,也可以是“同一个式子”.
(3)在运用等式的性质2时,除以的同一个数不能为“0”,并且不能随便乘或除以“同一个式子”.
例:利用等式的性质解下列方程.
(1)x+7=26;
解:两边减7,得
x = 19.
于是
x+7-7=26-7.
(2)-5x=20;
解:两边除以-5,得
于是
x = -4.
解以x为未知数的方程,就是把方程逐步转化为x=a(a为常数)的形式,等式的性质是转化的重要依据.
解:两边加 5,得
化简,得
两边乘-3,得
x = -27.
(3) ;
将x = -27代入方程的左边,
得
方程的左右两边相等,
所以 x = -27是方程
的解.
检验:
随堂练习
1.下列变形符合等式性质的是( )
A.如果2x-3=7,那么2x=7-3
B.如果3x-2=1,那么3x=1-2
C.如果-2x=5,那么x=5+2
D
2. 下列说法错误的是( )
A.若x=3,则3=x.
B.若x=y,y=z,则x=z.
C.若ab=1,则a= .
D.若2+a=b-3, 则4+2a=2b -3.
D
-6
3. 如果mx=my,那么下列等式中不一定成立的是( )
A.mx+1=my+1
B.mx-3=my-3
C.-mx=-my
D.x=y
D
前提:m≠0
4. 利用等式的性质解下列方程并检验.
(1)5- x=-5;
解:两边减5,得
5- x-5=-5-5.
化简,得
x = -10.
两边除以 ,得
x = 50.
检验:当x = 50时,左边=5- ×50 =-5 =右边.
所以 x=50是原方程的解.
(2) .
解:两边加 ,得 .
化简,得 .
两边除以 ,得 .
所以 是原方程的解.
检验:当 时,左边= =右边,
5.一个两位数个位上的数是1,十位上的数是x,把1与x对调,新两位数比原两位数小18,试列出关于x的方程,并解这个方程.
解:依题意,得 10x+1-(10+x) = 18,
9x-9 = 18,
9x = 27,
x = 3.
1.等式的性质1 等式两边加(或减)__________ (或式子),结果仍相等. 字母表示成______________________________.
2.等式的性质2 等式两边乘__________,或除以 同一个不为0的数,结果仍_______.
字母表示成_________________________________.
同一个数
同一个数
相等
课堂小结
3.1 从算式到方程
第2课时 等式的性质
学习目标
1.理解等式的两条性质
2.会利用等式的性质解简单的一元一次方程
3.培养观察、分析、概括及逻辑思维能力,形成独立思考与合作交流的良好学习习惯
1.像m+n=n+m,x+2x=3x,3×3+1=5×2,3x+1=5y 这样的式子,都是等式;
2.用等号表示相等关系的式子,叫做等式;
3.通常可以用a=b表示一般的等式.
学习回顾
等号
把一个等式看作一个天平,等号两边的式子看作天平两边的物体, 则等式成立可以看作是天平两边保持平衡.
新课导入
(1)3x-5=22;
(2)0.28-0.13y=0.27y+1.
用估算的方法可以求出简单的一元一次方程解.
你能用估算的方法求出下列方程的解吗?
用估算的方法解比较复杂的方程是困难的.
因此,我们要讨论怎样解方程?
问题1:观察下面的操作过程,你能发现什么规律?
+
-
如果在平衡天平的两边,都加(或减)同样的量,天平还保持平衡.
等式的性质1:
等式两边加(或减)同一个数(或式子), 结果仍相等.
如果a=b,那么a±c=b±c.
问题2:观察下面的操作过程,你能发现什么规律?
×2
×3
天平在 增加 相同倍数重量的物体时,天平仍保持平衡.
÷2
÷3
减少
等式的性质2
等式两边乘同一个数,或除以同一个不等于0的数,结果仍相等.
如果a=b,那么ac=bc;
如果a=b(c ≠ 0),那么
(1)在运用等式的性质时,要特别注意关键词
“两边”和“同一个”,特别是“同一个”.
运用等式的性质时应注意:
(2)在运用等式的性质1时,两边加(或减)的可以是“同一个数”,也可以是“同一个式子”.
(3)在运用等式的性质2时,除以的同一个数不能为“0”,并且不能随便乘或除以“同一个式子”.
例:利用等式的性质解下列方程.
(1)x+7=26;
解:两边减7,得
x = 19.
于是
x+7-7=26-7.
(2)-5x=20;
解:两边除以-5,得
于是
x = -4.
解以x为未知数的方程,就是把方程逐步转化为x=a(a为常数)的形式,等式的性质是转化的重要依据.
解:两边加 5,得
化简,得
两边乘-3,得
x = -27.
(3) ;
将x = -27代入方程的左边,
得
方程的左右两边相等,
所以 x = -27是方程
的解.
检验:
随堂练习
1.下列变形符合等式性质的是( )
A.如果2x-3=7,那么2x=7-3
B.如果3x-2=1,那么3x=1-2
C.如果-2x=5,那么x=5+2
D
2. 下列说法错误的是( )
A.若x=3,则3=x.
B.若x=y,y=z,则x=z.
C.若ab=1,则a= .
D.若2+a=b-3, 则4+2a=2b -3.
D
-6
3. 如果mx=my,那么下列等式中不一定成立的是( )
A.mx+1=my+1
B.mx-3=my-3
C.-mx=-my
D.x=y
D
前提:m≠0
4. 利用等式的性质解下列方程并检验.
(1)5- x=-5;
解:两边减5,得
5- x-5=-5-5.
化简,得
x = -10.
两边除以 ,得
x = 50.
检验:当x = 50时,左边=5- ×50 =-5 =右边.
所以 x=50是原方程的解.
(2) .
解:两边加 ,得 .
化简,得 .
两边除以 ,得 .
所以 是原方程的解.
检验:当 时,左边= =右边,
5.一个两位数个位上的数是1,十位上的数是x,把1与x对调,新两位数比原两位数小18,试列出关于x的方程,并解这个方程.
解:依题意,得 10x+1-(10+x) = 18,
9x-9 = 18,
9x = 27,
x = 3.
1.等式的性质1 等式两边加(或减)__________ (或式子),结果仍相等. 字母表示成______________________________.
2.等式的性质2 等式两边乘__________,或除以 同一个不为0的数,结果仍_______.
字母表示成_________________________________.
同一个数
同一个数
相等
课堂小结
