圆的垂径定理[上学期]

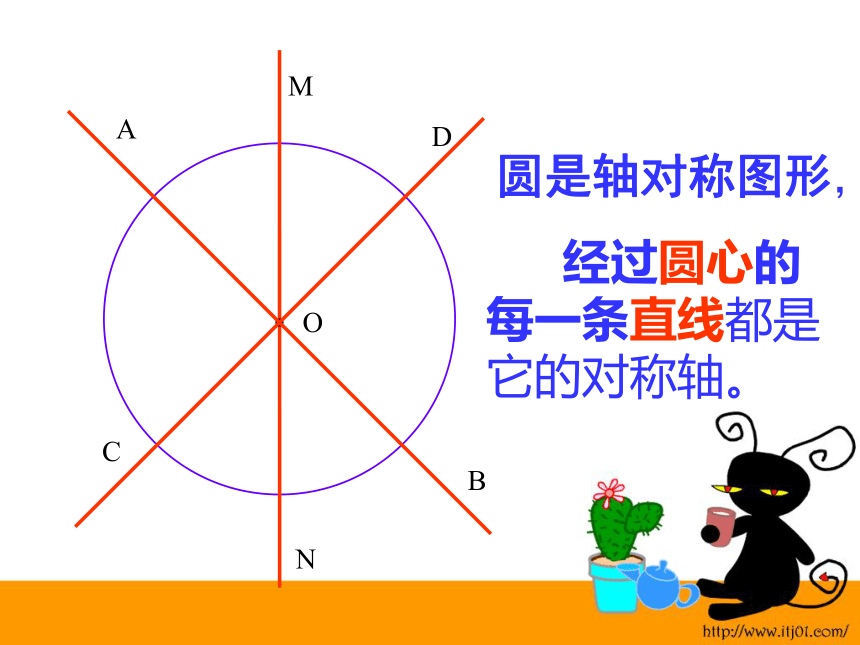
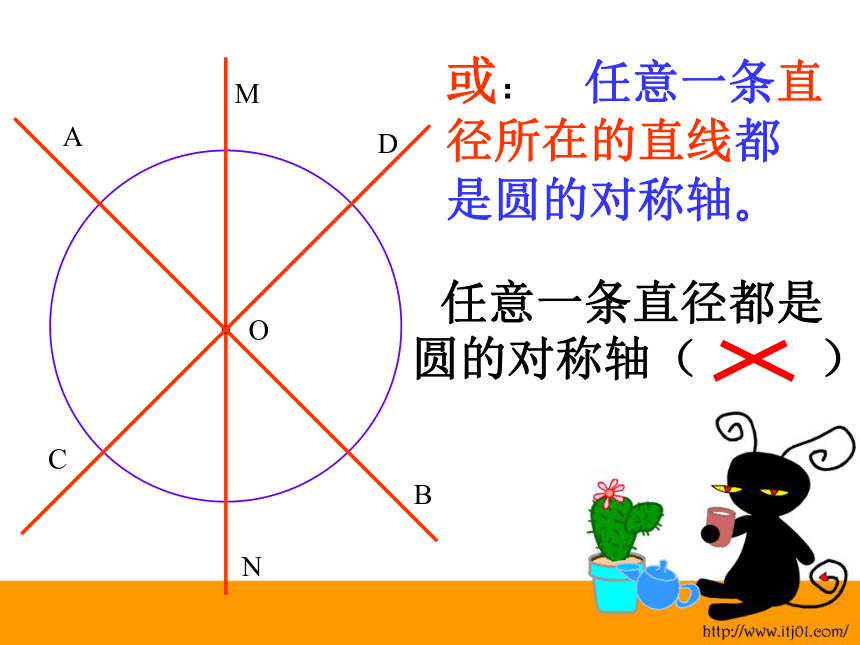
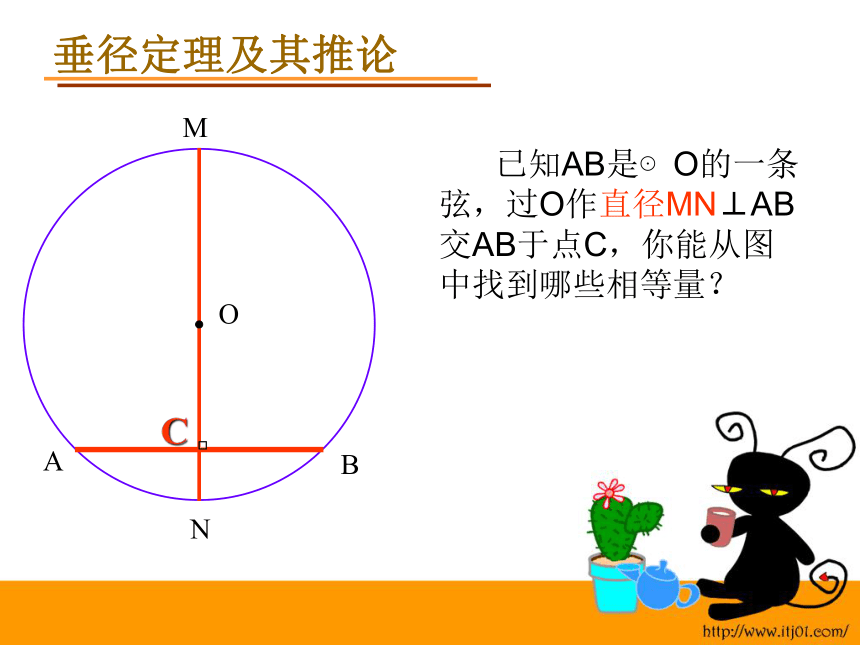
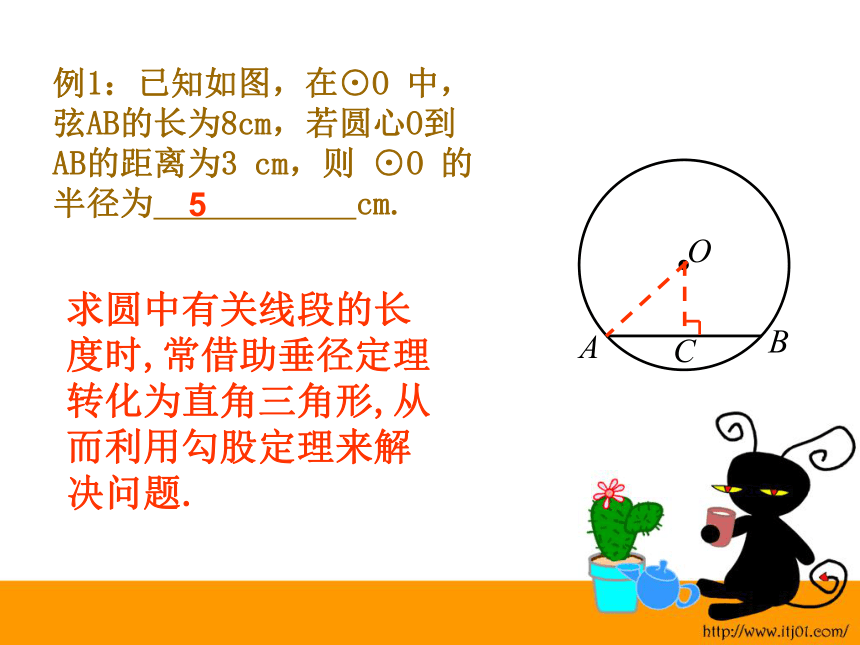
课件16张PPT。制作：厦门六中 郭祯圆的轴对称性及垂径定理圆的轴对称性 圆是中心对称图形,也是旋转对称图形。旋转角度可以是任意度数。 那么，圆是轴对称图形吗？如果是，它的对称轴是什么，有几条？OACBNMD圆是轴对称图形， 经过圆心的每一条直线都是它的对称轴。OACBNMD或： 任意一条直径所在的直线都是圆的对称轴。 任意一条直径都是圆的对称轴（ ）垂径定理及其推论MOACBN 已知AB是⊙O的一条弦，过O作直径MN⊥AB交AB于点C，你能从图中找到哪些相等量？垂径定理及其推论在⊙O中，如果CD是直径,CD⊥AB于E，那么：AE=BE（E是AB中点） 垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。例1：已知如图，在⊙O 中，弦AB的长为8cm，若圆心O到AB的距离为3 cm，则 ⊙O 的半径为 cm.
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 5Ｂ垂径定理的几种变型图(1)(2)(3)垂径：实际上是过圆心的线即可，一般作半径和弦心距两种。1、如何求弦心距：
如图，在⊙O中，半径为5cm，弦AB长为8cm，
求①圆心到弦的距离（弦心距）为 ，②弦AB的中点到劣弧AB的中点的距离过O作OE⊥AB于E，连接OA、OB，则OE为所求延长OE到D，交弧AB于D，则DE为所求问题归结到在以半径为斜边，半弦、弦心距为直角边的直角三角形中解答。垂径定理的应用1、同心圆O中，大圆的直径AB交小圆于点C、D，请问AC=BD吗？
2、如果把AB向下平移，弦AB仍然交小圆于点C、D，此时图中还有哪些相等的线段？为什么？12、在圆中研究有关弦的问题时，常过圆心作垂直于弦的垂线段，利用垂径定理来证明线段相等、弧相等,利用勾股定理列方程进行计算. 3. 已知⊙O的直径是50 cm，⊙O的两条平行弦AB=40 cm ，CD=48cm，求弦AB与CD之间的距离。 CD20152525247CDFEF有两解：15+7=22cm
15-7=8cm垂径定理及其推论1、按图填空，在⊙O中
(1) ∵ CD⊥AB于E, CD是直径
∴ ， ， ，

（2） ∵ AE=BE , CD是直径
∴ ， ， ，
（3） ∵ CD⊥AB于E, AE=BE
∴ ， ， ，
（4） ∵ CD是直径 , 弧AD=弧BD
∴ ， ， ，
（5） ∵ 弧AD=弧BD , 弧AC=弧BC
∴ ， ， ， 2、如图，AB是⊙O的直径，弦CD与AB相交于点E，若 ，则CE=DE。（只需填一个条件） 3、如图，CD是⊙O的直径，AB是弦，CD⊥AB，垂足为M，则 可得出AM=BM，弧AC=弧BC，请你按所绘图形在写出另两个结论弓形的概念及弓形高1、弓形：圆中一条弦及弦所对弧所组成的图形2、弓形高：弧中点到弦的距离例1：1300年前，我国隋朝建造的赵州石拱桥的桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4米，拱高（弧的中点到弦的距离，也叫弓形高）为7.2米，求桥 拱的半径（精确到0.1米）例2：在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=600mm，求油的最大深度。