6.1 平方根 课件(共20张PPT) 2022-2023学年人教版七年级数学下册
文档属性
| 名称 | 6.1 平方根 课件(共20张PPT) 2022-2023学年人教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
平方根与算术平方根
课堂目标
1、理解开方与乘方互为逆运算,了解算术平方根、平方根的概念,会用符号表示平方根、算术平方根。
2、了解平方根与算术平方根的区别与联系。
3、认识算术平方根的非负性和平方根性质,并解决一些计算问题。
知识讲解
算术平方根:
一般的,如果一个正数X的平方等于a,即x2=a,那么这个正数x叫做a的算数平方根. a的算术平方根记作“ ”,读作“根号a”,其中a叫做被开方数.
规定:0的算术平方根是0.
注意: 具有双重非负性:①被开方数≥0;②结果≥0
平方根:一般地 ,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根或二次方根.非负数a的平方根记为“± ” ,读作“正负根号a”,其中a叫做被开方数.
注意:一个正数平方根的结果有两个,并且互为相反数。
常考题型:
算术平方根:
一、求一个数的算术平方根(双重开方)
二、双重非负性
平方根:
一、求一个数的平方根(双重开方)
二、依据平方根求参数
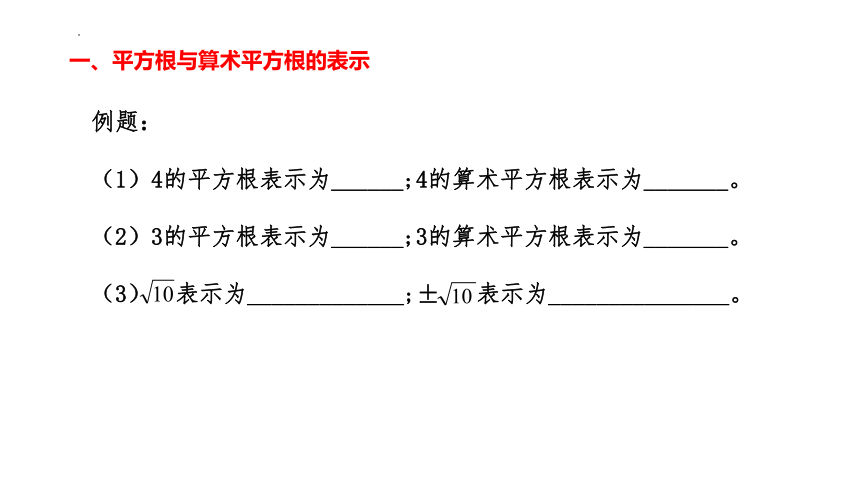
一、平方根与算术平方根的表示
例题:
(1)4的平方根表示为______;4的算术平方根表示为_______。
(2)3的平方根表示为______;3的算术平方根表示为_______。
(3) 表示为_____________;± 表示为_______________。
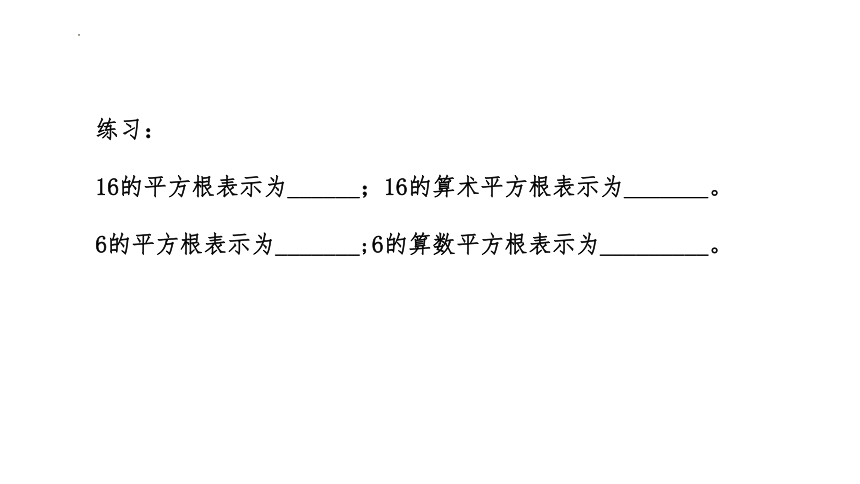
练习:
16的平方根表示为______;16的算术平方根表示为_______。
6的平方根表示为_______;6的算数平方根表示为_________。
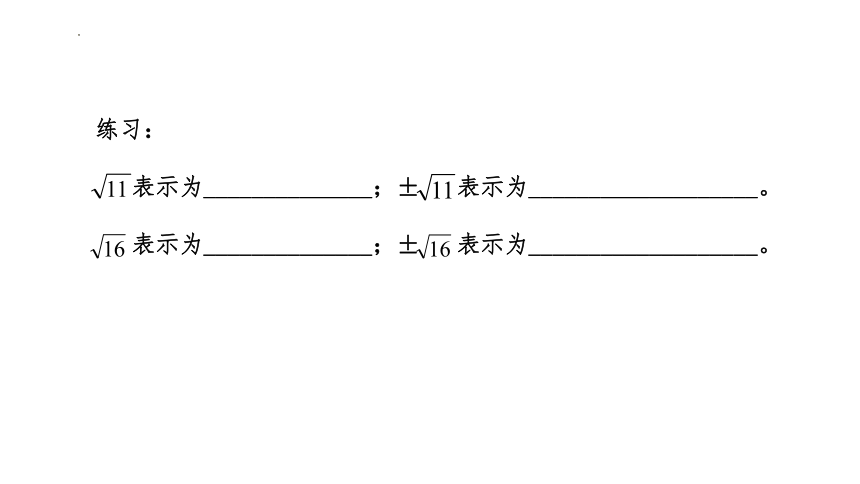
练习:
表示为______________;± 表示为___________________。
表示为______________;± 表示为___________________。
二、双重开方
例题:
的算术平方根是( )
A.2 B.4 C.±4 D.±2
练习:
的算术平方根是________.
练习:
的算术平方根的倒数是( )
A. B.4 C.2 D.
练习:
的平方根是( )
A.3 B.±3 C. D.±
练习:
的平方根是________.
三、非负性
例题:
已知 +(y 3)2=0,求3x y的值.
练习:
如果 与 互为相反数,那么
x2+y=________.
练习:
已知 +|3x+2y 15|=0,则 的算术平方根为________.
四、依据性质求参数
例题:
已知一个数a的平方根分别是x+9和x 3,分别求出a与x的值.
练习:
一个正数的平方根分别是 x+1 和x 5,则x=________.
练习:
一个正数的两个平方根分别是 2a 1 与 a+2,则a的值为( )
A. 1 B.1 C.2 D. 2
练习:
一个正数的x的平方根是 2a 3 与5 a,求a和x的值.
总结
算术平方根 平方根
区别 定义不同 一般地,如果一个正数x的平方等于a,即x =a,那么这个正数x叫做a的算术平方根 如果一个数的平方等于 ,这个数就叫做 的平方根或二次方根.
个数不同 一个正数的算术平方根只有一个 一个正数的平方根有两个,它们互为相反数
表示的方法不同 正数a的算术平方根记为 正数a的平方根记为±
结果不同 正数的算术平方根一定是正数 正数的平方根一正一负
联系 具有包含关系 平方根包含算术平方根,一个正数的平方根中的正的平方根就是这个正数的算术平方根.
存在条件相同 正数既有算术平方根又有平方根
平方根与算术平方根
课堂目标
1、理解开方与乘方互为逆运算,了解算术平方根、平方根的概念,会用符号表示平方根、算术平方根。
2、了解平方根与算术平方根的区别与联系。
3、认识算术平方根的非负性和平方根性质,并解决一些计算问题。
知识讲解
算术平方根:
一般的,如果一个正数X的平方等于a,即x2=a,那么这个正数x叫做a的算数平方根. a的算术平方根记作“ ”,读作“根号a”,其中a叫做被开方数.
规定:0的算术平方根是0.
注意: 具有双重非负性:①被开方数≥0;②结果≥0
平方根:一般地 ,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根或二次方根.非负数a的平方根记为“± ” ,读作“正负根号a”,其中a叫做被开方数.
注意:一个正数平方根的结果有两个,并且互为相反数。
常考题型:
算术平方根:
一、求一个数的算术平方根(双重开方)
二、双重非负性
平方根:
一、求一个数的平方根(双重开方)
二、依据平方根求参数
一、平方根与算术平方根的表示
例题:
(1)4的平方根表示为______;4的算术平方根表示为_______。
(2)3的平方根表示为______;3的算术平方根表示为_______。
(3) 表示为_____________;± 表示为_______________。
练习:
16的平方根表示为______;16的算术平方根表示为_______。
6的平方根表示为_______;6的算数平方根表示为_________。
练习:
表示为______________;± 表示为___________________。
表示为______________;± 表示为___________________。
二、双重开方
例题:
的算术平方根是( )
A.2 B.4 C.±4 D.±2
练习:
的算术平方根是________.
练习:
的算术平方根的倒数是( )
A. B.4 C.2 D.
练习:
的平方根是( )
A.3 B.±3 C. D.±
练习:
的平方根是________.
三、非负性
例题:
已知 +(y 3)2=0,求3x y的值.
练习:
如果 与 互为相反数,那么
x2+y=________.
练习:
已知 +|3x+2y 15|=0,则 的算术平方根为________.
四、依据性质求参数
例题:
已知一个数a的平方根分别是x+9和x 3,分别求出a与x的值.
练习:
一个正数的平方根分别是 x+1 和x 5,则x=________.
练习:
一个正数的两个平方根分别是 2a 1 与 a+2,则a的值为( )
A. 1 B.1 C.2 D. 2
练习:
一个正数的x的平方根是 2a 3 与5 a,求a和x的值.
总结
算术平方根 平方根
区别 定义不同 一般地,如果一个正数x的平方等于a,即x =a,那么这个正数x叫做a的算术平方根 如果一个数的平方等于 ,这个数就叫做 的平方根或二次方根.
个数不同 一个正数的算术平方根只有一个 一个正数的平方根有两个,它们互为相反数
表示的方法不同 正数a的算术平方根记为 正数a的平方根记为±
结果不同 正数的算术平方根一定是正数 正数的平方根一正一负
联系 具有包含关系 平方根包含算术平方根,一个正数的平方根中的正的平方根就是这个正数的算术平方根.
存在条件相同 正数既有算术平方根又有平方根
