5.3.1平行线的性质 课件 (共19张PPT)人教版七年级下册数学
文档属性
| 名称 | 5.3.1平行线的性质 课件 (共19张PPT)人教版七年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 518.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
平行线的性质
知识讲解
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
知识讲解
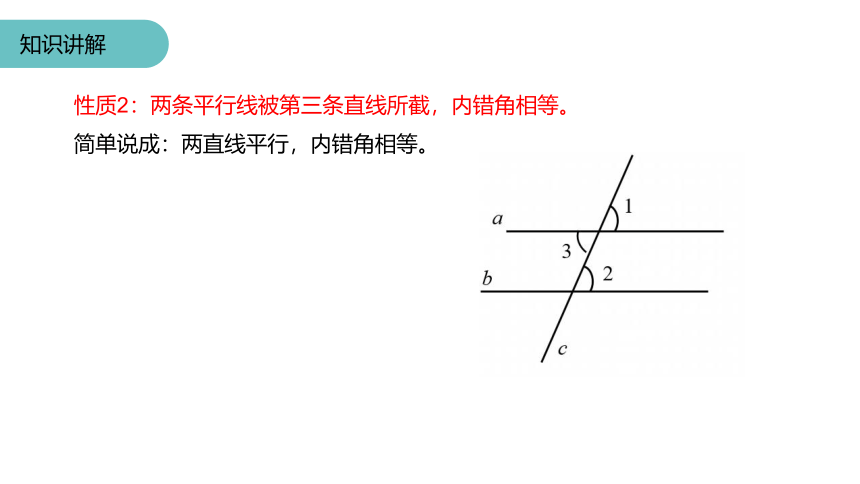
性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
知识讲解
性质3:两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
知识讲解
例题1
例题讲解
如图,若a//b,∠1=58°,则∠2的度数是( )
A.58°
B.112°
C.122°
D.142°
练习1
应用练习
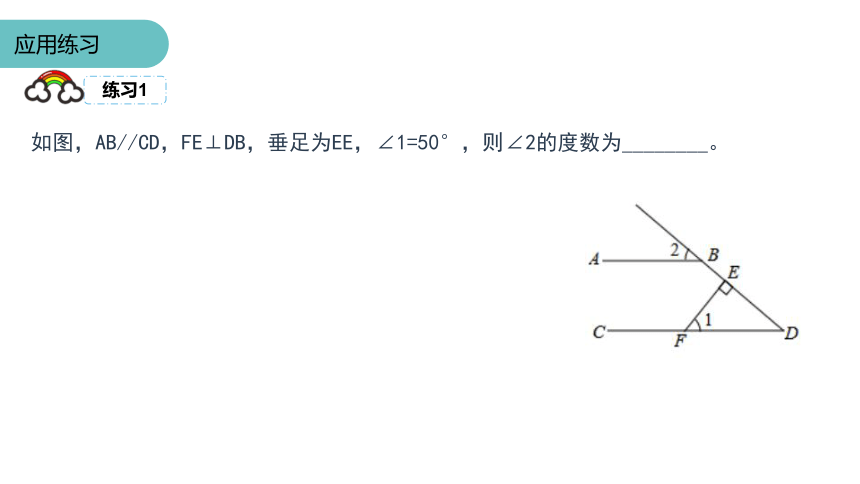
如图,AB//CD,FE⊥DB,垂足为EE,∠1=50°,则∠2的度数为________。
练习2
应用练习
如图,已知AB平行CD,且∠2=135°,则∠1的度数是( )
A.35°
B.45°
C.55°
D.65°
例题2
例题讲解
如图,BE//AF,点D是AB上一点,且DC⊥BE于点C,若∠A=35°,则∠ADC的度数( )
A.105°
B.115°
C.125°
D.135°
练习1
应用练习
如图,直线AB//CD,AG平分∠BAE,∠EFC=40°,则∠GAF的度数为( )
A.110°
B.115°
C.125°
D.130°
练习2
应用练习
如图,BC⊥AE于点C,CD//AB,∠ECD=50°,则∠B=( )
A.70°
B.60°
C.50°
D.40°
例题3
例题讲解
如图,直线//,若∠1=124°,∠2=88°,则∠3的度数( )
A.26°
B.36°
C.46°
D.56°
练习1
应用练习
如图所示,AB//CD,BE交CD于点E,射线BF平分∠ABE交CD于点F,若∠1=108°,
则∠BFE的度数为( )
A.36°
B.45°
C.41°
D.54°
A
B
C
D
E
F
1
)
练习2
应用练习
如图,AB//CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED=( )
A.55°
B.125°
C.135°
D.140°
例题4
例题讲解
如图,EF//AD,∠1=∠2,∠BAC=80°.求∠AGD。
解:∵EF//AD,
∴∠2=________。(________)
∵∠1=∠2,
∴∠1=∠3。(________)
∴AB//________。(________)
∴∠BAC+________=180° (________)
∵∠BAC=80°,
∴∠AGD=________。
练习1
应用练习
解: ∠A =∠D.理由:
∵ AB∥DE( )
∴∠A=_______( )
∵AC∥DF( )
∴∠D=______ ( )
∴∠A=∠D ( )
如图1,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
P
F
C
E
B
A
D
练习1
应用练习
如图2,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A+∠D=180°. 理由:
∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180°( )
∴∠A+∠D=180°( )
F
C
E
B
A
D
P
练习2
应用练习
如图,已知∠1+∠2=180°,∠3=∠B,试说明DE//BC,下面是部分推导过程,
请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4( )
∴∠2+∠4=180°(等量代换)
∴EH//AB( )
∴∠B=________( )
∵∠3=∠B(已知)
∴∠3=∠EHC( )
∴DE//BC( )
课堂大总结
平行线的性质:
①两直线平行,同位角相等;
②两直线平行,内错角相等;
③两直线平行,同旁内角互补。
平行线的性质
知识讲解
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
知识讲解
性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
知识讲解
性质3:两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
知识讲解
例题1
例题讲解
如图,若a//b,∠1=58°,则∠2的度数是( )
A.58°
B.112°
C.122°
D.142°
练习1
应用练习
如图,AB//CD,FE⊥DB,垂足为EE,∠1=50°,则∠2的度数为________。
练习2
应用练习
如图,已知AB平行CD,且∠2=135°,则∠1的度数是( )
A.35°
B.45°
C.55°
D.65°
例题2
例题讲解
如图,BE//AF,点D是AB上一点,且DC⊥BE于点C,若∠A=35°,则∠ADC的度数( )
A.105°
B.115°
C.125°
D.135°
练习1
应用练习
如图,直线AB//CD,AG平分∠BAE,∠EFC=40°,则∠GAF的度数为( )
A.110°
B.115°
C.125°
D.130°
练习2
应用练习
如图,BC⊥AE于点C,CD//AB,∠ECD=50°,则∠B=( )
A.70°
B.60°
C.50°
D.40°
例题3
例题讲解
如图,直线//,若∠1=124°,∠2=88°,则∠3的度数( )
A.26°
B.36°
C.46°
D.56°
练习1
应用练习
如图所示,AB//CD,BE交CD于点E,射线BF平分∠ABE交CD于点F,若∠1=108°,
则∠BFE的度数为( )
A.36°
B.45°
C.41°
D.54°
A
B
C
D
E
F
1
)
练习2
应用练习
如图,AB//CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED=( )
A.55°
B.125°
C.135°
D.140°
例题4
例题讲解
如图,EF//AD,∠1=∠2,∠BAC=80°.求∠AGD。
解:∵EF//AD,
∴∠2=________。(________)
∵∠1=∠2,
∴∠1=∠3。(________)
∴AB//________。(________)
∴∠BAC+________=180° (________)
∵∠BAC=80°,
∴∠AGD=________。
练习1
应用练习
解: ∠A =∠D.理由:
∵ AB∥DE( )
∴∠A=_______( )
∵AC∥DF( )
∴∠D=______ ( )
∴∠A=∠D ( )
如图1,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
P
F
C
E
B
A
D
练习1
应用练习
如图2,若AB∥DE , AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A+∠D=180°. 理由:
∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180°( )
∴∠A+∠D=180°( )
F
C
E
B
A
D
P
练习2
应用练习
如图,已知∠1+∠2=180°,∠3=∠B,试说明DE//BC,下面是部分推导过程,
请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4( )
∴∠2+∠4=180°(等量代换)
∴EH//AB( )
∴∠B=________( )
∵∠3=∠B(已知)
∴∠3=∠EHC( )
∴DE//BC( )
课堂大总结
平行线的性质:
①两直线平行,同位角相等;
②两直线平行,内错角相等;
③两直线平行,同旁内角互补。
