3.1.3函数的概念及其表示(第三课时) 课件(共21张PPT)
文档属性
| 名称 | 3.1.3函数的概念及其表示(第三课时) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 546.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 18:25:59 | ||
图片预览







文档简介
(共21张PPT)
第三章 函数的概念与性质
3.1.3 函数三要素
高中数学/人教A版/必修一
前面我们学习过函数的三个要素,即对应关系、定义域、值域.
函数是对现实世界变量之间关系的刻画;现实中变量的关系纷繁复杂,从而函数关系类型多样,结构有简有繁.
例1.根据下列条件,求f(x)的解析式.
(1)f [f(x)]=4x-3, 其中f(x)为一次函数;
(2) f(x+)= x2 + (3)f(x)+2f(-x)=x2+2x
(1)解:由题意,设 f(x)=ax+b(a≠0).
则 f [f(x)]=a(ax+b)+b=4x-3, 即a2=4,且ab+b=-3;
解得:a=2,b=-1; 或 a=-2,b=3
所以 f(x)=2x-1; 或 f(x)=-2x+3
1
求函数解析式
总结:已知函数类型,可用待定系数法.
例1.根据下列条件,求f(x)的解析式.
(1)f [f(x)]=4x-3, 其中f(x)为一次函数;
(2) f(x+)= x2 + (3)f(x)+2f(-x)=x2+2x
(2)解:因为f(x+)= x2 + =(x+)2-2 , 所以 f(x)=x2-2
又因为x+≥2 或x+≤-2
所以f(x)=x2-2 (x≥2 或 x≤-2 )
1
求函数解析式
总结:已知f [g(x)]表达式,可用配凑法求f(x)解析式;
要注意自变量的范围.
例1.根据下列条件,求f(x)的解析式.
(1)f [f(x)]=4x-3, 其中f(x)为一次函数;
(2) f(x+)= x2 + (3)f(x)+2f(-x)=x2+2x
(3)解:已知f(x)+2f(-x)=x2+2x
将其中的x换成-x, 得到 f(-x)+2f(x)=x2-2x
联立以上两式并消去f(-x),得f(x)=x2-2x
1
求函数解析式
总结:已知一个关于f (x)和f(-x)的方程,再构造一个对偶
式,然后消元即可.
练一练
根据下列条件,求f(x)的解析式.
(1)3f(x+1)-f(x)=2x+9, 其中f(x)为一次函数;
(2) f(x+1)= x2 +4x+1
(3)2f()+f(x)=x
答案:(1)f(x)=x+3; (2) f(x)= x2 +2x-2
(3)f(x)=-
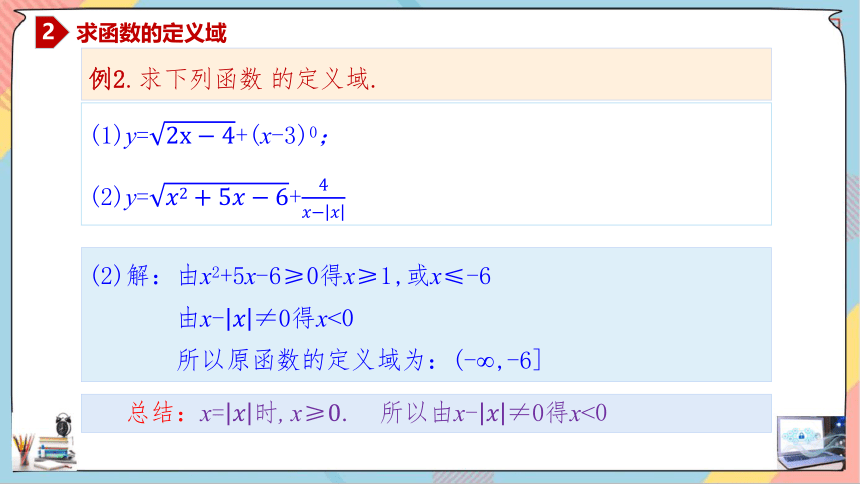
例2.求下列函数 的定义域.
(1)y=+(x-3)0;
(2)y=+
(1)解:由2x-4≥0得x≥2
由x-3≠0得x≠3
所以原函数的定义域为:[2,3)∪(3,+∞)
2
求函数的定义域
总结:开偶次方时,被开方数非负;
等式a0=1中,底数a≠0.
例2.求下列函数 的定义域.
(1)y=+(x-3)0;
(2)y=+
(2)解:由x2+5x-6≥0得x≥1,或x≤-6
由x-≠0得x<0
所以原函数的定义域为:(-∞,-6]
2
求函数的定义域
总结:x=, x≥0. 所以由x-≠0得x<0
练一练
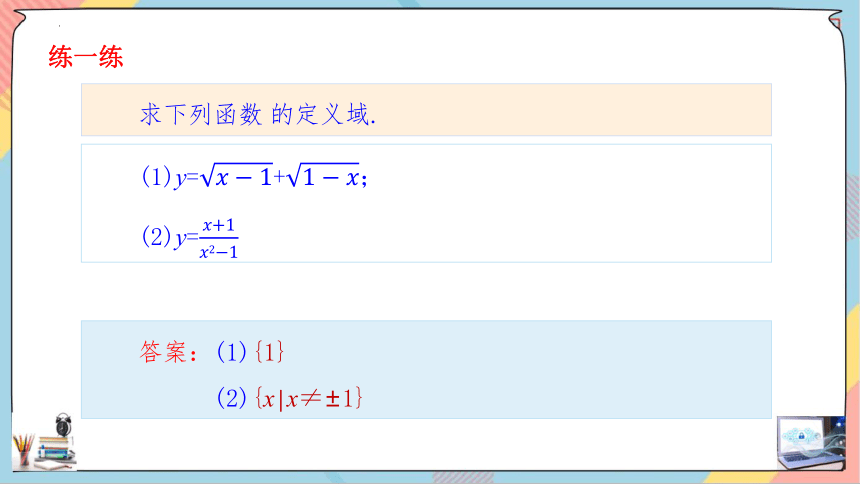
求下列函数 的定义域.
(1)y=+;
(2)y=
答案:(1){1}
(2){x│x≠±1}
例3.(1)已知f(x)的定义域为[-1,5],求f(2x-1)的定义域;
(2)已知f(2x-1)的定义域为[-1,5],求f(x)的定义域.
解:(1)由-1≤2x-1≤5 得 0≤x≤3;
即f(2x-1)的定义域为[0,3]
(2)由-1≤x≤5 得 -3≤2x-1≤9;
即f(x)的定义域为[-3,9]
2
求函数的定义域
总结:(1)已知f (x)的定义域为D,则f(g(x))中的g(x)∈D;
(2)已知f (g(x))的定义域为D,则
由x∈D推出g(x)∈E;得f(x)的定义域为E .
练一练
1.若f (x)的定义域为[0 , 3],则f (x-1)的定义域为 ;
2.若f (x-1)的定义域为[0 , 3],则f (x)的定义域为 .
答案:1. [1 , 4]
2. [-1 , 2]
例4.求下列函数的值域:
3
求函数的值域
(1)解:令t=,则t≥0, 且x=t2+1
所以 y=t2+2t+1=(t+1)2; 由于t≥0,
结合函数图象知,y≥1, 即值域为[1, +∞)
总结:通过换元,化归为二次函数在区间上的值域问题 .
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
例4.求下列函数的值域:
3
求函数的值域
(2)解: y===5+;
由于≠0,所以y≠5, 即值域为{y│y≠5}
总结:分式结构可先分离常数,再借助于反比例函数图象,
求得值域.
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
例4.求下列函数的值域:
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
3
求函数的值域
(3)解: y==;
因为≥3,所以0总结:高次式可通过配方或换元化归为二次式,再借助于
反比例函数图象,求得值域.
例4.求下列函数的值域:
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
3
求函数的值域
总结:分离常数后,要先求反比例型函数在指定区间上的
值域,需借助于反比例函数图象.
(4)解: y===5+;
由于x>2,所以∈(0,9), 即值域为(5, 14)
练一练
求下列函数的值域:
(1)y=x+; (2)y= .
答案:(1). [ , +∞)
(2). {y│y≠1}
课堂小结
一、本节课学习的新知识
由复合函数求原函数
复合函数的定义域
组合函数的值域
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学运算
三、本节课训练的数学思想方法
函数思想
课堂小结
数形结合
换元思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
给授课教师的建议:
1. 素养篇与思维篇中的问题,建议以学生分析为主,由
学生思考、探究、讨论,得出解决方案,教师适时点
拨即可;
2. 原PPT上的“分析”文本框内容,仅供教师参考,上
课前建议删除,使问题解决的过程得以原生态呈现.
(本页可以删了!)
第三章 函数的概念与性质
3.1.3 函数三要素
高中数学/人教A版/必修一
前面我们学习过函数的三个要素,即对应关系、定义域、值域.
函数是对现实世界变量之间关系的刻画;现实中变量的关系纷繁复杂,从而函数关系类型多样,结构有简有繁.
例1.根据下列条件,求f(x)的解析式.
(1)f [f(x)]=4x-3, 其中f(x)为一次函数;
(2) f(x+)= x2 + (3)f(x)+2f(-x)=x2+2x
(1)解:由题意,设 f(x)=ax+b(a≠0).
则 f [f(x)]=a(ax+b)+b=4x-3, 即a2=4,且ab+b=-3;
解得:a=2,b=-1; 或 a=-2,b=3
所以 f(x)=2x-1; 或 f(x)=-2x+3
1
求函数解析式
总结:已知函数类型,可用待定系数法.
例1.根据下列条件,求f(x)的解析式.
(1)f [f(x)]=4x-3, 其中f(x)为一次函数;
(2) f(x+)= x2 + (3)f(x)+2f(-x)=x2+2x
(2)解:因为f(x+)= x2 + =(x+)2-2 , 所以 f(x)=x2-2
又因为x+≥2 或x+≤-2
所以f(x)=x2-2 (x≥2 或 x≤-2 )
1
求函数解析式
总结:已知f [g(x)]表达式,可用配凑法求f(x)解析式;
要注意自变量的范围.
例1.根据下列条件,求f(x)的解析式.
(1)f [f(x)]=4x-3, 其中f(x)为一次函数;
(2) f(x+)= x2 + (3)f(x)+2f(-x)=x2+2x
(3)解:已知f(x)+2f(-x)=x2+2x
将其中的x换成-x, 得到 f(-x)+2f(x)=x2-2x
联立以上两式并消去f(-x),得f(x)=x2-2x
1
求函数解析式
总结:已知一个关于f (x)和f(-x)的方程,再构造一个对偶
式,然后消元即可.
练一练
根据下列条件,求f(x)的解析式.
(1)3f(x+1)-f(x)=2x+9, 其中f(x)为一次函数;
(2) f(x+1)= x2 +4x+1
(3)2f()+f(x)=x
答案:(1)f(x)=x+3; (2) f(x)= x2 +2x-2
(3)f(x)=-
例2.求下列函数 的定义域.
(1)y=+(x-3)0;
(2)y=+
(1)解:由2x-4≥0得x≥2
由x-3≠0得x≠3
所以原函数的定义域为:[2,3)∪(3,+∞)
2
求函数的定义域
总结:开偶次方时,被开方数非负;
等式a0=1中,底数a≠0.
例2.求下列函数 的定义域.
(1)y=+(x-3)0;
(2)y=+
(2)解:由x2+5x-6≥0得x≥1,或x≤-6
由x-≠0得x<0
所以原函数的定义域为:(-∞,-6]
2
求函数的定义域
总结:x=, x≥0. 所以由x-≠0得x<0
练一练
求下列函数 的定义域.
(1)y=+;
(2)y=
答案:(1){1}
(2){x│x≠±1}
例3.(1)已知f(x)的定义域为[-1,5],求f(2x-1)的定义域;
(2)已知f(2x-1)的定义域为[-1,5],求f(x)的定义域.
解:(1)由-1≤2x-1≤5 得 0≤x≤3;
即f(2x-1)的定义域为[0,3]
(2)由-1≤x≤5 得 -3≤2x-1≤9;
即f(x)的定义域为[-3,9]
2
求函数的定义域
总结:(1)已知f (x)的定义域为D,则f(g(x))中的g(x)∈D;
(2)已知f (g(x))的定义域为D,则
由x∈D推出g(x)∈E;得f(x)的定义域为E .
练一练
1.若f (x)的定义域为[0 , 3],则f (x-1)的定义域为 ;
2.若f (x-1)的定义域为[0 , 3],则f (x)的定义域为 .
答案:1. [1 , 4]
2. [-1 , 2]
例4.求下列函数的值域:
3
求函数的值域
(1)解:令t=,则t≥0, 且x=t2+1
所以 y=t2+2t+1=(t+1)2; 由于t≥0,
结合函数图象知,y≥1, 即值域为[1, +∞)
总结:通过换元,化归为二次函数在区间上的值域问题 .
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
例4.求下列函数的值域:
3
求函数的值域
(2)解: y===5+;
由于≠0,所以y≠5, 即值域为{y│y≠5}
总结:分式结构可先分离常数,再借助于反比例函数图象,
求得值域.
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
例4.求下列函数的值域:
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
3
求函数的值域
(3)解: y==;
因为≥3,所以0
反比例函数图象,求得值域.
例4.求下列函数的值域:
(1)y=x+; (2)y= ;
(3)y= (4)y= (x>2)
3
求函数的值域
总结:分离常数后,要先求反比例型函数在指定区间上的
值域,需借助于反比例函数图象.
(4)解: y===5+;
由于x>2,所以∈(0,9), 即值域为(5, 14)
练一练
求下列函数的值域:
(1)y=x+; (2)y= .
答案:(1). [ , +∞)
(2). {y│y≠1}
课堂小结
一、本节课学习的新知识
由复合函数求原函数
复合函数的定义域
组合函数的值域
二、本节课提升的核心素养
逻辑推理
数据分析
课堂小结
数学运算
三、本节课训练的数学思想方法
函数思想
课堂小结
数形结合
换元思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
给授课教师的建议:
1. 素养篇与思维篇中的问题,建议以学生分析为主,由
学生思考、探究、讨论,得出解决方案,教师适时点
拨即可;
2. 原PPT上的“分析”文本框内容,仅供教师参考,上
课前建议删除,使问题解决的过程得以原生态呈现.
(本页可以删了!)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
