3.1圆的对称性

课件20张PPT。3.1 圆的对称性1、在一个平面内，线段OP绕它固定的一个端点O旋转一周，则另一个端点P所形成的封闭曲线叫做圆。固定的端点O叫做圆心，线段OP叫做半径。以点O为圆心的圆，记作“⊙O”，读作“圆O”。一、圆的定义(旋转法定义)你还记得吗？二、圆的相关概念直径将圆分成两部分,每一部分都叫做半圆 (如半圆ABC).你还记得吗？圆的对称性1、圆是轴对称图形吗？2、如果是,它的对称轴是什么?
你能找到多少条对称轴？1、圆是轴对称图形2、圆的对称轴是每一条直径所在的直线,
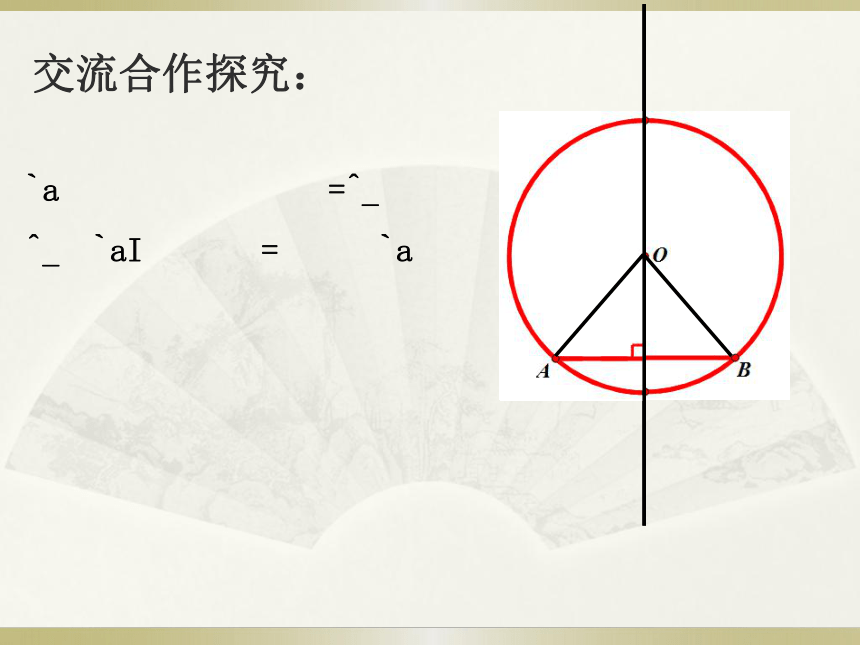
它有无数条对称轴.交流合作：DCD为⊙O 直径，作弦 AB，使AB⊥CD,若将⊙O 沿直径CD所
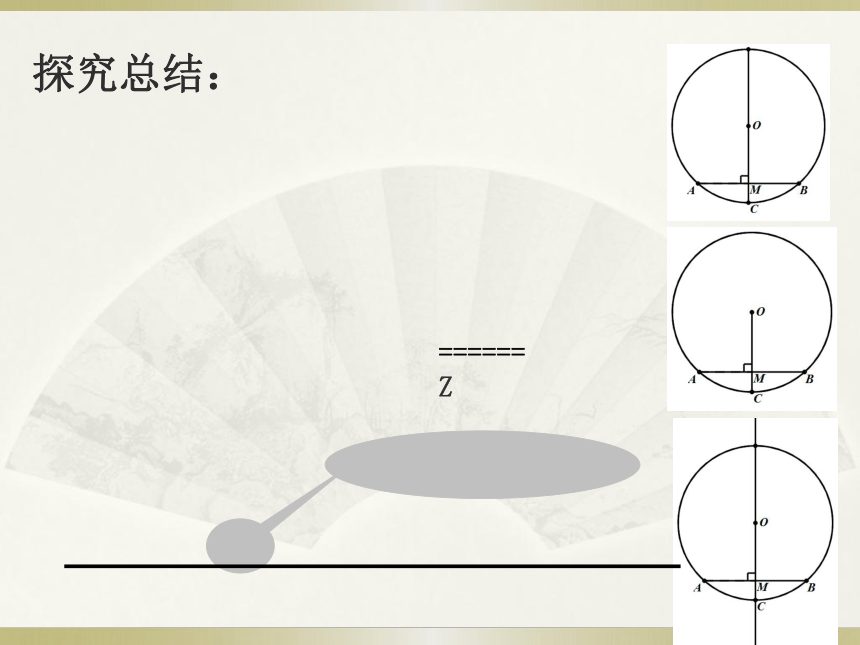
在的直线折叠，C交流合作探究：M探究总结：根据前面的分析，
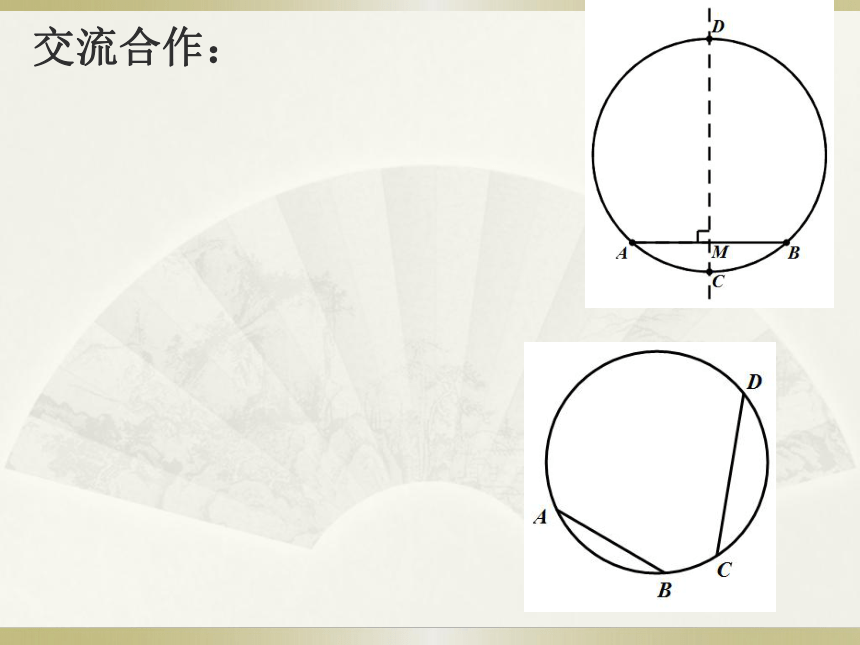
我们用数学语言表示一下条件和结论结论： AM=BM总结：垂径定理过圆心的直线或线段问题1：弦的垂直平分线一定过圆心吗？你还能得到什么结论？问题2:(如图)AB,CD为⊙O的弦，
你能确定圆心的位置吗？交流合作：1、已知：如图,⊙O 中,弦AB∥CD,AB＜CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有
图中相等的劣弧有:巩固练习： 2、如图，⊙O的半径为5cm，弦AB为6cm，求圆心O到弦AB的距离。巩固练习： 3、如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，四边形ADOE的形状？巩固练习： 4、已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。你认为AC和BD有什么关系？为什么？∟巩固练习： 5、如图，CD为圆O的直径，弦AB交CD于E，∠CEB=30°，DE=9㎝，CE=3㎝，求弦AB的长。典例应用 例1、1400多年前，我国隋代建造的赵州石拱桥的桥拱近似于圆弧形，它的跨度（弧所对的弦长）为37.02m，拱高（弧的中点到弦的
距离，也叫弓形的高）为7.23m。
求桥拱所在圆的半径。？？例2、如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？例2、如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？画一画1、如图,M为⊙O内的一点,利用尺规作一条弦AB,使点M是弦AB的中点吗？挑战自我 ① 垂径定理： ② 如何判断圆的圆心的位置 ③ 在解有关题目的时候，
常利用直角三角形的勾股定理！谈
收
获弦的垂直平分线必定经过圆心！经过圆心小结: 解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件。1、在直径是20cm的⊙O中， ∠AOB的度数是60°，那么弦AB的弦心距是　　　　　. 3、弓形的弦长为6cm，弓形的高为2cm，则这弓形所在的圆的半径为　　　　　　. 4、已知P为O内一点，且OP=2cm，如果O的半径是4cm，那么过P点的最短的弦等于 。2、在半径为30㎜的⊙O中，弦AB=36㎜，则O到AB的距离是= ，∠OAB的余弦值= 。24mm0.6在直径为650mm的圆柱形油槽内装入一些
油后，油面宽AB = 600mm，求油的最大深度. DC/C└└