2014高中数学生活中的变量关系同步课时训练 北师大版必修1
文档属性
| 名称 | 2014高中数学生活中的变量关系同步课时训练 北师大版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 213.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-22 15:27:42 | ||
图片预览



文档简介
2014高中数学生活中的变量关系同步课时训练 北师大版必修1
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.下列两个变量之间的关系不是函数关系的是( )
(A)大气层中的臭氧空洞的面积与时间(年份)
(B)圆的周长与半径
(C)正n边形的内角和与边数
(D)月份与年
2.下列变量间是函数关系的是( )
(A)匀速行驶的客车在2小时内行驶的路程
(B)某地蔬菜的价格与蔬菜的供应量的关系
(C)一只60瓦的白炽灯在七小时内的耗电量与时间t的关系
(D)生活质量与人的身体状况间的关系
3.(2012·成都高一检测)“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…….用S1,S2分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事情节相吻合的是( )
4.(2012·宁波高一检测)某商场对顾客实行购物优惠活动,规定一次性购物付款总额:
(1)如果不超过200元,则不予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠,某人单独购买A,B商品分别付款168元和423元,假设一次性购买A,B两件商品,则应付款是( )
(A)413.7元 (B)513.7元
(C)546.6元 (D)548.7元
二、填空题(每小题4分,共8分)
5.给出下列关系:
(1)人的年龄与他拥有的财富之间的关系.
(2)抛物线上的点与该点坐标之间的关系.
(3)橘子的产量与气候之间的关系.
其中不是函数关系的序号是:_________.
6.声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:
气温x/℃
0
5
10
15
20
音速y/(米/秒)
331
334
337
340
343
(1)此表反映的是变量_______________随_______________的变化.
(2)用x表示y的关系式为____________.
(3)气温为22℃时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地约相距______________米.
三、解答题(每小题8分,共16分)
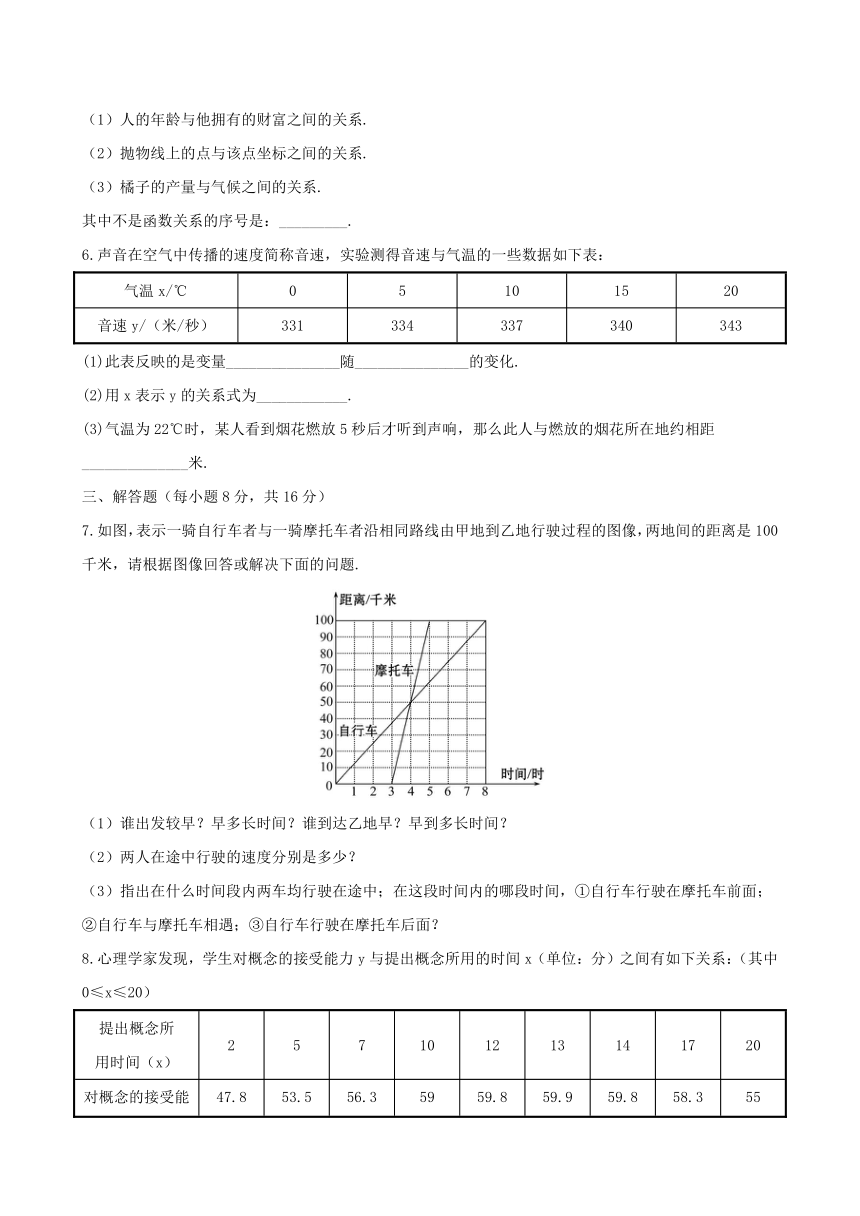
7.如图,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图像,两地间的距离是100千米,请根据图像回答或解决下面的问题.
(1)谁出发较早?早多长时间?谁到达乙地早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)指出在什么时间段内两车均行驶在途中;在这段时间内的哪段时间,①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面?
8.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系:(其中0≤x≤20)
提出概念所
用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强?
(4)从表格中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
【挑战能力】
(10分)如图所示为1984年到2008年的奥运会中,我国每届奥运会获得的金牌数.设年份为x(x∈{1984,1988,1992,1996,2000,2004,2008}),金牌数为y.
(1)试判断y是否为x的函数,x是否为y的函数;
(2)你能以此来推断2012年伦敦奥运会上中国有望突破60枚金牌吗?
答案解析
1.【解析】选D.因为月份对应的年份不确定,不符合函数的关系,故月份与年两个变量之间的关系不是函数关系.
2.【解析】选C.A是常量,B、D是依赖关系,C是确定的函数关系.
3.【解析】选D.由题意可知D中图像与故事吻合.
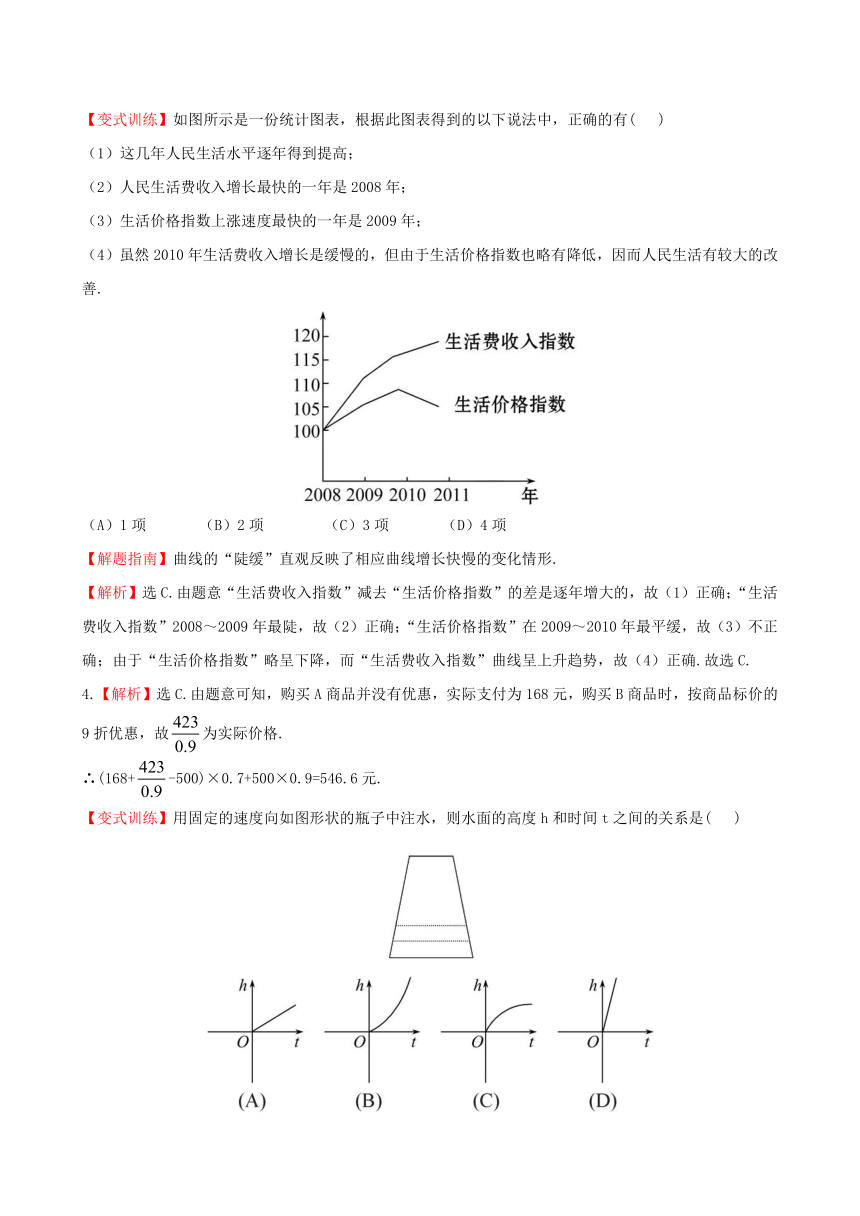
【变式训练】如图所示是一份统计图表,根据此图表得到的以下说法中,正确的有( )
(1)这几年人民生活水平逐年得到提高;
(2)人民生活费收入增长最快的一年是2008年;
(3)生活价格指数上涨速度最快的一年是2009年;
(4)虽然2010年生活费收入增长是缓慢的,但由于生活价格指数也略有降低,因而人民生活有较大的改善.
(A)1项 (B)2项 (C)3项 (D)4项
【解题指南】曲线的“陡缓”直观反映了相应曲线增长快慢的变化情形.
【解析】选C.由题意“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故(1)正确;“生活费收入指数”2008~2009年最陡,故(2)正确;“生活价格指数”在2009~2010年最平缓,故(3)不正确;由于“生活价格指数”略呈下降,而“生活费收入指数”曲线呈上升趋势,故(4)正确.故选C.
4.【解析】选C.由题意可知,购买A商品并没有优惠,实际支付为168元,购买B商品时,按商品标价的9折优惠,故为实际价格.
∴(168+-500)×0.7+500×0.9=546.6元.
【变式训练】用固定的速度向如图形状的瓶子中注水,则水面的高度h和时间t之间的关系是( )
【解题指南】解答本题的关键是首先分清谁是自变量,谁是因变量,然后结合已知条件及瓶子的形状确定因变量与自变量的变化规律.
【解析】选B.由题可知随着时间的增加水面的高度增加得越来越快,因此选B.
5.【解析】(1)人的年龄与他拥有的财富之间存在依赖关系,但不是函数关系;(3)橘子的产量与气候之间存在依赖关系,但不是函数关系;(2)是函数关系.
答案:(1)(3)
6. 【解析】(1)此表反映的是变量音速随气温的变化;
(2)由表中数据可知,气温每升高5℃,音速加快3米/秒,又过点(0,331),故所求函数关系式为y=x+331.
(3)由(2)可知气温为22℃时音速y=×22+331,
故此人与燃放的烟花所在地约相距为5×(×22+331)=66+1 655=1 721米.
答案:(1)音速 气温 (2)y=x+331 (3)1 721
【误区警示】本题在求解(3)时常因把音速y错误地理解成距离而出错.
7. 【解析】(1)自行车出发较早,早3个小时,摩托车到达乙地较早,早3个小时.
(2)自行车:12.5千米/时;摩托车:50千米/时.
(3)自行车出发3~5小时内,两车均行驶在途中.①当3<x<4时,自行车行驶在摩托车前面;②当x=4时,自行车与摩托车相遇;③当4<x<5时,自行车行驶在摩托车后面.(其中x为自行车出发后经过的时间)
8.【解题指南】(1)根据x,y表示的意义以及函数的概念即可判定;
(2)根据表格即可直接写出;
(3)学生的接受能力最强,即y的值最大,即可确定对应的x值;
(4)根据表格可以得到y的值在未超过13分钟时越来越大,超过13分钟时越来越小,即可得解.
【解析】(1)反映了提出概念所用的时间x和对概念接受能力y两个变量之间的关系;其中x是自变量,y是因变量.
(2)由题中表格可知,当提出概念所用时间为10分钟时,学生接受能力是59.
(3)提出概念所用的时间为13分钟时,学生的接受能力最强.
(4)当x在2分钟至13分钟的范围内,学生的接受能力逐步增强;当x在13分钟至20分钟的范围内,学生的接受能力逐步降低.
【挑战能力】
【解析】(1)由图知,获得的金牌数y随着年份x的变化而变化,对于每一个x的值,都有唯一确定的一个y与它相对应,所以获得的金牌数y是年份x的函数.
由图知,金牌数16对应了年份1992和1996,即对于每一个y的值,并非都有唯一确定的一个x与它相对应,所以年份x不是获得的金牌数y的函数.
(2)从1996年开始由于中国每届奥运会金牌数都呈递增趋势且每届平均增长量超过10枚,由此推断中国2012年在伦敦奥运会上有望突破60枚金牌.
3.2 古典概型(第四、五课时)
3.2.1 —3.2.2古典概型及随机数的产生
一、教学目标:
1、知识与技能:(1)正确理解古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等;
(2)掌握古典概型的概率计算公式:P(A)=
(3)了解随机数的概念;
(4)利用计算机产生随机数,并能直接统计出频数与频率。
2、过程与方法:(1)通过对现实生活中具体的概率问题的探究,感知应用数学解决问题的方法,体会数学知识与现实世界的联系,培养逻辑推理能力;(2)通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯。
3、情感态度与价值观:通过数学与探究活动,体会理论来源于实践并应用于实践的辩证唯物主义观点.
二、重点与难点:1、正确理解掌握古典概型及其概率公式;2、正确理解随机数的概念,并能应用计算机产生随机数.
三、学法与教学用具:1、与学生共同探讨,应用数学解决现实问题;2、通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯.
四、教学设想:
1、创设情境:(1)掷一枚质地均匀的硬币,结果只有2个,即“正面朝上”或“反面朝上”,它们都是随机事件。
(2)一个盒子中有10个完全相同的球,分别标以号码1,2,3,…,10,从中任取一球,只有10种不同的结果,即标号为1,2,3…,10。
师生共同探讨:根据上述情况,你能发现它们有什么共同特点?
2、基本概念:
(1)基本事件、古典概率模型、随机数、伪随机数的概念见课本P121~126;
(2)古典概型的概率计算公式:P(A)=.
3、例题分析:
课本例题略
例1 掷一颗骰子,观察掷出的点数,求掷得奇数点的概率。
分析:掷骰子有6个基本事件,具有有限性和等可能性,因此是古典概型。
解:这个试验的基本事件共有6个,即(出现1点)、(出现2点)……、(出现6点)
所以基本事件数n=6,
事件A=(掷得奇数点)=(出现1点,出现3点,出现5点),
其包含的基本事件数m=3
所以,P(A)====0.5
小结:利用古典概型的计算公式时应注意两点:
(1)所有的基本事件必须是互斥的;
(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏。
例2 从含有两件正品a1,a2和一件次品b1的三件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率。
解:每次取出一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件有6个,即(a1,a2)和,(a1,b2),(a2,a1),(a2,b1),(b1,a1),(b2,a2)。其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产用A表示“取出的两种中,恰好有一件次品”这一事件,则
A=[(a1,b1),(a2,b1),(b1,a1),(b1,a2)]
事件A由4个基本事件组成,因而,P(A)==
例3 现有一批产品共有10件,其中8件为正品,2件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2)如果从中一次取3件,求3件都是正品的概率.
分析:(1)为返回抽样;(2)为不返回抽样.
解:(1)有放回地抽取3次,按抽取顺序(x,y,z)记录结果,则x,y,z都有10种可能,所以试验结果有10×10×10=103种;设事件A为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此,P(A)= =0.512.
(2)解法1:可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(x,y,z),则x有10种可能,y有9种可能,z有8种可能,所以试验的所有结果为10×9×8=720种.设事件B为“3件都是正品”,则事件B包含的基本事件总数为8×7×6=336, 所以P(B)= ≈0.467.
解法2:可以看作不放回3次无顺序抽样,先按抽取顺序(x,y,z)记录结果,则x有10种可能,y有9种可能,z有8种可能,但(x,y,z),(x,z,y),(y,x,z),(y,z,x),(z,x,y),(z,y,x),是相同的,所以试验的所有结果有10×9×8÷6=120,按同样的方法,事件B包含的基本事件个数为8×7×6÷6=56,因此P(B)= ≈0.467.
小结:关于不放回抽样,计算基本事件个数时,既可以看作是有顺序的,也可以看作是无顺序的,其结果是一样的,但不论选择哪一种方式,观察的角度必须一致,否则会导致错误.
例4 利用计算器产生10个1~100之间的取整数值的随机数。
解:具体操作如下:键入
反复操作10次即可得之
小结:利用计算器产生随机数,可以做随机模拟试验,在日常生活中,有着广泛的应用。
例5 某篮球爱好者,做投篮练习,假设其每次投篮命中的概率是40%,那么在连续三次投篮中,恰有两次投中的概率是多少?
分析:其投篮的可能结果有有限个,但是每个结果的出现不是等可能的,所以不能用古典概型的概率公式计算,我们用计算机或计算器做模拟试验可以模拟投篮命中的概率为40%。
解:我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以生产0到9之间的取整数值的随机数。
我们用1,2,3,4表示投中,用5,6,7,8,9,0表示未投中,这样可以体现投中的概率是40%。因为是投篮三次,所以每三个随机数作为一组。
例如:产生20组随机数:
812,932,569,683,271,989,730,537,925,
907,113,966,191,431,257,393,027,556.
这就相当于做了20次试验,在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两次投中,它们分别是812,932,271,191,393,即共有5个数,我们得到了三次投篮中恰有两次投中的概率近似为=25%。
小结:(1)利用计算机或计算器做随机模拟试验,可以解决非古典概型的概率的求解问题。
(2)对于上述试验,如果亲手做大量重复试验的话,花费的时间太多,因此利用计算机或计算器做随机模拟试验可以大大节省时间。
(3)随机函数RANDBETWEEN(a,b)产生从整数a到整数b的取整数值的随机数。
例6 你还知道哪些产生随机数的函数?请列举出来。
解:(1)每次按SHIFT RNA# 键都会产生一个0~1之间的随机数,而且出现0~1内任何一个数的可能性是相同的。
(2)还可以使用计算机软件来产生随机数,如Scilab中产生随机数的方法。Scilab中用rand()函数来产生0~1之间的随机数,每周用一次rand()函数,就产生一个随机数,如果要产生a~b之间的随机数,可以使用变换rand()*(b-a)+a得到.
4、课堂小结:本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利用公式P(A)=
(3)随机数量具有广泛的应用,可以帮助我们安排和模拟一些试验,这样可以代替我们自己做大量重复试验,比如现在很多城市的重要考试采用产生随机数的方法把考生分配到各个考场中。
5、自我评价与课堂练习:
1.在40根纤维中,有12根的长度超过30mm,从中任取一根,取到长度超过30mm的纤维的概率是( )
A. B. C. D.以上都不对
2.盒中有10个铁钉,其中8个是合格的,2个是不合格的,从中任取一个恰为合格铁钉的概率是
A. B. C. D.
3.在大小相同的5个球中,2个是红球,3个是白球,若从中任取2个,则所取的2个球中至少有一个红球的概率是 。
4.抛掷2颗质地均匀的骰子,求点数和为8的概率。
5.利用计算器生产10个1到20之间的取整数值的随机数。
6.用0表示反面朝上,1表正面朝上,请用计算器做模拟掷硬币试验。
6、评价标准:
1.B[提示:在40根纤维中,有12根的长度超过30mm,即基本事件总数为40,且它们是等可能发生的,所求事件包含12个基本事件,故所求事件的概率为,因此选B.]
2.C[提示:(方法1)从盒中任取一个铁钉包含基本事件总数为10,其中抽到合格铁订(记为事件A)包含8个基本事件,所以,所求概率为P(A)==.(方法2)本题还可以用对立事件的概率公式求解,因为从盒中任取一个铁钉,取到合格品(记为事件A)与取到不合格品(记为事件B)恰为对立事件,因此,P(A)=1-P(B)=1-=.]
3.[提示;记大小相同的5个球分别为红1,红2,白1,白2,白3,则基本事件为:(红1,红2),(红1,白1),(红1,白2)(红1,白3),(红2,白3),共10个,其中至少有一个红球的事件包括7个基本事件,所以,所求事件的概率为.本题还可以利用“对立事件的概率和为1”来求解,对于求“至多”“至少”等事件的概率头问题,常采用间接法,即求其对立事件的概率P(A),然后利用P(A)1-P(A)求解]。
4.解:在抛掷2颗骰子的试验中,每颗骰子均可出现1点,2点,…,6点6种不同的结果,我们把两颗骰子标上记号1,2以便区分,由于1号骰子的一个结果,因此同时掷两颗骰子的结果共有6×6=36种,在上面的所有结果中,向上的点数之和为8的结果有(2,6),(3,5),(4,4),(5,3),(6,2)5种,所以,所求事件的概率为.
5.解:具体操作如下
键入
反复按 键10次即可得到。
6.解:具体操作如下:
键入
7、作业:根据情况安排
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.下列两个变量之间的关系不是函数关系的是( )
(A)大气层中的臭氧空洞的面积与时间(年份)
(B)圆的周长与半径
(C)正n边形的内角和与边数
(D)月份与年
2.下列变量间是函数关系的是( )
(A)匀速行驶的客车在2小时内行驶的路程
(B)某地蔬菜的价格与蔬菜的供应量的关系
(C)一只60瓦的白炽灯在七小时内的耗电量与时间t的关系
(D)生活质量与人的身体状况间的关系
3.(2012·成都高一检测)“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…….用S1,S2分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事情节相吻合的是( )
4.(2012·宁波高一检测)某商场对顾客实行购物优惠活动,规定一次性购物付款总额:
(1)如果不超过200元,则不予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠,某人单独购买A,B商品分别付款168元和423元,假设一次性购买A,B两件商品,则应付款是( )
(A)413.7元 (B)513.7元
(C)546.6元 (D)548.7元
二、填空题(每小题4分,共8分)
5.给出下列关系:
(1)人的年龄与他拥有的财富之间的关系.
(2)抛物线上的点与该点坐标之间的关系.
(3)橘子的产量与气候之间的关系.
其中不是函数关系的序号是:_________.
6.声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:
气温x/℃
0
5
10
15
20
音速y/(米/秒)
331
334
337
340
343
(1)此表反映的是变量_______________随_______________的变化.
(2)用x表示y的关系式为____________.
(3)气温为22℃时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地约相距______________米.
三、解答题(每小题8分,共16分)
7.如图,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图像,两地间的距离是100千米,请根据图像回答或解决下面的问题.
(1)谁出发较早?早多长时间?谁到达乙地早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)指出在什么时间段内两车均行驶在途中;在这段时间内的哪段时间,①自行车行驶在摩托车前面;②自行车与摩托车相遇;③自行车行驶在摩托车后面?
8.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间有如下关系:(其中0≤x≤20)
提出概念所
用时间(x)
2
5
7
10
12
13
14
17
20
对概念的接受能力(y)
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是10分钟时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念几分钟时,学生的接受能力最强?
(4)从表格中可知,当时间x在什么范围内,学生的接受能力逐步增强?当时间x在什么范围内,学生的接受能力逐步降低?
【挑战能力】
(10分)如图所示为1984年到2008年的奥运会中,我国每届奥运会获得的金牌数.设年份为x(x∈{1984,1988,1992,1996,2000,2004,2008}),金牌数为y.
(1)试判断y是否为x的函数,x是否为y的函数;
(2)你能以此来推断2012年伦敦奥运会上中国有望突破60枚金牌吗?
答案解析
1.【解析】选D.因为月份对应的年份不确定,不符合函数的关系,故月份与年两个变量之间的关系不是函数关系.
2.【解析】选C.A是常量,B、D是依赖关系,C是确定的函数关系.
3.【解析】选D.由题意可知D中图像与故事吻合.
【变式训练】如图所示是一份统计图表,根据此图表得到的以下说法中,正确的有( )
(1)这几年人民生活水平逐年得到提高;
(2)人民生活费收入增长最快的一年是2008年;
(3)生活价格指数上涨速度最快的一年是2009年;
(4)虽然2010年生活费收入增长是缓慢的,但由于生活价格指数也略有降低,因而人民生活有较大的改善.
(A)1项 (B)2项 (C)3项 (D)4项
【解题指南】曲线的“陡缓”直观反映了相应曲线增长快慢的变化情形.
【解析】选C.由题意“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故(1)正确;“生活费收入指数”2008~2009年最陡,故(2)正确;“生活价格指数”在2009~2010年最平缓,故(3)不正确;由于“生活价格指数”略呈下降,而“生活费收入指数”曲线呈上升趋势,故(4)正确.故选C.
4.【解析】选C.由题意可知,购买A商品并没有优惠,实际支付为168元,购买B商品时,按商品标价的9折优惠,故为实际价格.
∴(168+-500)×0.7+500×0.9=546.6元.
【变式训练】用固定的速度向如图形状的瓶子中注水,则水面的高度h和时间t之间的关系是( )
【解题指南】解答本题的关键是首先分清谁是自变量,谁是因变量,然后结合已知条件及瓶子的形状确定因变量与自变量的变化规律.
【解析】选B.由题可知随着时间的增加水面的高度增加得越来越快,因此选B.
5.【解析】(1)人的年龄与他拥有的财富之间存在依赖关系,但不是函数关系;(3)橘子的产量与气候之间存在依赖关系,但不是函数关系;(2)是函数关系.
答案:(1)(3)
6. 【解析】(1)此表反映的是变量音速随气温的变化;
(2)由表中数据可知,气温每升高5℃,音速加快3米/秒,又过点(0,331),故所求函数关系式为y=x+331.
(3)由(2)可知气温为22℃时音速y=×22+331,
故此人与燃放的烟花所在地约相距为5×(×22+331)=66+1 655=1 721米.
答案:(1)音速 气温 (2)y=x+331 (3)1 721
【误区警示】本题在求解(3)时常因把音速y错误地理解成距离而出错.
7. 【解析】(1)自行车出发较早,早3个小时,摩托车到达乙地较早,早3个小时.
(2)自行车:12.5千米/时;摩托车:50千米/时.
(3)自行车出发3~5小时内,两车均行驶在途中.①当3<x<4时,自行车行驶在摩托车前面;②当x=4时,自行车与摩托车相遇;③当4<x<5时,自行车行驶在摩托车后面.(其中x为自行车出发后经过的时间)
8.【解题指南】(1)根据x,y表示的意义以及函数的概念即可判定;
(2)根据表格即可直接写出;
(3)学生的接受能力最强,即y的值最大,即可确定对应的x值;
(4)根据表格可以得到y的值在未超过13分钟时越来越大,超过13分钟时越来越小,即可得解.
【解析】(1)反映了提出概念所用的时间x和对概念接受能力y两个变量之间的关系;其中x是自变量,y是因变量.
(2)由题中表格可知,当提出概念所用时间为10分钟时,学生接受能力是59.
(3)提出概念所用的时间为13分钟时,学生的接受能力最强.
(4)当x在2分钟至13分钟的范围内,学生的接受能力逐步增强;当x在13分钟至20分钟的范围内,学生的接受能力逐步降低.
【挑战能力】
【解析】(1)由图知,获得的金牌数y随着年份x的变化而变化,对于每一个x的值,都有唯一确定的一个y与它相对应,所以获得的金牌数y是年份x的函数.
由图知,金牌数16对应了年份1992和1996,即对于每一个y的值,并非都有唯一确定的一个x与它相对应,所以年份x不是获得的金牌数y的函数.
(2)从1996年开始由于中国每届奥运会金牌数都呈递增趋势且每届平均增长量超过10枚,由此推断中国2012年在伦敦奥运会上有望突破60枚金牌.
3.2 古典概型(第四、五课时)
3.2.1 —3.2.2古典概型及随机数的产生
一、教学目标:
1、知识与技能:(1)正确理解古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等;
(2)掌握古典概型的概率计算公式:P(A)=
(3)了解随机数的概念;
(4)利用计算机产生随机数,并能直接统计出频数与频率。
2、过程与方法:(1)通过对现实生活中具体的概率问题的探究,感知应用数学解决问题的方法,体会数学知识与现实世界的联系,培养逻辑推理能力;(2)通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯。
3、情感态度与价值观:通过数学与探究活动,体会理论来源于实践并应用于实践的辩证唯物主义观点.
二、重点与难点:1、正确理解掌握古典概型及其概率公式;2、正确理解随机数的概念,并能应用计算机产生随机数.
三、学法与教学用具:1、与学生共同探讨,应用数学解决现实问题;2、通过模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯.
四、教学设想:
1、创设情境:(1)掷一枚质地均匀的硬币,结果只有2个,即“正面朝上”或“反面朝上”,它们都是随机事件。
(2)一个盒子中有10个完全相同的球,分别标以号码1,2,3,…,10,从中任取一球,只有10种不同的结果,即标号为1,2,3…,10。
师生共同探讨:根据上述情况,你能发现它们有什么共同特点?
2、基本概念:
(1)基本事件、古典概率模型、随机数、伪随机数的概念见课本P121~126;
(2)古典概型的概率计算公式:P(A)=.
3、例题分析:
课本例题略
例1 掷一颗骰子,观察掷出的点数,求掷得奇数点的概率。
分析:掷骰子有6个基本事件,具有有限性和等可能性,因此是古典概型。
解:这个试验的基本事件共有6个,即(出现1点)、(出现2点)……、(出现6点)
所以基本事件数n=6,
事件A=(掷得奇数点)=(出现1点,出现3点,出现5点),
其包含的基本事件数m=3
所以,P(A)====0.5
小结:利用古典概型的计算公式时应注意两点:
(1)所有的基本事件必须是互斥的;
(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏。
例2 从含有两件正品a1,a2和一件次品b1的三件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率。
解:每次取出一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件有6个,即(a1,a2)和,(a1,b2),(a2,a1),(a2,b1),(b1,a1),(b2,a2)。其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产用A表示“取出的两种中,恰好有一件次品”这一事件,则
A=[(a1,b1),(a2,b1),(b1,a1),(b1,a2)]
事件A由4个基本事件组成,因而,P(A)==
例3 现有一批产品共有10件,其中8件为正品,2件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2)如果从中一次取3件,求3件都是正品的概率.
分析:(1)为返回抽样;(2)为不返回抽样.
解:(1)有放回地抽取3次,按抽取顺序(x,y,z)记录结果,则x,y,z都有10种可能,所以试验结果有10×10×10=103种;设事件A为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此,P(A)= =0.512.
(2)解法1:可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(x,y,z),则x有10种可能,y有9种可能,z有8种可能,所以试验的所有结果为10×9×8=720种.设事件B为“3件都是正品”,则事件B包含的基本事件总数为8×7×6=336, 所以P(B)= ≈0.467.
解法2:可以看作不放回3次无顺序抽样,先按抽取顺序(x,y,z)记录结果,则x有10种可能,y有9种可能,z有8种可能,但(x,y,z),(x,z,y),(y,x,z),(y,z,x),(z,x,y),(z,y,x),是相同的,所以试验的所有结果有10×9×8÷6=120,按同样的方法,事件B包含的基本事件个数为8×7×6÷6=56,因此P(B)= ≈0.467.
小结:关于不放回抽样,计算基本事件个数时,既可以看作是有顺序的,也可以看作是无顺序的,其结果是一样的,但不论选择哪一种方式,观察的角度必须一致,否则会导致错误.
例4 利用计算器产生10个1~100之间的取整数值的随机数。
解:具体操作如下:键入
反复操作10次即可得之
小结:利用计算器产生随机数,可以做随机模拟试验,在日常生活中,有着广泛的应用。
例5 某篮球爱好者,做投篮练习,假设其每次投篮命中的概率是40%,那么在连续三次投篮中,恰有两次投中的概率是多少?
分析:其投篮的可能结果有有限个,但是每个结果的出现不是等可能的,所以不能用古典概型的概率公式计算,我们用计算机或计算器做模拟试验可以模拟投篮命中的概率为40%。
解:我们通过设计模拟试验的方法来解决问题,利用计算机或计算器可以生产0到9之间的取整数值的随机数。
我们用1,2,3,4表示投中,用5,6,7,8,9,0表示未投中,这样可以体现投中的概率是40%。因为是投篮三次,所以每三个随机数作为一组。
例如:产生20组随机数:
812,932,569,683,271,989,730,537,925,
907,113,966,191,431,257,393,027,556.
这就相当于做了20次试验,在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两次投中,它们分别是812,932,271,191,393,即共有5个数,我们得到了三次投篮中恰有两次投中的概率近似为=25%。
小结:(1)利用计算机或计算器做随机模拟试验,可以解决非古典概型的概率的求解问题。
(2)对于上述试验,如果亲手做大量重复试验的话,花费的时间太多,因此利用计算机或计算器做随机模拟试验可以大大节省时间。
(3)随机函数RANDBETWEEN(a,b)产生从整数a到整数b的取整数值的随机数。
例6 你还知道哪些产生随机数的函数?请列举出来。
解:(1)每次按SHIFT RNA# 键都会产生一个0~1之间的随机数,而且出现0~1内任何一个数的可能性是相同的。
(2)还可以使用计算机软件来产生随机数,如Scilab中产生随机数的方法。Scilab中用rand()函数来产生0~1之间的随机数,每周用一次rand()函数,就产生一个随机数,如果要产生a~b之间的随机数,可以使用变换rand()*(b-a)+a得到.
4、课堂小结:本节主要研究了古典概型的概率求法,解题时要注意两点:
(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
(2)古典概型的解题步骤;
①求出总的基本事件数;
②求出事件A所包含的基本事件数,然后利用公式P(A)=
(3)随机数量具有广泛的应用,可以帮助我们安排和模拟一些试验,这样可以代替我们自己做大量重复试验,比如现在很多城市的重要考试采用产生随机数的方法把考生分配到各个考场中。
5、自我评价与课堂练习:
1.在40根纤维中,有12根的长度超过30mm,从中任取一根,取到长度超过30mm的纤维的概率是( )
A. B. C. D.以上都不对
2.盒中有10个铁钉,其中8个是合格的,2个是不合格的,从中任取一个恰为合格铁钉的概率是
A. B. C. D.
3.在大小相同的5个球中,2个是红球,3个是白球,若从中任取2个,则所取的2个球中至少有一个红球的概率是 。
4.抛掷2颗质地均匀的骰子,求点数和为8的概率。
5.利用计算器生产10个1到20之间的取整数值的随机数。
6.用0表示反面朝上,1表正面朝上,请用计算器做模拟掷硬币试验。
6、评价标准:
1.B[提示:在40根纤维中,有12根的长度超过30mm,即基本事件总数为40,且它们是等可能发生的,所求事件包含12个基本事件,故所求事件的概率为,因此选B.]
2.C[提示:(方法1)从盒中任取一个铁钉包含基本事件总数为10,其中抽到合格铁订(记为事件A)包含8个基本事件,所以,所求概率为P(A)==.(方法2)本题还可以用对立事件的概率公式求解,因为从盒中任取一个铁钉,取到合格品(记为事件A)与取到不合格品(记为事件B)恰为对立事件,因此,P(A)=1-P(B)=1-=.]
3.[提示;记大小相同的5个球分别为红1,红2,白1,白2,白3,则基本事件为:(红1,红2),(红1,白1),(红1,白2)(红1,白3),(红2,白3),共10个,其中至少有一个红球的事件包括7个基本事件,所以,所求事件的概率为.本题还可以利用“对立事件的概率和为1”来求解,对于求“至多”“至少”等事件的概率头问题,常采用间接法,即求其对立事件的概率P(A),然后利用P(A)1-P(A)求解]。
4.解:在抛掷2颗骰子的试验中,每颗骰子均可出现1点,2点,…,6点6种不同的结果,我们把两颗骰子标上记号1,2以便区分,由于1号骰子的一个结果,因此同时掷两颗骰子的结果共有6×6=36种,在上面的所有结果中,向上的点数之和为8的结果有(2,6),(3,5),(4,4),(5,3),(6,2)5种,所以,所求事件的概率为.
5.解:具体操作如下
键入
反复按 键10次即可得到。
6.解:具体操作如下:
键入
7、作业:根据情况安排
