19.3课题学习-选择方案课件 (共22张PPT)人教版八年级数学下册
文档属性
| 名称 | 19.3课题学习-选择方案课件 (共22张PPT)人教版八年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 21:23:21 | ||
图片预览






文档简介
(共22张PPT)
课题学习-选择方案
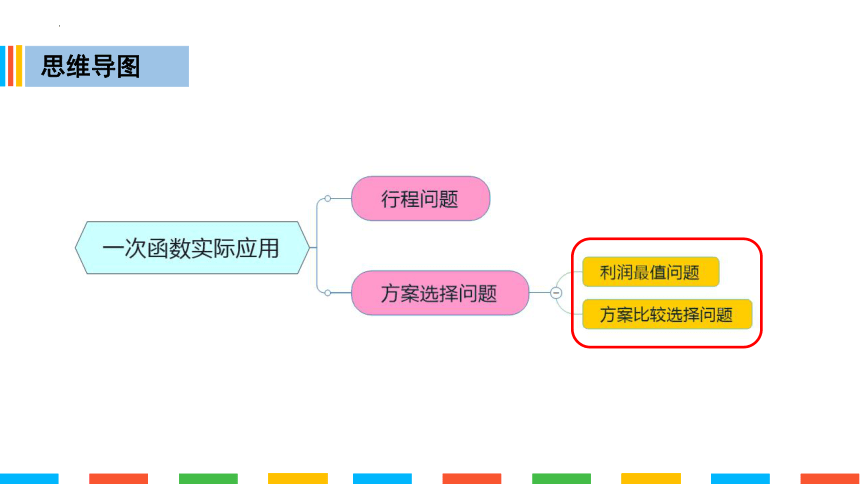
思维导图
课程目标
3.掌握利润最值问题的解题思路及解题技巧
4.体会分类讨论思想在一次函数实际问题中的应用
1.理解实际应用问题中的场景构建,会找其中的等量关系
2.掌握一次函数方案选择问题的解题思路及解题技巧
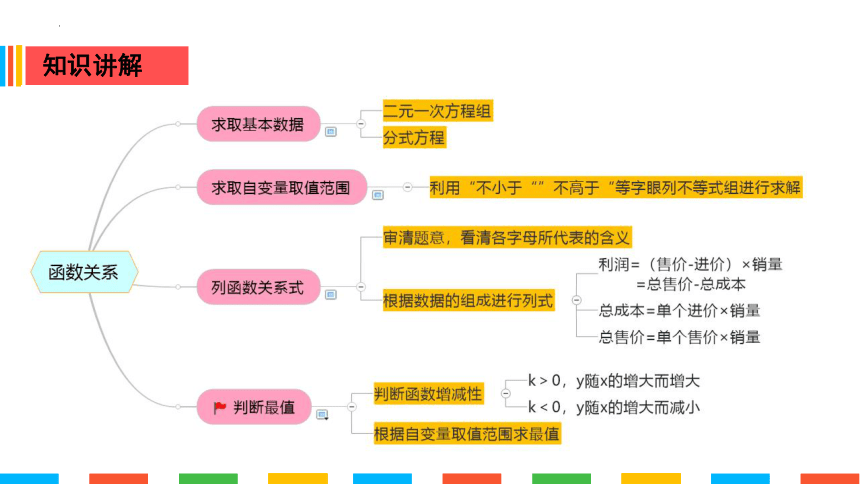
知识讲解
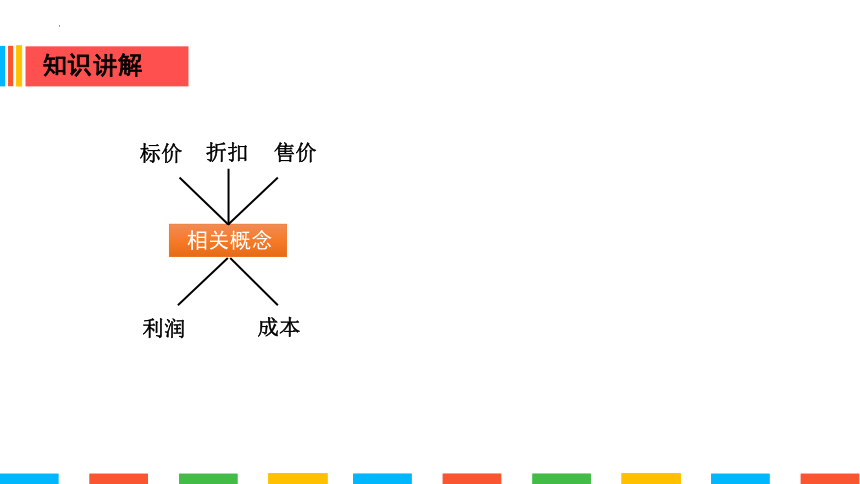
相关概念
成本
售价
利润
标价
折扣
知识讲解
例题讲解
某苹果生产基地,用名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利元,加工成罐头出售每吨获利元.采摘的工人每人可以采摘苹果吨,加工罐头的工人每人可加工苹果吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有名工人进行苹果采摘,罐头和苹果全部售出后,总利润为元.
(1)加工成罐头的苹果数量为________吨,直接出售的苹果数量为________吨.(用含的代数式表示)
例题讲解
某苹果生产基地,用名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利元,加工成罐头出售每吨获利元.采摘的工人每人可以采摘苹果吨,加工罐头的工人每人可加工苹果吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有名工人进行苹果采摘,罐头和苹果全部售出后,总利润为元.
(2)求与之间的函数关系式.
例题讲解
某苹果生产基地,用名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利元,加工成罐头出售每吨获利元.采摘的工人每人可以采摘苹果吨,加工罐头的工人每人可加工苹果吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有名工人进行苹果采摘,罐头和苹果全部售出后,总利润为元.
(3)求为何值时利润最大,并求出最大利润.
【答案】
(1)加工成罐头的苹果数量为:=(吨),直接出售的苹果数量为:=吨
故答案为:;;
(2)由题意可得:==;
(3)根据题意,得,解得,
∴ 的取值是的整数.
∵ =,
∴ 随的增大而减小.
∴ 当=时总利润最大,最大利润==(元).
例题讲解
应用练习
某营业厅销售部型号手机和部型号手机的营业额为元,销售部型号手机和部型号手机的营业额为元.
求每部型号手机和型号手机的售价;
该营业厅计划一次性购进两种型号手机共部,其中型号手机的进货数量不超过型号手机数量的倍.已知型手机和型手机的进货价格分别为元部和元部,设购进型号手机部,这部手机的销售总利润为元.
①求关于的函数关系式;
②该营业厅购进型号和型号手机各多少部时,才能使销售总利润最大,最大利润为多少元?
某街道积极响应垃圾分类号召,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买3个垃圾箱和2个温馨提示牌共需550元,垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)如果该街道至少需要安放垃圾箱48个,如果购买温馨提示牌和垃圾箱共100个,且购买费用不超过10000元,请列举出所有购买方案,并指出哪种方案的资金最少?最少需多少元?
应用练习
随着电动自行车的市场需求量日渐增多.某商店计划最多投入万元购进,两种型号的电动自行车共辆,其中每辆型电动自行车比每辆型电动自行车多元.用万元购进的型电动自行车数量与用万元购进的型电动自行车数量一样.
求,两种型号电动自行车的进货单价;
若型电动自行车每辆售价为元,型电动自行车每辆售价为元,设该商店计划购进型电动自行车辆,两种型号的电动自行车全部销售后可获利润元.写出与之间的函数关系式;
该商店如何进货才能获得最大利润?此时最大利润是多少元?
应用练习
课堂小结
知识讲解
例题讲解
工厂需要某一规格的纸箱个.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为元;
方案二:由工厂租赁机器加工制作.工厂需要一次性投入机器安装等费用元,每加工一个纸箱还需成本费元.
(1)请分别写出方案一的费用(元)和方案二的费用(元)关于(个)的函数关系式;
例题讲解
工厂需要某一规格的纸箱个.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为元;
方案二:由工厂租赁机器加工制作.工厂需要一次性投入机器安装等费用元,每加工一个纸箱还需成本费元.
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
【答案】
解:(1);;
(2)当时,即,解得;
当时,即,解得;
当时,即,解得.
∴ 当纸箱数量个时,选择方案一;
当纸箱数量个时,选择方案二;
当纸箱数量个时,选择两种方案都一样.
例题讲解
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按折收费;乙旅行社的优惠条件是:学生、家长都按折收费.假设这两位家长带领名学生去旅行,甲、乙旅行社的收费分别为,.
(1)写出、与的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
应用练习
“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过元后的价格部分打七折;乙店一次性购物中超过元后的价格部分打五折,设商品原价为元,购物应付金额为元.
(1)求在甲商店购物时与之间的函数关系;
(2)请写出“五一”期间选择哪家商店购物更优惠.
应用练习
应用练习
春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
租车公司:按日收取固定租金元,另外再按租车时间计费.共享汽车:无固定租金,直接以租车时间(时)计费.如图是两种租车方式所需费用(元)、(元)与租车时间(时)之间的函数图象,根据以上信息,回答下列问题:
(1)分别求出、与x的函数表达式;
(2)请你帮助小丽一家选择合算的租车方案.
“五 一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.根据以下信息,解答下列问题:
设租车时间为小时,租用甲公司的车所需费用为元,租用乙公司的车所需费用为元,分别求出,关于的函数表达式;
请你帮助小明计算并选择哪个出游方案合算.
应用练习
课堂大总结
课题学习-选择方案
思维导图
课程目标
3.掌握利润最值问题的解题思路及解题技巧
4.体会分类讨论思想在一次函数实际问题中的应用
1.理解实际应用问题中的场景构建,会找其中的等量关系
2.掌握一次函数方案选择问题的解题思路及解题技巧
知识讲解
相关概念
成本
售价
利润
标价
折扣
知识讲解
例题讲解
某苹果生产基地,用名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利元,加工成罐头出售每吨获利元.采摘的工人每人可以采摘苹果吨,加工罐头的工人每人可加工苹果吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有名工人进行苹果采摘,罐头和苹果全部售出后,总利润为元.
(1)加工成罐头的苹果数量为________吨,直接出售的苹果数量为________吨.(用含的代数式表示)
例题讲解
某苹果生产基地,用名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利元,加工成罐头出售每吨获利元.采摘的工人每人可以采摘苹果吨,加工罐头的工人每人可加工苹果吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有名工人进行苹果采摘,罐头和苹果全部售出后,总利润为元.
(2)求与之间的函数关系式.
例题讲解
某苹果生产基地,用名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利元,加工成罐头出售每吨获利元.采摘的工人每人可以采摘苹果吨,加工罐头的工人每人可加工苹果吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有名工人进行苹果采摘,罐头和苹果全部售出后,总利润为元.
(3)求为何值时利润最大,并求出最大利润.
【答案】
(1)加工成罐头的苹果数量为:=(吨),直接出售的苹果数量为:=吨
故答案为:;;
(2)由题意可得:==;
(3)根据题意,得,解得,
∴ 的取值是的整数.
∵ =,
∴ 随的增大而减小.
∴ 当=时总利润最大,最大利润==(元).
例题讲解
应用练习
某营业厅销售部型号手机和部型号手机的营业额为元,销售部型号手机和部型号手机的营业额为元.
求每部型号手机和型号手机的售价;
该营业厅计划一次性购进两种型号手机共部,其中型号手机的进货数量不超过型号手机数量的倍.已知型手机和型手机的进货价格分别为元部和元部,设购进型号手机部,这部手机的销售总利润为元.
①求关于的函数关系式;
②该营业厅购进型号和型号手机各多少部时,才能使销售总利润最大,最大利润为多少元?
某街道积极响应垃圾分类号召,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买3个垃圾箱和2个温馨提示牌共需550元,垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)如果该街道至少需要安放垃圾箱48个,如果购买温馨提示牌和垃圾箱共100个,且购买费用不超过10000元,请列举出所有购买方案,并指出哪种方案的资金最少?最少需多少元?
应用练习
随着电动自行车的市场需求量日渐增多.某商店计划最多投入万元购进,两种型号的电动自行车共辆,其中每辆型电动自行车比每辆型电动自行车多元.用万元购进的型电动自行车数量与用万元购进的型电动自行车数量一样.
求,两种型号电动自行车的进货单价;
若型电动自行车每辆售价为元,型电动自行车每辆售价为元,设该商店计划购进型电动自行车辆,两种型号的电动自行车全部销售后可获利润元.写出与之间的函数关系式;
该商店如何进货才能获得最大利润?此时最大利润是多少元?
应用练习
课堂小结
知识讲解
例题讲解
工厂需要某一规格的纸箱个.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为元;
方案二:由工厂租赁机器加工制作.工厂需要一次性投入机器安装等费用元,每加工一个纸箱还需成本费元.
(1)请分别写出方案一的费用(元)和方案二的费用(元)关于(个)的函数关系式;
例题讲解
工厂需要某一规格的纸箱个.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为元;
方案二:由工厂租赁机器加工制作.工厂需要一次性投入机器安装等费用元,每加工一个纸箱还需成本费元.
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
【答案】
解:(1);;
(2)当时,即,解得;
当时,即,解得;
当时,即,解得.
∴ 当纸箱数量个时,选择方案一;
当纸箱数量个时,选择方案二;
当纸箱数量个时,选择两种方案都一样.
例题讲解
暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按折收费;乙旅行社的优惠条件是:学生、家长都按折收费.假设这两位家长带领名学生去旅行,甲、乙旅行社的收费分别为,.
(1)写出、与的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
应用练习
“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过元后的价格部分打七折;乙店一次性购物中超过元后的价格部分打五折,设商品原价为元,购物应付金额为元.
(1)求在甲商店购物时与之间的函数关系;
(2)请写出“五一”期间选择哪家商店购物更优惠.
应用练习
应用练习
春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
租车公司:按日收取固定租金元,另外再按租车时间计费.共享汽车:无固定租金,直接以租车时间(时)计费.如图是两种租车方式所需费用(元)、(元)与租车时间(时)之间的函数图象,根据以上信息,回答下列问题:
(1)分别求出、与x的函数表达式;
(2)请你帮助小丽一家选择合算的租车方案.
“五 一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.根据以下信息,解答下列问题:
设租车时间为小时,租用甲公司的车所需费用为元,租用乙公司的车所需费用为元,分别求出,关于的函数表达式;
请你帮助小明计算并选择哪个出游方案合算.
应用练习
课堂大总结
