生活中的立体图形 [上学期]

课件32张PPT。第四章 图形的初步认识
第1节 生活中的立体图形

你已经认识了哪些立体图形？圆柱长方体正方体球体圆锥 我们已经认识的立体图形有： 生活中你会常见很多实物，由下列实物能想 象出你熟悉的几何体吗？
（1）文具盒
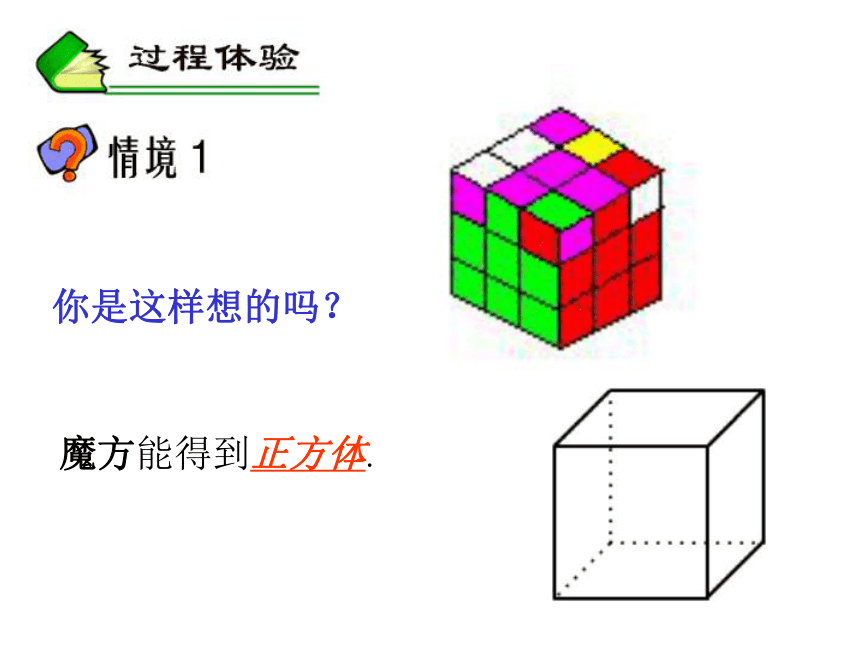
（2）魔方
( 3）笔筒
（4）足球
（5）漏斗你是这样想的吗？
文具盒能得到长方体 .魔方能得到正方体.你是这样想的吗？笔筒能得到圆柱体 .你是这样想的吗？漏斗能得到圆锥体.你是这样想的吗？足球能得到球体.你是这样想的吗？ 通过对你周边物体的观察、想象，归纳一下我们常见的几何体有哪些？ 正方体、长方体、棱柱、圆柱、圆锥、 棱锥、球等.请你想一想思考：长方体是柱体吗？正方形呢？ 由于它们的上下底面都是大小相等的平面图形,所以我们把它们归为一类叫做柱体 由于它们的顶端是尖的,所以我们把它们归为一类叫做锥体柱体 球体锥体圆柱棱柱圆锥棱锥由上、下两个底面和侧面组成。上、下底面一样大，是平面。由侧面和底面组成。（有明显的尖状）由球面组成。侧面是平面，且有明显的棱。底面是多边形。侧面是曲面，没有棱。底面是圆形。侧面是曲面，底面是圆形。侧面是三角形，有明显的棱，底面是多边形。 比较这些立体图形，看看相互之间有什么相似的地方，有什么不同的地方棱柱
( prism ) 圆柱
( circular cylinder ) 柱体
( cylinder )棱锥
( pyramid ) 圆锥
( circular cone )锥体
( cone )球体(sphere)柱体
( cylinder )锥体
( cone ) 球体
(sphere)三棱柱四棱柱五棱柱六棱柱可以按侧棱数或者底面的边数进行分类三棱锥四棱锥五棱锥六棱锥棱锥棱柱三棱柱四棱柱五棱柱六棱柱三棱锥四棱锥五棱锥六棱锥思考：圆柱有分为三圆柱、四圆柱……的吗？圆锥呢？（1）（2）（6）（5）（4）（3）你能说出下列图形的名称吗？（8）（7）三棱锥 圆柱四棱柱圆锥五棱锥五棱柱两圆柱的组合体斜切后的
圆柱体?



?
?
?
?
?
?

四面体六面体八面体十二面体二十面体多面体可以按面数来分类，如下列图形中： 认 识 多 面 体 围成立体图形的面是平的面，这样的立体图形又称为多面体 围成立体图形的面是平的面，这样的立体图形又称为多面体思考：圆是多面体吗？圆柱体呢？圆锥体呢？课后拓展 数一数下每一个多面体具有的顶点数(V)、棱数(E)和面数(F)，并且把结果记入表中. 861226812201230221220302欧拉公式：V+F-E=2 欧拉 (Euler，1707～1783) ， 伟大的瑞士数学家及自然科学家。
欧拉出生于牧师家庭，自幼受到父亲的教育。13岁时就入读巴塞尔大学，15岁大学毕业，16岁获得硕士学位。
他曾经因工作过度以致右眼失明。后来一场重病使他的左眼亦完全失明，但他以其惊人的毅力和心算技巧继续从事科学创作。他通过与助手们的讨论以及直接口授等方式完成了大量的科学着作，直至生命的最后一刻。
欧拉对数学的研究很广泛，因此在许多数学的分支中都能经常见到以他的名字命名的重要常数、公式和定理。 欧拉公式：
顶点数+面数－ 棱数=2找找看，你发现了哪些立体图形？巩固练习2. 写出下列立体图形的名称 :圆锥圆柱三棱锥三棱柱四棱柱圆柱巩固练习3、找出下面图形中的圆柱： BCDA巩固练习4、下面的图形表示四棱柱吗?你能说明理由吗? ABCDE巩固练习1、如图，第二行的图形围绕红线旋转一周，便能形成第一行的某个几何体，用线连一连. A B C D课堂小结本节课中，你知道了哪些立体图形？锥体柱体球体圆锥棱柱圆柱棱锥棱柱和棱锥怎样分类？多面体怎样分类？